
Jacob Steiner, geômetra berlinense do início do século 19definiu a tarefa de conectar três aldeias para que seu comprimento fosse o mais curto. Posteriormente, ele generalizou este problema: é necessário encontrar um ponto no plano de forma que a distância dele a n outros pontos seja a menor. No século 20, o trabalho continuou neste tópico. Decidiu-se pegar vários pontos e conectá-los de forma que a distância entre eles fosse a mais curta. Tudo isso é um caso especial do problema em estudo.
O algoritmo de Kruskal pertence aos algoritmos "gananciosos"(eles também são chamados de gradiente). A essência deles é a maior recompensa em cada etapa. Algoritmos gananciosos nem sempre fornecem a melhor solução para o problema. Existe uma teoria que mostra que, quando aplicados a problemas específicos, eles fornecem uma solução ótima. Esta é a teoria das matróides. O algoritmo de Kruskal pertence a tais problemas.
O algoritmo considerado constrói o ótimográfico wireframe. O problema é o seguinte. Você recebe um gráfico não direcionado sem arestas e loops múltiplos, e no conjunto de suas arestas, uma função de peso w é dada, que atribui a cada aresta e um número - o peso da aresta - w (e). O peso de cada subconjunto do conjunto de arestas é determinado pela soma dos pesos de suas arestas. É necessário encontrar o quadro com o menor peso.
O algoritmo de Kruskal funciona assim.Primeiro, todas as arestas do gráfico original são organizadas em ordem crescente de pesos. Inicialmente, o esqueleto não contém nenhuma aresta, mas inclui todos os vértices do gráfico. Após a próxima etapa do algoritmo, uma aresta é adicionada à parte já construída do esqueleto, que é uma floresta extensa. Não é escolhido arbitrariamente. Todas as arestas do gráfico que não pertencem ao wireframe podem ser chamadas de vermelho e verde. Os vértices de cada borda vermelha estão no mesmo componente de conectividade da floresta em construção, e os vértices da borda verde estão em diferentes. Portanto, se você adicionar uma borda vermelha lá, um ciclo aparecerá, e se for verde, o componente de conectividade na floresta obtido após esta etapa será um a menos. Assim, nenhuma borda vermelha pode ser adicionada à construção resultante, mas qualquer borda verde pode ser adicionada para criar uma floresta. E uma borda verde com peso mínimo é adicionada. O resultado é o quadro mais leve.
Vamos denotar a floresta atual F.Ele divide o conjunto de vértices do gráfico em áreas de conectividade (suas formas de união F, e eles não se cruzam em pares). As arestas vermelhas possuem ambos os vértices na mesma parte. A parte (x) é uma função que, para cada vértice x, retorna o nome da parte à qual x pertence. Unite (x, y) é um procedimento que constrói uma nova partição, consistindo na união das partes xey e todas as outras partes. Seja n o número de arestas do gráfico. Todos esses conceitos estão incluídos no algoritmo de Kruskal. Implementação:
Ordene todas as arestas do gráfico da 1ª à enésima ordem crescente de pesos. (ai, bi são os vértices da aresta com número i).
para i = 1 para n faça.
x: = Parte (ai).
y: = Parte (bi).
Se x não for igual ay, então Unite (x, y), inclua a aresta i em F.
Seja T o esqueleto do grafo original construído usando o algoritmo de Kruskal e S seu esqueleto arbitrário. Precisamos provar que w (T) não excede w (S).
Seja M o conjunto de arestas S, P seja o conjunto de arestasT. Se S não é igual a T, então há uma aresta et do quadro T que não pertence a S. Anexamos et a S. Um ciclo é formado, vamos chamá-lo de C. Removemos de C quaisquer arestas es pertencente a S. Temos um novo quadro, porque as bordas, e há tantos picos nele. Seu peso não excede w (S), pois w (et) é no máximo w (es) em virtude do algoritmo de Kruskal. Vamos repetir esta operação (substituindo as arestas S pelas arestas T) até obtermos T. O peso de cada quadro resultante subsequente não é maior que o peso do anterior, de onde segue que w (T) não é maior que w (S).
Além disso, a correção do algoritmo de Kruskal segue do teorema de Rado-Edmonds sobre matróides.
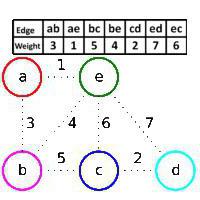
Dado um gráfico com vértices a, b, c, d, e e arestas (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Os pesos das costelas são mostrados na tabela e na figura. Inicialmente, a floresta F em construção contém todos os vértices do grafo e não contém nenhuma aresta. O algoritmo de Kruskal primeiro adiciona a aresta (a, e), uma vez que tem o menor peso, e os vértices a e e estão em diferentes componentes conectados da floresta F (a aresta (a, e) é verde), então a aresta ( c, d), portanto essa aresta tem o menor peso das arestas do gráfico que não pertence a F, e é verde, então a aresta (a, b) é adicionada pelos mesmos motivos. Mas a aresta (b, e) é ignorada, embora tenha o menor peso das arestas restantes, porque é vermelha: os vértices b e e pertencem ao mesmo componente conectado da floresta F, ou seja, se somarmos a aresta (b, e) para F, obtemos ciclo. Em seguida, uma borda verde (b, c) é adicionada, uma borda vermelha (c, e) é ignorada e, em seguida, d, e. Assim, as arestas (a, e), (c, d), (a, b), (b, c) são adicionadas sequencialmente. O esqueleto ideal do gráfico inicial consiste neles. É assim que o algoritmo funciona neste caso Pintado. Um exemplo mostra isso.

A figura mostra um gráfico que consiste em dois componentes conectados. As linhas em negrito mostram as bordas do wireframe ideal (verde) construído usando o algoritmo de Kruskal.

A figura superior mostra o gráfico original e a inferior mostra a estrutura de peso mínimo construída para ele usando o algoritmo considerado.
A sequência de arestas adicionadas: (1,6); (0,3), (2,6) ou (2,6), (0,3) - não importa; (3,4); (0,1), (1,6) ou (1,6), (0,1) também é indiferente (5,6).

O algoritmo de Kruskal encontra aplicação prática, por exemplo, para otimizar a implantação de comunicações, estradas em novos bairros de assentamentos de cada país, bem como em outros casos.


























