Binárne vzťahy a ich vlastnosti

Široká škála vzťahov, ako sú doložené množinamisprevádzané veľkým počtom konceptov, počnúc ich definíciami až po analytickú analýzu paradoxov. Rôznorodosť koncepcie, o ktorej sa hovorí v tomto článku, je na scéne nekonečná. Aj keď, keď hovoria o dvojakých typoch, znamenajú binárne vzťahy medzi niekoľkými množstvami. A tiež medzi objektmi alebo výrokmi.

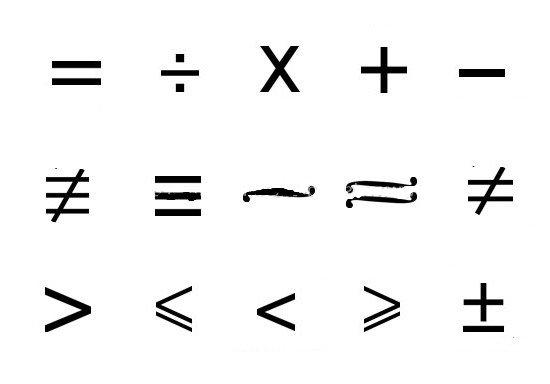
Typicky sú binárne vzťahy označenésymbol R, to znamená, že ak xRx pre ľubovoľnú hodnotu x z poľa R, takáto vlastnosť sa nazýva reflexívna, v ktorej x a x sú akceptované myšlienkové objekty a R slúži ako znak jedného alebo druhého druhu vzťahu medzi jednotlivcami . Zároveň, ak vyjadrujeme xRy® alebo yRx, znamená to stav symetrie, kde ® je implikačný znak, podobný spojke „if ..., then ...“ A nakoniec dekódovanie nápis (xRy Ùy Rz) ®xRz vám povie o prechodnom vzťahu a znak Ù je spojkou.

Binárny vzťah, ktorý sa vyskytuje súčasnereflexný, symetrický a tranzitívny, nazýva sa ekvivalenčný vzťah. Vzťah f je funkciou az Î a Î f vyplýva, že y = z. Jednoduchá binárna funkcia sa dá ľahko uplatniť na dva jednoduché argumenty v určitom poradí a iba v tomto prípade poskytuje hodnotu nasmerovanú na tieto dva výrazy v konkrétnom prípade.

Malo by sa povedať, že f mapy x až y,

Na základe vyššie uvedeného sú ekvivalenčné vzťahy binárnych vzťahov určené vlastnosťami:

• reflexivita - pomer (M ~ N);
• symetria - ak je rovnosť M ~ N, potom bude N ~ M;
• tranzitivita - ak dve rovnosti M ~ N a N ~ P, potom vo výsledku M ~ P.

Zvážte deklarované vlastnosti binárnych vzťahovpodrobnejšie. Reflexivita je jednou z charakteristík niektorých spojení, kde je každý prvok skúmanej množiny v danej rovnosti so sebou samým. Napríklad medzi číslami a = c a a³ c sú reflexné spojenia, pretože vždy a = a, c = c, a³ a, c³ c. Zároveň je nerovnostný vzťah a> c antireflexný z dôvodu nemožnosti existencie nerovnosti a> a. Axióma tejto vlastnosti je zakódovaná znakmi: aRc® aRa Ù cRc, kde symbol ® znamená slovo „znamená“ (alebo „implikuje“) a znak Ù - funguje ako spojka „a“ (alebo spojka). Z tohto tvrdenia vyplýva, že ak je rozsudok aRc pravdivý, sú pravdivé aj výrazy aRa a cRc.

Symetria znamená vzťaha v prípade, že sa mentálne objekty zamenia, to znamená so symetrickým vzťahom, permutácia predmetov nevedie k transformácii formy „binárne vzťahy“. Napríklad vzťah rovnosti a = c je symetrický kvôli ekvivalencii vzťahu c = a; rozsudok a1c je tiež rovnaký, pretože zodpovedá súvislosti s1a.

Prechodná množina je taká vlastnosť, prektorá spĺňa nasledujúcu požiadavku: y Î x, z Î y ® z Î x, kde ® je znamienko nahrádzajúce slová: „ak ..., potom ...“. Vzorec sa číta slovne takto: „Ak y závisí od x, z patrí y, potom z závisí aj od x.“