
ความสัมพันธ์ที่หลากหลายตามตัวอย่างของชุดพร้อมด้วยแนวคิดจำนวนมากเริ่มต้นด้วยคำจำกัดความและลงท้ายด้วยการวิเคราะห์เชิงวิเคราะห์เกี่ยวกับความขัดแย้ง ความหลากหลายของแนวคิดที่กล่าวถึงในบทความเกี่ยวกับชุดนั้นไม่มีที่สิ้นสุด แม้ว่าเมื่อพวกเขาพูดถึงสองประเภทพวกเขาหมายถึงความสัมพันธ์แบบไบนารีระหว่างปริมาณต่างๆ และระหว่างวัตถุหรือข้อความ
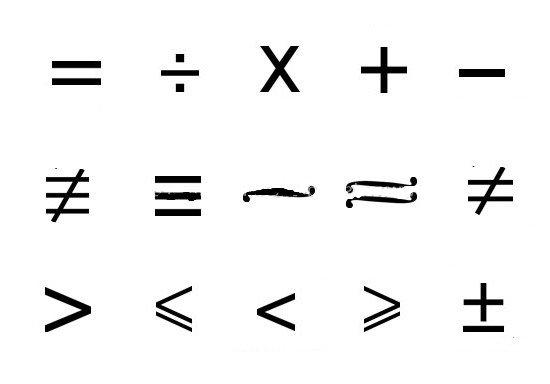
โดยปกติแล้วความสัมพันธ์แบบไบนารีจะแสดงสัญลักษณ์ R นั่นคือถ้า xRx สำหรับค่าใด ๆ x จากฟิลด์ R คุณสมบัติดังกล่าวเรียกว่ารีเฟล็กซีฟซึ่ง x และ x เป็นวัตถุแห่งความคิดที่ยอมรับและ R ทำหน้าที่เป็นสัญลักษณ์ของความสัมพันธ์แบบใดแบบหนึ่งระหว่างบุคคล . ในขณะเดียวกันถ้าเราแสดงxRy®หรือ yRx สิ่งนี้จะบ่งบอกถึงสถานะของสมมาตรโดยที่®เป็นเครื่องหมายแสดงนัยคล้ายกับการรวมกัน“ if ... , then ... ” และสุดท้ายการถอดรหัสของ คำจารึก (xRy Ùy Rz) ®xRzจะบอกคุณเกี่ยวกับความสัมพันธ์แบบสกรรมกริยาและเครื่องหมายÙคือการรวมกัน
ความสัมพันธ์แบบไบนารีที่เกิดขึ้นในเวลาเดียวกันรีเฟล็กซีฟสมมาตรและสกรรมกริยาเรียกว่าความสัมพันธ์ที่เท่าเทียมกัน ความสัมพันธ์ f คือฟังก์ชันและจาก <x, y> Î f และ <x, z> Î f จะเป็นไปตามนั้น y = z ฟังก์ชันไบนารีอย่างง่ายสามารถนำไปใช้กับอาร์กิวเมนต์ธรรมดาสองตัวในลำดับหนึ่ง ๆ ได้อย่างง่ายดายและในกรณีนี้เท่านั้นที่จะให้ความหมายที่นำไปยังนิพจน์ทั้งสองนี้ซึ่งนำมาใช้ในกรณีเฉพาะ
ควรจะบอกว่า f แม็พ x ถึง y

จากสิ่งที่กล่าวมาความสัมพันธ์ความเท่าเทียมกันของความสัมพันธ์ไบนารีถูกกำหนดโดยคุณสมบัติ:
พิจารณาคุณสมบัติที่ประกาศของความสัมพันธ์แบบไบนารีในรายละเอียดเพิ่มเติม การสะท้อนกลับเป็นหนึ่งในลักษณะเฉพาะของการเชื่อมต่อบางอย่างโดยที่แต่ละองค์ประกอบของชุดที่ตรวจสอบอยู่ในความเท่าเทียมกันที่กำหนดให้กับตัวมันเอง ตัวอย่างเช่นระหว่างตัวเลข a = c และa³ c คือการเชื่อมต่อแบบรีเฟลกซ์เพราะ a = a, c = c, a³ a, c³ c เสมอ ในเวลาเดียวกันความสัมพันธ์อสมการ a> c คือ antireflexive เนื่องจากความเป็นไปไม่ได้ของการดำรงอยู่ของอสมการ a> a สัจพจน์ของคุณสมบัตินี้ถูกเข้ารหัสด้วยเครื่องหมาย: aRc® aRa Ù cRc ในที่นี้สัญลักษณ์®หมายถึงคำว่า "entails" (หรือ "โดยนัย") และเครื่องหมายÙ - ทำหน้าที่เป็นสหภาพ "และ" (หรือตัวเชื่อม) ตามมาจากข้อความนี้ว่าถ้าการตัดสิน aRc เป็นจริงนิพจน์ aRa และ cRc ก็เป็นจริงเช่นกัน

สมมาตรก่อให้เกิดความสัมพันธ์และในกรณีที่วัตถุทางจิตมีการเปลี่ยนแปลงนั่นคือด้วยความสัมพันธ์แบบสมมาตรการเปลี่ยนรูปของวัตถุจะไม่นำไปสู่การเปลี่ยนแปลงรูปแบบ "ความสัมพันธ์แบบทวิภาค" ตัวอย่างเช่นความสัมพันธ์ของความเท่าเทียมกัน a = c เป็นแบบสมมาตรเนื่องจากความเท่ากันของความสัมพันธ์ c = a; การตัดสินa¹cก็เหมือนกันเนื่องจากสอดคล้องกับความสัมพันธ์กับ¹a
เซตสกรรมกริยาคือคุณสมบัติสำหรับซึ่งเป็นไปตามข้อกำหนดต่อไปนี้: y Î x, z Î y ® z Î x โดยที่®เป็นเครื่องหมายแทนที่คำว่า "if ... , then ... " สูตรจะอ่านด้วยวาจาดังนี้: "ถ้า y ขึ้นอยู่กับ x, z เป็นของ y ดังนั้น z ก็ขึ้นอยู่กับ x ด้วย"


























