
Значительное количество математических задач bilgi alanında dengesiz bir şekilde dağılmış bulguyla ilişkilidir. Coğrafi yönelime sahip bilgi sistemlerinden bahsediyoruz, çünkü belli noktalarda gerekli değerleri ölçmek mümkün. Bu sorunları çözmek için sıklıkla bir veya daha fazla enterpolasyon yöntemi kullanılır.

İnterpolasyon bir analizdirMevcut ayrık değerler kümesine göre değerlerin ara değerleri. En yaygın enterpolasyon yöntemleri şunlardır: ters ağırlıklı mesafeler, trend yüzeyi ve kriging yöntemi.
Öyleyse, ilk yönteme, özüne daha yakından bakalımdaha fazla bulunan noktalara kıyasla tahmini noktalara yakın noktaların etkisinden oluşur. Böyle bir enterpolasyon yöntemini kullanırken, belirli bir mahalledeki belirli bir topografiden, üzerinde en büyük etkiye sahip belirli bir noktayı seçmek gerekir. Bu, maksimum arama yarıçapını veya belirli bir noktaya yakın bulunan nokta sayısını seçer. Daha sonra ağırlık, bu noktadan uzaklığa bağlı olarak hesaplanan her bir noktadaki yükseklik için ayarlanır. Sadece bu şekilde, verilen noktadan daha uzak bir mesafedeki uzak noktalara kıyasla en yakın noktaların enterpolasyonlu yüksekliğe daha büyük bir katkısı elde edilebilir.
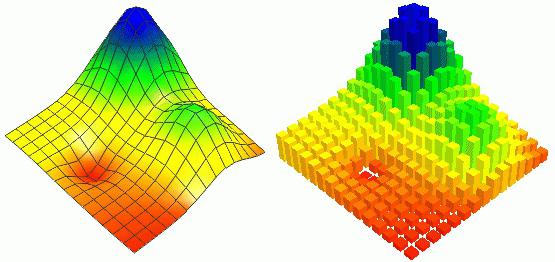

Существует еще один инструмент определения belirli noktalar - kuadratik enterpolasyon yöntemi, özü belirli bir aralıktaki bazı fonksiyonları kuadratik bir parabolle değiştirmektir. Ayrıca, ekstremumu analitik olarak hesaplanır. Yaklaşık konumundan (minimum veya maksimum) sonra, belirli bir değer aralığı ayarlamak gerekir, bundan sonra bir çözüm arayışı devam eder. Bu prosedürün tekrar gerçekleştirilmesi, tekrarlı bir prosedür kullanılarak, bu denklemin değerinin sonuca problemin ifadesinde belirtilen doğrulukla hassaslaştırılması mümkündür.


























