
Geometri kesin ve oldukça karmaşık bir bilimBütün bunlarla bir tür sanat. Çizgiler, uçaklar, oranlar - bütün bunlar gerçekten çok güzel şeyler yaratmanıza yardımcı olur. Ve garip bir şekilde, en çeşitli şekillerde ona dayanan geometridir. Bu yazıda, doğrudan bununla ilgili olan sıra dışı bir şeyi ele alacağız. Altın Oran tam olarak tartışılacak olan geometrik yaklaşımdır.
İnsanlar genellikle konunun şekline odaklanırMilyonlarca diğerleri arasında tanımak için. Önümüzde ne tür bir yalan olduğunu veya uzakta durduğumuzu belirliyoruz. Her şeyden önce insanları bedenleri ve yüzleri şeklinde tanıyoruz. Bu nedenle formun kendisinin, büyüklüğünün ve görünümünün insan algısındaki en önemli şeylerden biri olduğunu güvenle söyleyebiliriz.
İnsanlar için form her şeyi temsil ederiki ana sebepten dolayı ilgi: ya hayati bir zorunluluk tarafından belirlenir ya da güzellikten estetik zevkten kaynaklanır. En iyi görsel algı ve bir uyum ve güzellik duygusu, çoğu zaman bir insanın, simetri ve altın oran olarak adlandırılan özel bir oranın kullanıldığı bir form gördüğünde ortaya çıkar.
Yani altın oran altın orandır,Bu da harmonik bir bölünmedir. Bunu daha net açıklamak için formun bazı özelliklerini göz önünde bulundurun. Yani: form bir bütündür, ama sırayla bütün, her zaman bazı bölümlerden oluşur. Bu parçalar büyük olasılıkla farklı özelliklere, en azından farklı boyutlara sahiptir. Eh, bu boyutlar hem kendi aralarında hem de bütünsel olarak her zaman belirli bir orandadır.

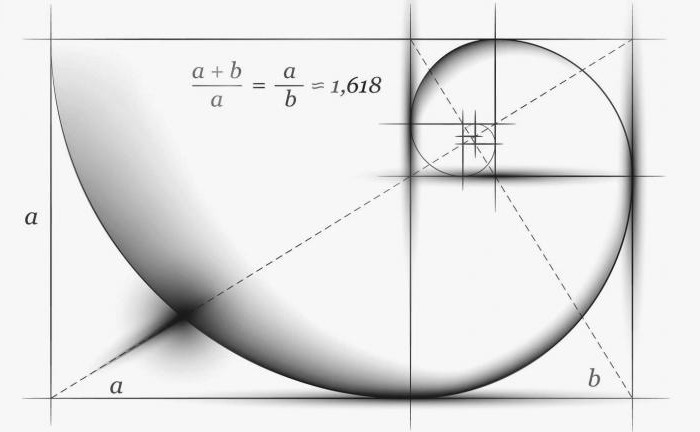
Yani başka bir deyişle, bunu savunabiliriz.altın oran, kendi formülüne sahip iki miktarın oranıdır. Formu oluşturmak için bu oranın kullanılması, insan gözü için olabildiğince güzel ve uyumlu olmasını sağlar.
Altın oran genellikleBugün hayatın en çeşitli yürüyüşleri. Fakat bu kavramın tarihi, matematik ve felsefe gibi bilimlerin henüz ortaya çıktığı eski zamanlara kadar uzanıyor. Bilimsel bir kavram olarak, altın oran Pisagor döneminde, yani, VI. Yüzyılda, ortaya çıktı. Fakat bundan önce bile, böyle bir oran bilgisi antik Mısır ve Babil'de pratikte kullanılıyordu. Bunun en somut kanıtı, sadece böyle altın bir oran kullandıkları için piramitlerdir.
Rönesans için yeni bir nefes olduharmonik bölünme, özellikle Leonardo da Vinci sayesinde. Bu oran hem geometri gibi hem de sanatta bilimlerde daha fazla kullanılmaya başlandı. Bilim adamları ve sanatçılar Altın Oran'ı daha derinden çalışmaya ve bu konuyla ilgilenen kitaplar yaratmaya başladılar.
En önemli tarihi eserlerden biri,Altın oranla ilişkili - bu, Luke Pancholi'nin "İlahi Orantılılık" adlı kitabı. Tarihçiler bu kitaptaki resimlerin Leonardo Vinci'nin kendisi tarafından yapıldığından şüpheleniyorlar.
Matematik çok net bir tanım verir.oranlar, bu iki oranın eşitliği olduğunu göstermektedir. Matematiksel olarak, bu aşağıdaki denklem ile ifade edilebilir: a: b = c: d, burada a, b, c, d bazı belirli değerlerdir.

Segmentin oranını iki bölüme ayırarak düşünürsek, sadece birkaç durumu karşılayabiliriz:
Altın oran gelince, o zaman bubir bölümün, büyük bölümün kendisi daha küçük olduğu için, bütün bölüm çoğunluğa karşılık geldiğinde, birbirine eşit olmayan bölümlere orantılı bölünmesi. Başka bir formülasyon daha var: daha küçük bir segment daha büyük bir bölüme, ayrıca tüm segment için daha büyük bir bölüme bağlı. Matematiksel terimlerle şöyle: a: b = b: c veya c: b = b: a. Bu tam olarak altın oran formülünün sahip olduğu şey.
Örnekleri olan altın bölümdüşünün, doğadaki inanılmaz fenomenleri ifade eder. Bunlar, matematiğin sadece sayılar ve formüller değil, doğada ve genel olarak hayatımızda gerçek bir yansımasından daha fazlasına sahip bir bilim olduğu gerçeğinin çok güzel örnekleridir.

Canlı organizmalar için ana yaşamdan birigörevler büyümedir. Aslında uzayda yerini alma arzusu aslında çeşitli şekillerde gerçekleştirilir - yukarı doğru büyüme, yere neredeyse yatay yayılma veya belirli bir destek üzerine spiralleme. Ve ne kadar inanılmaz olursa olsun, birçok bitki altın orana göre büyür.
Neredeyse inanılmaz bir başka gerçek de ilişkikertenkelelerin vücudunda. Vücutları insan gözü için yeterince güzel görünüyor ve bu aynı altın oran nedeniyle mümkün. Daha kesin olmak gerekirse, kuyruklarının uzunluğu tüm vücudun uzunluğunu 62: 38 olarak ifade eder.
Altın oran gerçekten inanılmaz bir kavram, yani tarih boyunca bu oran hakkında gerçekten ilginç gerçekleri karşılayabileceğimiz anlamına geliyor. Size bazılarını sunuyoruz:

Bu bölümde çok önemli olanlardan bahsetmek gerekir.kişi, yani S. Zeising. Bu, altın oranın araştırılmasında muazzam çalışmalar yapan bir Alman araştırmacıdır. Estetik Araştırma adlı bir eser yayınladı. Çalışmasında, altın oranı, hem doğadaki hem de sanattaki tüm fenomenler için evrensel olan mutlak bir kavram olarak sundu. Burada piramidin altın oranını ve insan vücudunun uyumlu oranını vb. Hatırlayabilirsiniz.
Zeising, altınlarınenine kesit aslında insan vücudu için ortalama istatistik yasasıdır. Bu pratikte gösterildi, çünkü çalışmaları sırasında birçok insan vücudunu ölçmek zorunda kaldı. Tarihçiler bu deneye iki binden fazla kişinin katıldığına inanıyorlar. Zeising araştırmasına göre, altın oranın ana göstergesi, vücudun göbek noktasına bölünmesidir. Dolayısıyla, ortalama 13: 8 oranına sahip erkek vücut, altın orana, altın oranın 8: 5 olduğu kadına göre biraz daha yakındır. Ayrıca, altın oran, örneğin el gibi vücudun diğer bölgelerinde de görülebilir.
Aslında, altın bir bölüm oluşturmak bir şeydirYeterince basit. Gördüğümüz gibi, eski insanlar bile bununla kolayca başa çıktı. İnsanlığın modern bilgi ve teknolojisi hakkında ne söylenir? Bu makalede, bunun sadece bir parça kağıda ve elinde bir kalemle nasıl yapılabileceğini göstermeyeceğiz, ancak bunun gerçekten mümkün olduğunu güvenle söyleyeceğiz. Dahası, bu birden fazla şekilde yapılabilir.
Bu oldukça basit bir geometri olduğundan,altın oranın okulda bile inşa edilmesi oldukça basittir. Bu nedenle, bu konudaki bilgiler özel kitaplarda kolayca bulunabilir. Altın oranı inceleyen Grade 6, yapısının ilkelerini tam olarak anlayabiliyor, bu da çocukların bile benzer bir görevi üstlenecek kadar akıllı oldukları anlamına geliyor.
Uygulamada altın oran ile ilk tanışma, aynı oranlarda düz bir çizgi segmentinin basit bir şekilde bölünmesiyle başlar. Çoğu zaman bu bir cetvel, pusula ve elbette bir kalemle yapılır.
Altın oranın parçaları şu şekilde ifade edilir:sonsuz irrasyonel fraksiyon AE = 0.618 ... AB bir birim olarak alınırsa, BE = 0.382 ... Bu hesaplamaları daha pratik hale getirmek için, çoğu zaman tam değil, yaklaşık değerler, yani 0.62 ve 0 kullanın, 38. AB segmenti 100 kısım için alınırsa, bunların çoğu sırasıyla 62, iyi ve daha küçük olacaktır - 38 kısım.

Altın oranın ana özelliği şu denklem ile ifade edilebilir: x2-x-1 = 0. Çözerken aşağıdaki kökleri elde ederiz: x1,2=. Matematik kesin ve titiz bir bilim olmasına rağmen, dalı geometri gibi, bu konuda gizem yaratan altın bölümün yasaları gibi özelliklerdir.
Özetlemek gerekirse, daha önce konuştuklarımızı kısaca ele alacağız.
Çoğunlukla altın oran kuralı altında3/8 ve 5/8'e yakın bir oranın gözlendiği birçok sanat örneği düşer. Bu ham altın oran formülüdür. Makale, bir bölüm kullanma örnekleri hakkında çoktan bahsetti, ancak antik ve modern sanatın prizmasıyla tekrar bakacağız. Yani, eski çağlardan en çarpıcı örnekler:

Muhtemelen bilinçli olarakorantı kullanımı, o zaman, Leonardo da Vinci zamanından beri, bilimden sanata, yaşamın hemen hemen tüm dallarında kullanılmaya başlandı. Biyoloji ve tıp bile altın oranın canlı sistemlerde ve organizmalarda bile çalıştığını kanıtlamıştır.


























