
Геометрія - це дуже багатогранна наука.Вона розвиває логіку, уяву та інтелект. Звичайно, через свою складність і величезної кількості теорем і аксіом, вона не завжди подобається школярам. Крім цього, існує необхідність постійно доводити свої висновки, використовуючи загальноприйняті стандарти і правила.

Освіта кутів
Будь-який кут утворюється шляхом перетину двохпрямих або проведення двох променів з однієї точки. Вони можуть називатися або однією літерою, або трьома, які послідовно позначають точки побудови кута.
Кути вимірюються в градусах і можуть (залежновід їх значення) по-різному називатися. Так, існує прямий кут, гострий, тупий і розгорнутий. Кожному з назв відповідає певна градусна міра або її проміжок.
Тупим є кут, що перевищує 90 градусів.
Кут називається прямим в тому випадку, коли його градусна міра дорівнює 90.
У тому випадку, коли він утворений однією суцільною прямою, і його градусна міра дорівнює 180, його називають розгорнутим.
суміжні кути
Кути, що мають спільну сторону, друга сторонаяких продовжує один одного, називаються суміжними. Вони можуть бути як гострими, так і тупими. Перетин розгорнутого кута лінією утворює суміжні кути. Властивості їх наступні:
Завдяки цим властивостям, можна завжди обчислити градусну міру кута, маючи значення іншого кута або, по крайней мере, ставлення між ними.

Кути, сторони яких є продовженням одна одної, називаються вертикальними. В якості такої пари можуть виступати будь-які їхні різновиди. Вертикальні кути завжди рівні між собою.
Вони утворюються при перетині прямих. Спільно з ними завжди присутні і суміжні кути. Кут може бути одночасно суміжних для одного і вертикальним для іншого.
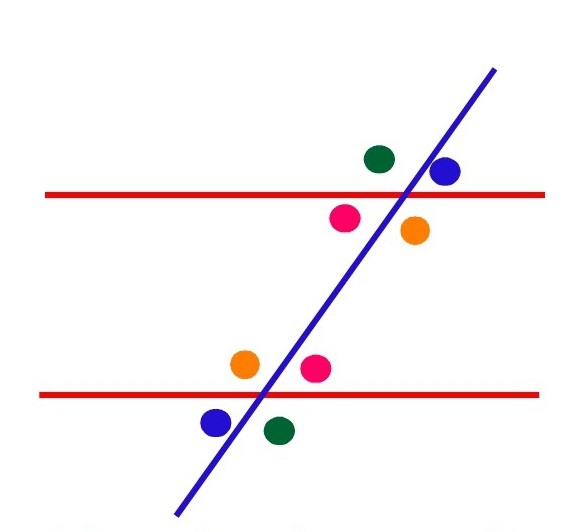
При перетині паралельних прямих довільноїлінією також розглядають ще кілька видів кутів. Така лінія називається січною, вона і утворює відповідні, односторонні і навхрест лежачі кути. Вони рівні між собою. Їх можна розглядати в світлі властивостей, які мають вертикальні і суміжні кути.
Таким чином, тема кутів представляється доситьпростою і зрозумілою. Всі їх властивості легко запам'ятати і довести. Рішення задач не буде складно доти, поки кутах відповідає числове значення. Вже далі, коли почнеться вивчення sin і cos, доведеться запам'ятовувати безліч складних формул, їх висновків і наслідків. А до того часу можна просто насолоджуватися легкими завданнями, в яких необхідно знайти суміжні кути.


























