Знаете ли какво означава "рационално" и кои числа се наричат ​​рационални?

В далеком прошлом, когда еще не была придумана система на изчисление, хората брои всичко на пръстите си. С навлизането на аритметиката и основите на математиката става много по-лесно и по-практично да се водят записи на стоки, продукти, както и на битови предмети. Как изглежда съвременното смятане? Какви видове съществуващи числа се разделят и какво означава "рационален вид числа"? Нека видим.

Колко разновидности на числата има в математиката?

Само понятие "число" обозначает некую единицу всеки предмет, който характеризира неговите количествени, сравнителни или порядъчни показатели. За да изчислите правилно броя на определени неща или да извършите някои математически операции с числа (добавете, умножете и т.н.), първо трябва да се запознаете с разновидностите на същите тези числа.

Така че съществуващите числа могат да бъдат разделени на следните категории:

1. Натуральные - это те числа, которыми мы броим броя на обектите (най-малкото положително цяло число е 1, логично е броят на положителните цели числа да е безкраен, тоест няма най-голямо положително цяло число). Наборът от естествени числа обикновено се обозначава с буквата N.
2. Числа.Всички естествени числа принадлежат на този набор и към него се добавят отрицателни стойности, включително числото "нула". Обозначението на множеството цели числа е написано под формата на латинската буква Z.
3. Рационалните числа са тези, които психическиможем да преобразуваме в дроб, числителят на който ще принадлежи на множеството цели числа, а знаменателят - на цели числа. По-долу ще анализираме по-подробно какво означава „рационално число“ и ще дадем няколко примера.
4. Реалните числа са набор, който включва всички рационални и ирационални числа. Този набор се обозначава с буквата R.
5. Сложните числа съдържат частистински и част от променливо число. Сложните числа се използват при решаването на различни кубични уравнения, които от своя страна могат да имат отрицателен израз във формулите под коренния знак (i²= -1).

Какво означава "рационално": анализираме

Ако тези номера, които ниеможе да се представи като обикновена фракция, оказва се, че всички положителни и отрицателни цели числа също са включени в набора от рационални. В крайна сметка всяко цяло число, например 3 или 15, може да бъде представено като дроб, където единицата е в знаменателя.

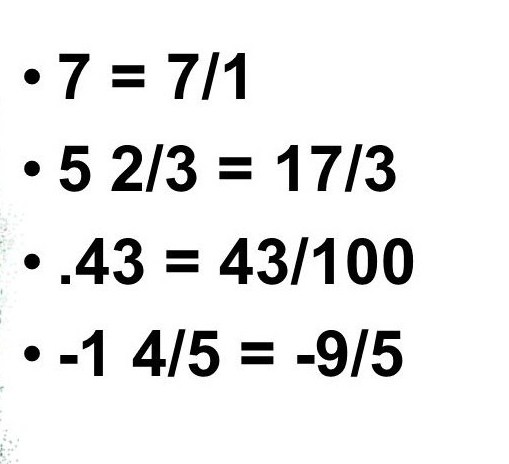
Фракции: -9/3; 7/5, 6/55 са примери за рационални числа.

Какво означава рационално изразяване?

Давай напред.Вече разбрахме какво означава рационалната форма на числата. Нека сега си представим математически израз, който се състои от сумата, разликата, произведението или коефициента на различни числа и променливи. Ето един пример: дроб, числителят на който е сборът от две или повече цели числа, а знаменателят съдържа едно цяло число и определена променлива. Този израз се нарича рационален. Въз основа на правилото „невъзможно е да се раздели на нула“, може да се предположи, че стойността на тази променлива не може да бъде такава, че стойността на знаменателя да стане нула. Следователно, когато решавате рационален израз, първо трябва да определите обхвата на променливата. Например, ако знаменателят има следния израз: x + 5-2, тогава се оказва, че "x" не може да бъде равно на -3. Всъщност, в този случай целият израз се превръща в нула, следователно при решаването е необходимо да се изключи целочисленото число -3 за тази променлива.

Как да решим рационални уравнения?

Рационалните изрази могат да съдържатдоста голям брой числа и дори 2 променливи, така че понякога решението им става трудно. За да се улесни решението на такъв израз, се препоръчва да се извършват определени операции по рационален начин. И така, какво означава "рационален начин" и какви правила трябва да се прилагат при вземането на решение?

1. Первый вид, когда достаточно всего лишь упростить изразяване. За целта можете да прибегнете до операцията по намаляване на числителя и знаменателя до неприводима стойност. Например, ако числителят има израза 18x, а знаменателят има 9x, тогава, намалявайки двата показателя с 9x, получаваме просто цяло число, равно на 2.
2. Вторият метод е практичен, когато имаме едночлен в числителя и полином в знаменателя. Нека вземем пример: в числителя имаме 5x, а в знаменателя - 5x + 20x², В този случай е най-добре да поставите променливатазнаменателя в скоби, получаваме следната форма на знаменателя: 5x (1 + 4x). И сега можете да използвате първото правило и да опростите израза, като намалите 5x в числителя и знаменателя. В резултат на това получаваме част от формата 1/1 + 4x.

Какви действия могат да бъдат извършени с рационални числа?

Множеството от рационални числа има своето числофункции. Много от тях са много подобни на характеристиката, присъстваща в цели числа и естествени числа, тъй като последните винаги са включени в много рационални числа. Ето няколко свойства на рационалните числа, като знаете кои лесно можете да разрешите всеки рационален израз.

1. Свойството за комутативност ви позволява да сумирате две или повече числа, независимо от реда им. Просто казано, сумата не се променя поради промяна на местата на условията.
2. Разпределителното свойство ни позволява да решаваме проблеми, използвайки закона за разпределение.
3. И накрая, операциите на събиране и изваждане.

Дори учениците знаят какво означава рационално.тип числа “и как да решим проблемите въз основа на такива изрази, така че възрастен образован човек просто трябва да запомни поне основите на много рационални числа.