
Nyní budeme hovořit o geometrické optice.V této části je hodně času věnováno takovému předmětu, jako je čočka. Koneckonců, může to být jiné. Současně je vzorec tenké čočky pro všechny případy stejný. Musíte jen vědět, jak ji správně použít.

Je to vždy tělo průhledné pro paprsky světla, které má zvláštní tvar. Vzhled objektu je diktován dvěma kulovými povrchy. Jeden z nich lze nahradit plochým.
Kromě toho může být čočka silnější uprostřed nebookraje. V prvním případě se bude nazývat konvexní, ve druhém - konkávní. Kromě toho v závislosti na tom, jak jsou konkávní, konvexní a ploché povrchy kombinovány, mohou být čočky také odlišné. Jmenovitě: bikonvexní a bikonvexní, rovinově konvexní a rovinově konkávní, konvexně konkávní a konkávně-konvexní.
В обычных условиях эти объекты используются в ve vzduchu. Jsou vyrobeny z látky, jejíž optická hustota je větší než u vzduchu. Proto se bude konvexní čočka shromažďovat a konkávní čočka se rozptyluje.
Než začnete mluvit tenká čočka vzorec, musíte se rozhodnout o základních pojmech. Musí být známí. Protože budou neustále řešeny různými úkoly.
Hlavní optická osa je rovná.Je protažen středy obou kulových povrchů a určuje umístění středu čočky. Existují další optické osy. Jsou nakresleny bodem, který je středem čočky, ale neobsahují středy kulových povrchů.
Ve vzorci tenké čočky je množství, které určuje její ohniskovou vzdálenost. Fokus je tedy bod na hlavní optické ose. V něm se paprsky protínají rovnoběžně se specifikovanou osou.
Kromě toho vždy existují dva triky pro každou tenkou čočku. Jsou umístěny na obou stranách jeho povrchů. Obě zaměření na sběratele jsou platné. V rozptylu - imaginární.
Vzdálenost od čočky k ohnisku je ohnisková vzdálenost (písmeno F).. Navíc může být jeho hodnota kladná (v případě sběru) nebo záporná (pro rozptyl).
Další charakteristika je spojena s ohniskovou vzdáleností - optickým výkonem. Je obvyklé to označovat D. Její hodnota je vždy vzájemným zaměřením, tj. D = 1 /F. Měřená optická energie v dioptriích (zkrácené dioptrie).
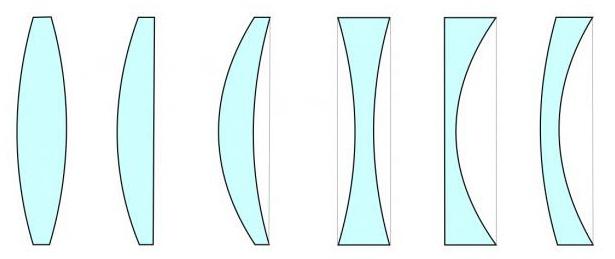
Kromě již zadané ohniskové vzdálenosti budete muset znát několik vzdáleností a velikostí. Pro všechny typy čoček jsou stejné a jsou uvedeny v tabulce.
| Označení | Název |
| d | vzdálenost k předmětu |
| x | výška studovaného předmětu |
| f | vzdálenost k obrázku |
| X | výška výsledného obrázku |
Všechny uvedené vzdálenosti a výšky se obvykle měří v metrech.
Ve fyzice je pojem zvětšení také spojen s formulací tenké čočky. Je definován jako poměr velikosti obrazu k výšce subjektu, tj. H / h. To může být označeno písmenem G.
Musíte to vědět, abyste získali vzorectenká čočka, sbírání nebo rozptyl. Výkres začíná skutečností, že obě čočky mají svůj vlastní schematický obrázek. Oba vypadají jako střih. Pouze ve sbírce na jeho koncích jsou šipky směřovány ven a v rozptylu - směrem od tohoto segmentu.
Nyní je nutné přitáhnout se k tomuto segmentukolmo k jeho středu. Zobrazí se hlavní optická osa. Na něm, na obou stranách čočky ve stejné vzdálenosti, se má zaznamenat trik.
Objekt, jehož obrázek chcete vytvořit, je nakreslen ve formě šipky. Ukazuje, kde je horní část položky. Obecně je objekt umístěn rovnoběžně s čočkou.
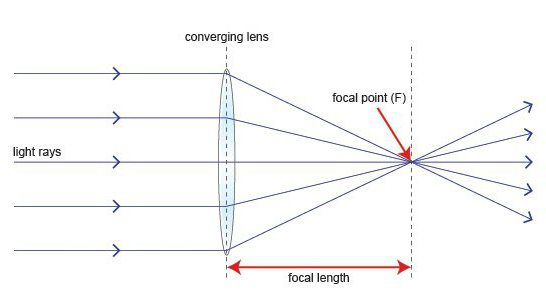
Chcete-li vytvořit obrázek objektu,jen najděte body konců obrázku a poté je spojte. Každý z těchto dvou bodů může být výsledkem průniku dvou paprsků. Nejjednodušší jsou dvě.
Přichází z určeného bodu rovnoběžně s hlavnímoptická osa. Po kontaktu s objektivem projde hlavním zaostřením. Pokud mluvíme o sběrné čočce, pak je toto zaostření za objektivem a paprsek jím projde. Při zvažování rozptylu musí být paprsek nakreslen tak, aby jeho pokračování prošlo zaostřením před čočkou.
Přímý průchod optickým středem objektivu. Po ní nemění svůj směr.
Jsou situace, kdy je položka doručenakolmo k hlavní optické ose a končí na ní. Pak stačí postavit obraz bodu, který odpovídá okraji šipky a neleží na ose. A pak z něj nakreslete kolmo k ose. Toto bude obraz předmětu.
Průsečík konstruovaných bodů dává obraz.V tenké sběrné čočce se získá skutečný obraz. To znamená, že se získává přímo na průniku paprsků. Výjimkou je situace, kdy je objekt umístěn mezi objektivem a zaostřením (jako v lupě), potom se obrázek ukáže jako imaginární. V rozptylu se vždy ukazuje, že je imaginární. Koneckonců, je získáváno na křižovatce ne samotných paprsků, ale jejich prodloužení.
Skutečný obrázek je obvykle nakreslen plnou čarou. Ale imaginární - tečkovaná čára. To je způsobeno skutečností, že první je tam skutečně přítomen a druhý je vidět pouze.
To se obvykle provádí na základě výkresu znázorňujícího konstrukci skutečného obrazu ve sběrné čočce. Označení segmentů je uvedeno na výkresu.
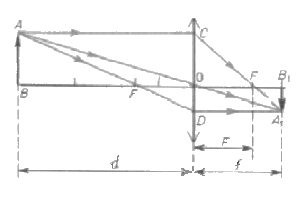
Sekce optiky není zbytečně nazývána geometrická. Bude to vzít znalosti z této části matematiky. Nejprve musíte zvážit trojúhelníky AOW a A1OV1. Jsou podobné, protože mají dva stejné úhly (rovný a svislý). Z jejich podobnosti vyplývá, že moduly segmentů A1V1 a AB označují jako moduly segmentů OB1 a OB.
Podobné (založené na stejném principu ve dvou úhlech) jsou další dva trojúhelníky: COF a A1FB1. V nich již stejné vztahy patří mezi takové moduly segmentů: A1V1 s CO a FB1s OF. Na základě konstrukce budou segmenty AB a CO stejné. Levé strany uvedených rovnic vztahů jsou tedy stejné. Právo je tedy stejné. To znamená, OB1 / S se rovná FB1/ OF.
V uvedené rovnosti mohou být segmenty označené tečkami nahrazeny odpovídajícími fyzickými pojmy. Takže ov1 Je vzdálenost od objektivu k obrázku. OB je vzdálenost od subjektu k objektivu. OF - ohnisková vzdálenost. Segment FB1 rovná rozdílu ve vzdálenosti k obrazu a zaostření. Proto ji lze přepsat jiným způsobem:
f / d = (f - F). / F nebo Ff = df - dF.
K odvození vzorce tenkých čoček je třeba rozdělit poslední rovnost dfF. Pak se ukáže:
1 / d + 1 / f = 1 / F.
Ten má vzorec tenké sběrné čočky.Rozptylová ohnisková vzdálenost je záporná. To vede ke změně rovnosti. Je pravda, že je to zanedbatelné. Právě ve vzorci tenké rozptylové čočky je před poměrem 1 mínus 1 /F. Tj:
1 / d + 1 / f = - 1 / F.
Stav. Ohnisková vzdálenost sběrné čočky je 0,26 m. Je-li subjekt ve vzdálenosti 30 cm, je třeba vypočítat jeho zvětšení.
Rozhodnutí. Začíná se zavedením zápisu a překladem jednotek do C. Dobře známý d = 30 cm = 0,3 ma F = 0,26 m. Nyní musíte vybrat vzorec, ten hlavní, který je určen pro zvětšení, druhý - pro tenkou sběrnou čočku.
Musí být nějakým způsobem kombinovány. Chcete-li to provést, budete muset zvážit kreslení obrázku v sběrné čočce. Z těchto trojúhelníků je zřejmé, že Γ = H / h= f / d. To znamená, že za účelem nalezení zvýšení je třeba vypočítat poměr vzdálenosti k obrázku a vzdálenosti k objektu.
Druhý je známý. Vzdálenost k obrázku by však měla být odvozena od vzorce uvedeného výše. Ukázalo se, že
f = df / (d - F).
Nyní je třeba tyto dva vzorce kombinovat.
R = df / (d(d - F)) = F / (d - F).
V tomto okamžiku řešení problému vzorce tenkých čoček přichází na elementární výpočty. Zbývá nahradit známá množství:
G = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Odpověď: objektiv dává zvětšení 6,5krát.

Stav. Lampa je umístěna jeden metr od sběrné čočky. Obraz jeho spirály se získá na obrazovce 25 cm od čočky Vypočítejte ohniskovou vzdálenost zadané čočky.
Řešení. Předpokládá se, že do dat zapíšeme následující hodnoty: d = 1 ma f = 25 cm = 0,25 m. Tato informace je dostatečná pro výpočet ohniskové vzdálenosti ze vzorce tenké čočky.
Takže 1 /F = 1/1 + 1 / 0,25 = 1 + 4 = 5. Ale v problému je nutné znát zaměření, nikoli optický výkon. Zbývá tedy pouze rozdělit 1 na 5 a získat ohniskovou vzdálenost:
F = 1/5 = 0,2 m
Odpověď: ohnisková vzdálenost sběrné čočky je 0,2 m.
Stav. Svíčka byla umístěna ve vzdálenosti 15 cm od sběrné čočky. Jeho optický výkon je 10 dioptrií. Obrazovka za objektivem je nastavena tak, aby vytvořila jasný obraz svíčky. K čemu je tato vzdálenost rovná?
Řešení. V krátkém záznamu se má psát následující data: d = 15 cm = 0,15 m, D = 10 dioptrií Výše uvedený vzorec musí být napsán s malou změnou. Konkrétně na pravou stranu rovnosti D místo 1 /F.
Po několika transformacích získáme následující vzorec pro vzdálenost od čočky k obrázku:
f = d / (dd - 1).
Nyní musíte nahradit všechna čísla a počítat. Ukazuje se tato hodnota pro F: 0,3 m
Odpověď: vzdálenost od objektivu k obrazovce je 0,3 m.

Stav. Objekt a jeho obraz jsou od sebe vzdáleny 11 cm. Sběrná čočka umožňuje trojnásobné zvětšení. Najděte její ohniskovou vzdálenost.
Řešení. Vzdálenost mezi objektem a jeho obrázkem je obvykle označena písmenem L = 72 cm = 0,72 m. Zvýšení G = 3.
Jsou zde možné dvě situace.Za prvé - objekt je za zaostřením, to znamená, že obraz je skutečný. Ve druhém je objekt mezi zaostřením a objektivem. Pak je obraz na stejné straně jako předmět a imaginární.
Zvažte první situaci. Objekt a snímek jsou na opačných stranách sběrné čočky. Zde můžete napsat následující vzorec: L = d + F. Druhá rovnice má psát: f / d. Systém těchto rovnic je třeba vyřešit dvěma neznámými. Chcete-li to provést, vyměňte L o 0,72 ma 3 o.
Z druhé rovnice se ukázalo, že f = 3d. Pak se první převede takto: 0,72 = 4d. Snadné počítání d = 0,18 (m). Nyní snadno na místě f = 0,54 (m).
Pro výpočet ohniskové vzdálenosti zůstává použití vzorce tenké čočky. F = (0,18 x 0,54) / (0,18 + 0,54) = 0,135 (m). Toto je odpověď na první případ.
Ve druhé situaci - obraz je imaginární a vzorec pro L bude jiné: L = f - d. Druhá rovnice pro systém bude stejná. Stejným způsobem to chápeme d = 0,36 (m) a f = 1,08 (m). Podobný výpočet ohniskové vzdálenosti poskytne následující výsledek: 0,54 (m).
Odpověď: ohnisková vzdálenost objektivu je 0,135 m nebo 0,54 m.
Cesta paprsků v tenké čočce je důležitápraktická aplikace geometrické optiky. Koneckonců se používají v mnoha zařízeních, od jednoduchého lupy po přesné mikroskopy a dalekohledy. Proto o nich musíte vědět.
Odvozené složení tenké čočky umožňuje řešenímnoho úkolů. Navíc vám umožňuje vyvodit závěry o tom, který obrázek dává různé typy objektivů. V tomto případě stačí znát jeho ohniskovou vzdálenost a vzdálenost k objektu.


























