
Berlin -geometer Jacob Steiner fra begyndelsen af 1800 -talletsætte opgaven med, hvordan man forbinder tre landsbyer, så deres længde var den korteste. Efterfølgende generaliserede han dette problem: det er påkrævet at finde et punkt på flyet, så afstanden fra det til n andre punkter er den mindste. I det 20. århundrede fortsatte arbejdet med dette emne. Det blev besluttet at tage flere punkter og forbinde dem på en sådan måde, at afstanden mellem dem var den korteste. Alt dette er et specielt tilfælde af det problem, der undersøges.
Kruskals algoritme tilhører de "grådige" algoritmer(de kaldes også gradient). Essensen i sådanne er den største gevinst ved hvert trin. Grådige algoritmer giver ikke altid den bedste løsning på problemet. Der er en teori, der viser, at når de anvendes på specifikke problemer, giver de en optimal løsning. Dette er teorien om matroider. Kruskals algoritme tilhører sådanne problemer.
Den betragtede algoritme konstruerer det optimalewireframe graf. Problemet med det er som følger. Du får en uorienteret graf uden flere kanter og sløjfer, og på sættet af dens kanter er der givet en vægtfunktion w, som tildeler hver kant e et tal - kantens vægt - w (e). Vægten af hvert delmængde ud fra kantsættet bestemmes af summen af kanternes vægte. Det er påkrævet at finde rammen med den mindste vægt.
Kruskals algoritme fungerer sådan.Først er alle kanterne på den originale graf arrangeret i stigende vægtrækkefølge. Oprindeligt indeholder skelettet ingen kanter, men inkluderer alle grafens hjørner. Efter algoritmens næste trin tilføjes en kant til den allerede konstruerede del af skelettet, som er en spændende skov. Det vælges ikke vilkårligt. Alle kanter af grafen, der ikke tilhører wireframe, kan kaldes rød og grøn. Hodepunkterne for hver rød kant er i den samme forbindelseskomponent i skoven under opførelse, og hjørnerne på den grønne kant er i forskellige. Derfor, hvis du tilføjer en rød kant der, vises en cyklus, og hvis den er grøn, vil forbindelseskomponenten i skoven opnået efter dette trin være en mindre. Der kan således ikke tilføjes nogen rød kant til den resulterende konstruktion, men enhver grøn kant kan tilføjes for at skabe en skov. Og en grøn kant med minimal vægt tilføjes. Resultatet er den letteste ramme.
Lad os betegne den nuværende skov F.Det opdeler sæt af hjørner i grafen i forbindelsesområder (deres forening former F, og de skærer ikke parvis). De røde kanter har begge hjørner i samme del. Del (x) er en funktion, der for hvert toppunkt x returnerer navnet på den del, som x tilhører. Unite (x, y) er en procedure, der bygger en ny partition, der består af foreningen af x- og y -delene og alle andre dele. Lad n være antallet af kanter i grafen. Alle disse begreber er inkluderet i Kruskals algoritme. Gennemførelse:
Ordne alle kanter af grafen fra 1. til n. I stigende vægtrækkefølge. (ai, bi er kantens hjørner med tallet i).
for i = 1 til n gør.
x: = Del (ai).
y: = Del (bi).
Hvis x ikke er lig med y, så Foren (x, y), inkluder kant i i F.
Lad T være skelettet af den originale graf konstrueret ved hjælp af Kruskal -algoritmen, og S være dets vilkårlige skelet. Vi skal bevise, at w (T) ikke overstiger w (S).
Lad M være sættet med kanter S, P være sættet med kanterT. Hvis S ikke er lig med T, er der en kant et af rammen T, der ikke tilhører S. Lad os slutte et til S. En cyklus dannes, lad os kalde den C. Vi fjerner enhver kant fra C es tilhørende S. Vi får en ny ramme, fordi kanterne, og der er lige så mange toppe i den. Dens vægt overstiger ikke w (S), da w (et) højst er w (es) i kraft af Kruskals algoritme. Vi vil gentage denne handling (udskiftning af kanterne S med kanterne T), indtil vi får T. Vægten af hver efterfølgende resulterende ramme er ikke større end vægten af den forrige, hvorfra det følger, at w (T) ikke er større end w (S).
Korrektheden af Kruskals algoritme følger også af Rado-Edmonds-sætningen om matroider.
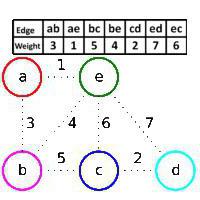
Givet en graf med hjørner a, b, c, d, e og kanter (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Ribbenes vægte er vist i tabellen og i figuren. Oprindeligt indeholder skoven F under opførelse alle kurvens hjørner og indeholder ingen kanter. Kruskals algoritme tilføjer først kanten (a, e), da den har den mindste vægt, og hjørnerne a og e er i forskellige forbundne komponenter i skoven F (kanten (a, e) er grøn), derefter kanten ( c, d), derfor at denne kant har den mindste vægt af de kanter af grafen, der ikke tilhører F, og den er grøn, så tilføjes kanten (a, b) af de samme årsager. Men kanten (b, e) springes over, selvom den har den mindste vægt af de resterende kanter, fordi den er rød: hjørnerne b og e tilhører den samme tilsluttede komponent i skoven F, det vil sige, hvis vi tilføjer kanten (b, e) til F, får vi cyklus. Derefter tilføjes en grøn kant (b, c), en rød kant (c, e) springes over, og derefter d, e. Således tilføjes kanterne (a, e), (c, d), (a, b), (b, c) sekventielt. Det optimale skelet i den indledende graf består af dem. Sådan fungerer algoritmen i dette tilfælde Malet. Et eksempel har vist dette.

Figuren viser en graf bestående af to tilsluttede komponenter. De fede linjer viser kanterne på den optimale wireframe (grøn) konstrueret ved hjælp af Kruskal -algoritmen.

Den øverste figur viser den originale graf, og den nederste viser den minimale vægtramme konstrueret til den ved hjælp af den betragtede algoritme.
Sekvensen af tilføjede kanter: (1,6); (0.3), (2.6) eller (2.6), (0.3) - er ligegyldigt; (3.4); (0,1), (1,6) eller (1,6), (0,1) er også ligegyldig (5,6).

Kruskals algoritme finder praktisk anvendelse, f.eks. Til at optimere kommunikationslægningen, veje i nye kvarterer i bosættelser i hvert land såvel som i andre tilfælde.


























