Spearmans korrelationskoefficient. Spearmans rang korrelationskoefficient

Disciplin "højere matematik" for nogleforårsager afvisning, da det virkelig ikke alle er givet til at forstå det. Men de, der er heldige nok til at studere dette emne og løse problemer ved hjælp af forskellige ligninger og koefficienter, kan prale af næsten fuldstændig viden om det. Inden for psykologisk videnskab er der ikke kun en humanitær orientering, men også visse formler og metoder til matematisk verifikation af den hypotese, der er fremført i løbet af forskningen. Til dette anvendes forskellige koefficienter.

Spearmans korrelationskoefficient

Dette er en almindelig måling pr. Definitionforbindelsen mellem to tegn. Koefficienten kaldes også den ikke-parametriske metode. Det viser linkstatistikker. Det vil sige, for eksempel ved vi, at aggression og irritabilitet hos et barn er forbundet, og korrelationskoefficienten for Spearmans rækker viser det statistiske matematiske forhold mellem disse to tegn.

Hvordan beregnes rangkoefficienten?

Naturligvis har alle matematiske definitioner eller størrelser deres egne formler, hvormed de beregnes. Spearmans korrelationskoefficient besidder det også. Hans formel er som følger:

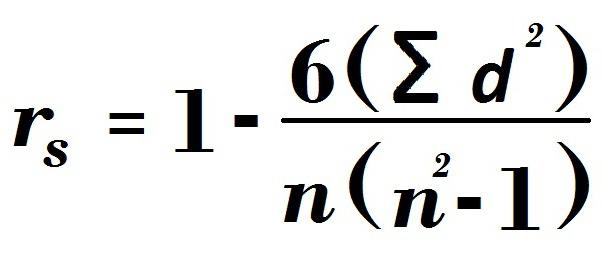
Ved første øjekast er formlen ikke helt klar, men hvis du finder ud af det, er alt meget let at beregne:

• n er antallet af funktioner eller indikatorer, der er rangeret.
• d er forskellen mellem de definerede to rækker svarende til de specifikke to variabler for hvert emne.
• ∑d^{2 -} summen af ​​alle firkanterne af forskellene i rækkerne af funktionen, hvis firkanter beregnes separat for hver rang.

Omfanget af det matematiske mål for kommunikation

For at anvende rangkoefficienten er det nødvendigtsåledes at de kvantitative data for karakteristikken blev rangeret, dvs. de blev tildelt et bestemt antal afhængigt af det sted, hvor karakteristikken er placeret, og på dens værdi. Det er bevist, at to serier af numeriske tegn er noget parallelle med hinanden. Spearmans rangkorrelationskoefficient bestemmer graden af ​​denne parallelitet, tætheden af ​​forbindelsen af ​​funktioner.

For at en matematisk operation kan beregne og bestemme forholdet mellem attributter ved hjælp af den specificerede koefficient, skal du udføre nogle handlinger:

1. Hver værdi af ethvert emne eller fænomen tildeles et nummer i rækkefølge - en rang. Det kan svare til fænomenets værdi i stigende og faldende rækkefølge.
2. Endvidere sammenlignes rækken af ​​værdierne for karakteristikaene for de to kvantitative serier for at bestemme forskellen mellem dem.
3. I en separat kolonne i tabellen, for hver opnået forskel, skrives dens firkant, og resultaterne opsummeres i bunden.
4. Efter disse handlinger anvendes formlen, hvormed Spearman-korrelationskoefficienten beregnes.

Korrelationskoefficientegenskaber

De vigtigste egenskaber ved Spearman-koefficienten inkluderer følgende:

• Måling af værdier i området fra -1 til 1.
• Koefficientens tegn har ingen fortolkninger.
• Forbindelsens tæthed bestemmes efter princippet: jo højere værdi, jo tættere er forbindelsen.

Hvordan kontrolleres den modtagne værdi?

For at kontrollere forbindelsen af ​​skilte med hinanden skal visse handlinger udføres:

1. En nulhypotese (H0) fremsættes, den er også den vigtigste, derefter en anden, alternativ til den første (H₁). Den første hypotese vil være, at Spearmans korrelationskoefficient er 0, hvilket betyder, at der ikke vil være noget forhold. Den anden, tværtimod, siger, at koefficienten ikke er lig med 0, så er der en forbindelse.
2. Det næste trin er at finde den observerede værdi af kriteriet. Det findes ved den grundlæggende formel for Spearman-koefficienten.
3. Dernæst de kritiske værdier for det givnekriterium. Dette kan kun gøres ved hjælp af en speciel tabel, der viser forskellige værdier for de angivne indikatorer: signifikansniveauet (l) og det antal, der bestemmer prøvestørrelsen (n).
4. Nu skal vi sammenligne de to opnåede værdier:etableret observerbar såvel som kritisk. For at gøre dette skal du opbygge et kritisk område. Det er nødvendigt at tegne en lige linje, markere punkterne for koefficientens kritiske værdi med et "-" tegn og med et "+" tegn. Til venstre og til højre for de kritiske værdier markerer halvcirkler fra punkterne de kritiske regioner. I midten, der kombinerer de to betydninger, er det markeret med en halvcirkel af OPG.
5. Derefter konkluderes der om forbindelsen mellem de to tegn er tæt.

Hvor er det bedre at bruge denne værdi

Den allerførste videnskab, hvor den blev brugt aktivtdenne koefficient var psykologi. Når alt kommer til alt er dette en videnskab, der ikke er baseret på tal, men for at bevise vigtige hypoteser om udvikling af relationer, karaktertræk hos mennesker, studerendes viden, statistisk bekræftelse af konklusionerne er påkrævet. Det bruges også i økonomien, især med valutaomsætning. Karakteristika uden statistik evalueres her. Spearmans rangkorrektionskoefficient er meget praktisk i dette anvendelsesområde, idet estimatet foretages uanset fordelingen af ​​variabler, da de erstattes af et rangnummer. Spearman-koefficienten bruges aktivt i bankvirksomhed. Sociologi, statskundskab, demografi og andre videnskaber bruger det også i deres forskning. Resultater opnås hurtigt og så præcist som muligt.

Spearmans korrelationskoefficient i Excel bruges bekvemt og hurtigt. Der er specielle funktioner her, der hjælper dig med hurtigt at få de værdier, du har brug for.

Hvilke andre korrelationskoefficienter er der?

Ud over hvad vi lærte om koefficientenSpearmans korrelationer, der er også forskellige korrelationskoefficienter, der gør det muligt at måle, evaluere kvalitative træk, forholdet mellem kvantitative træk, tætheden af ​​forholdet mellem dem, præsenteret i rangskalaen. Disse er koefficienter såsom bisserial, rang-bisserial, indhold, associationer osv. Spearmans koefficient viser meget nøjagtigt forbindelsens tæthed i modsætning til alle andre metoder til dets matematiske bestemmelse.