
Yksi tärkeimmistä tieteistä, jonka soveltaminen voinähdä matematiikan, kuten kemian, fysiikan ja jopa biologian aloilla. Tämän tieteen tutkimuksen avulla voit kehittää joitain henkisiä ominaisuuksia, parantaa abstraktia ajattelua ja keskittymiskykyä. Yksi matematiikan kurssilla erityistä huomiota ansaitsevista aiheista on murto-osien lisääminen ja vähentäminen. Monille opiskelijoille sen opiskelu on vaikeaa. Ehkä artikkelimme auttaa ymmärtämään tätä aihetta paremmin.
Дроби – это те же числа, с которыми можно suorittaa erilaisia toimia. Niiden ero kokonaislukuista on nimittäjän läsnäolo. Siksi suorittaessasi fraktioita koskevia toimia on tarpeen tutkia joitain niiden ominaisuuksista ja säännöistä. Yksinkertaisin tapaus on tavallisten murtojen vähentäminen, joiden nimittäjät on esitetty samalla numerolla. Suorita tämä toiminto ei ole vaikeaa, jos tiedät yksinkertaisen säännön:
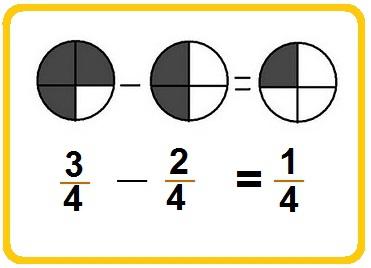
Katsotaan kuinka se näyttää esimerkistä:
7/19 - 3/19 = (7 - 3) / 19 = 4/19.
Vähennä jakson "7" osoittajavähennettävän murto-osan osoitin on "3", saamme "4". Me kirjoitamme tämän numeron vastauksen osoittimeen ja nimittäjään laitamme saman numeron, joka oli ensimmäisen ja toisen murto-osan nimittäjissä - "19".
Alla olevassa kuvassa on joitain samankaltaisia esimerkkejä.

Mieti monimutkaisempaa esimerkkiä, jossa vähennetään samojen nimittäjien fraktiot:
29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7) / 47 = i / 47.
Pelkistetyn jakeen "29" osoittimesta vähentämälläkaikkien seuraavien fraktioiden jononumerot - "3", "8", "2", "7". Tuloksena saadaan tulos "9", joka kirjoitetaan vastauksen osoittimeen, ja nimittäjään kirjoitetaan numero, joka on kaikkien näiden murtojen nimittäjissä - "47".
Tavallisten fraktioiden summaaminen ja vähentäminen suoritetaan saman periaatteen mukaisesti.
Katsotaan kuinka se näyttää esimerkistä:
1/4 + 2/4 = 3/4.
Murtoluvun ensimmäisen termin osoittajalle - "1" -lisää murto-osan toisen termin osoitin - "2". Tulos - "3" - kirjoitetaan summan osoittimeen, ja nimittäjä on sama kuin murto-osissa - "4".

Toimi fraktioilla, joilla on samanimittäjä, olemme jo pohtineet. Kuten näette, yksinkertaisten sääntöjen tunteminen on melko helppoa ratkaista tällaisia esimerkkejä. Mutta entä jos sinun täytyy suorittaa toiminto murto-osilla, joilla on eri nimittäjät? Nämä esimerkit ovat hämmentyneitä monista lukiolaisista. Mutta vaikka täällä tiedätkin ratkaisun periaatteen, esimerkit eivät enää ole sinulle vaikeita. Tässä on myös sääntö, jota ilman tällaisten fraktioiden ratkaisu on yksinkertaisesti mahdotonta.
Jos haluat vähentää murto-osia eri nimittäjillä, sinun on vietävä ne samaan alimpaan nimittäjään.

Puhumme lisää kuinka tämä tehdään.
Useiden fraktioiden tuomiseksisamalla nimittäjällä, sinun on käytettävä ratkaisussa olevan murto-osan pääominaisuutta: Kun olet jakanut tai kertannut osoittajan ja nimittäjän samalla numerolla, saat murto-osan, joka on annettu.
Joten esimerkiksi fraktiolla 2/3 voi olla sellainennimittäjät, kuten "6", "9", "12" jne., ts. se voi olla minkä tahansa numeron muodossa, joka on kerrannainen "3". Kun olemme kertoneet osoittajan ja nimittäjän luvulla "2", saadaan murto-osa 4/6. Kun kertomme alkuperäisen murto-osan osoittajan ja nimittäjän luvulla "3", saadaan 6/9, ja jos sama toimenpide suoritetaan numerolla "4", saadaan 8/12. Yhden tasa-arvon avulla se voidaan kirjoittaa näin:
2/3 = 4/6 = 6 / i = 8/12 ...
Mieti, kuinka vähentää useita fraktioitasama nimittäjä. Otetaan esimerkiksi alla olevan kuvan mukaiset fraktiot. Ensin on määritettävä, mistä numerosta voi tulla nimittäjä heille kaikille. Jotta se olisi helpompaa, otamme huomioon käytettävissä olevat nimittäjät.
Jakson 1/2 ja jakson 2/3 nimittäjä kertoimillasitä on mahdotonta hajottaa. Nimittäjällä 7/9 on kaksi tekijää 7/9 = 7 / (3 x 3), nimittäjän murto-osalla 5/6 = 5 / (2 x 3). Nyt on tarpeen määrittää, mitkä tekijät ovat pienimmät kaikille näille neljälle fraktiolle. Koska nimittäjän ensimmäinen fraktio sisältää luvun "2", mikä tarkoittaa, että sen on oltava läsnä kaikissa nimittäjissä, 7/9: n fraktiossa on kaksi triplettiä, mikä tarkoittaa, että molempien on oltava nimittäjään. Edellä esitetyn perusteella määritetään, että nimittäjä koostuu kolmesta tekijästä: 3, 2, 3 ja on yhtä suuri kuin 3 x 2 x 3 = 18.
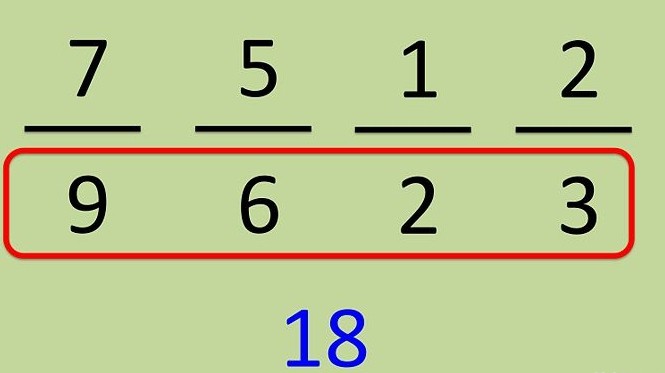
Рассмотрим первую дробь - 1/2.Sen nimittäjä sisältää "2", mutta ei ole yhtään numeroa "3", mutta niitä pitäisi olla kaksi. Tätä varten kerrotaan nimittäjä kahdella kolminkertaisella, mutta murto-ominaisuuden mukaan meidän on myös kerrottava osoittaja kahdella kolminkertaisella:
1/2 = (1 x 3 x 3) / (2 x 3 x 3) = 9/18.
Samoin suoritamme toimia jäljellä olevilla murto-osilla.
Yhdessä se näyttää tältä:

Kuten edellä mainittiin, jottaJos haluat lisätä tai vähentää murto-osia eri nimittäjillä, ne on pienennettävä samaan nimittäjään, ja sitten käyttää sääntöjä, joilla vähennetään fraktiot samasta nimittäjästä, jotka on jo kuvattu.
Katsotaanpa esimerkkiä: 4/18 - 3/15.
Löydä 18: n ja 15: n kerrannainen
Kun nimittäjä on löydetty,on tarpeen laskea tekijä, joka on erilainen kullekin murtoluvulle, eli luku, jolla on kerrottava nimittäjän lisäksi myös osoittaja. Tätä varten löydetty luku (yhteinen moninkertainen) jaetaan sen murto-osan nimittäjällä, jolle lisäkertoimet on määritettävä.
Seuraava ratkaisumme vaihe on tuoda kukin murto nimittäjälle "90".
Olemme jo keskustelleet siitä, miten tämä tehdään. Katsotaanpa, miten tämä on kirjoitettu esimerkkiin:
(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.
Jos murtoluvut ovat pieniä, yhteinen nimittäjä voidaan määrittää, kuten alla olevassa kuvassa.

Eri nimittäjillä varustettujen fraktioiden lisääminen suoritetaan samalla tavalla.
Olemme jo käsitelleet jakeiden vähennyksen ja niiden lisäämisen yksityiskohtaisesti. Mutta miten vähennät, jos murtoluvulla on kokonaislukuosa? Käytetään jälleen muutamia sääntöjä:

On toinenkin tapa, jolla voitsuorittaa kokonaisia osia sisältävien jakeiden lisäys ja vähentäminen Tätä varten toiminnot suoritetaan erikseen kokonaisilla osilla ja erikseen murtoluvuilla, ja tulokset kirjataan yhdessä.

Yllä oleva esimerkki koostuu murto-osista, jotkaon sama nimittäjä. Siinä tapauksessa, että nimittäjät ovat erilaisia, ne on vähennettävä samoiksi ja suoritettava toiminnot esimerkissä esitetyllä tavalla.
Toinen murtolukuisten toimintojen lajikkeistaon tapaus, jossa murtoluku on vähennettävä luonnollisesta luvusta. Ensi silmäyksellä tällainen esimerkki näyttää vaikealta ratkaista. Kaikki on kuitenkin täällä melko yksinkertaista. Sen ratkaisemiseksi on tarpeen muuntaa kokonaisluku murto-osaksi ja samalla nimittäjällä, joka on vähennettävässä osassa. Seuraavaksi teemme vähennyksen, samanlainen kuin vähennys, jolla on sama nimittäjä. Se näyttää esimerkiksi tältä:
7 - 4/9 = (7 x 9) / 9 - 4/9 = 53/9 - 4/9 = 49/9.
Murtolukujen vähennys (6luokka) on perusta monimutkaisempien esimerkkien ratkaisemiselle, joita käsitellään seuraavissa luokissa. Tämän aiheen tietoja käytetään myöhemmin ratkaisemaan funktioita, johdannaisia ja niin edelleen. Siksi on erittäin tärkeää ymmärtää ja ymmärtää yllä käsiteltyjä murto-osia.


























