
Étudier à l'école pour résoudre des équations en classemathématiciens, de nombreux étudiants sont souvent sûrs de perdre du temps, et pourtant une telle compétence est utile dans la vie non seulement à ceux qui décident de suivre les traces de Descartes, Euler ou Lobachevsky.
En pratique, comme la médecine ou l'économie,il arrive assez souvent qu'un spécialiste ait besoin de savoir quand la concentration de la substance active d'un médicament particulier atteint le niveau requis dans le sang du patient ou s'il est nécessaire de calculer le temps nécessaire à une entreprise particulière pour devenir rentable.
Le plus souvent, c'est une solution de non linéaireéquations de différents types. Pour ce faire le plus rapidement possible, notamment avec l'utilisation d'ordinateurs, autorisez les méthodes numériques. Ils sont bien étudiés et ont depuis longtemps prouvé leur efficacité. Parmi eux se trouve la méthode tangente de Newton, à laquelle cet article est consacré.

Dans ce cas, il existe une fonction g, qui est donnée sur l'intervalle (a, b) et y prend certaines valeurs, c'est-à-dire qu'il est possible pour chaque x appartenant à (a, b) d'associer un nombre spécifique g (x).
Il est nécessaire d'établir toutes les racines de l'équation à partir de l'intervalle entre les points a et b (y compris les extrémités) pour lesquels la fonction est mise à zéro. Évidemment, ce seront les points d'intersection de y = g (x) avec OX.
Dans certains cas, il est plus pratique de remplacer g (x) = 0 par un similaire de la forme g1(x) = g2(x). Dans ce cas, les racines sont les abscisses (valeur x) des points d'intersection des graphes g1(x) et g2(x).
Решение нелинейного уравнения важно и для задач optimisations pour lesquelles la condition d'un extremum local est une inversion de la dérivée de la fonction à 0. En d'autres termes, un tel problème peut être réduit à trouver les racines de l'équation p (x) = 0, où p (x) est identique à g "(x).
Pour certains types d'équations non linéaires,par exemple, trigonométrique carré ou simple, vous pouvez trouver les racines de manière assez simple. En particulier, chaque élève connaît les formules, à l'aide desquelles vous pouvez facilement trouver les valeurs d'argument des points où le trinôme carré est mis à zéro.
Méthodes d'extraction des racines d'équations non linéairesil est habituel de diviser en analytique (direct) et itératif. Dans le premier cas, la solution recherchée a la forme d'une formule, à l'aide de laquelle, dans un certain nombre d'opérations arithmétiques, on peut trouver la valeur des racines recherchées. Des méthodes similaires ont été développées pour les équations algébriques exponentielles, trigonométriques, logarithmiques et élémentaires. Pour le reste, vous devez utiliser des méthodes numériques spéciales. Ils sont faciles à mettre en œuvre à l'aide d'ordinateurs qui permettent de trouver les racines avec la précision requise.
Il s'agit notamment de la méthode dite de la tangente numérique. Cette dernière a été proposée par le grand scientifique Isaac Newton à la fin du XVIIe siècle. Au cours des siècles suivants, la méthode a été améliorée à plusieurs reprises.
Méthodes numériques pour résoudre des équations complexes, nonayant des solutions analytiques, il est accepté de réaliser en 2 étapes. Vous devez d'abord les localiser. Cette opération consiste à trouver de tels segments sur OX, sur lesquels il y a une racine de l'équation à résoudre.
Considérez le segment [a, b].Si g (x) n'a pas de discontinuités sur lui et prend des valeurs de signes opposés aux extrémités, alors entre a et b ou en eux il y a au moins 1 racine de l'équation g (x) = 0. Pour que ce soit unique, il faut que g (x) sur [a, b] soit monotone. Comme on le sait, il aura cette propriété à condition que g '(x) soit de signe constant.
En d'autres termes, si g (x) n'a pas de discontinuités sur [a, b] et augmente ou diminue de manière monotone, et que ses valeurs aux extrémités ont des signes différents, alors sur [a, b] il existe 1 et seulement 1 racine g (x).
Dans ce cas, sachez que ce critère ne s'appliquera pas aux racines des équations multiples.
Avant d'envisager des méthodes numériques plus complexes (méthode tangente et ses variétés) il vaut la peine de se familiariser avecle moyen le plus simple d'identifier les racines. Cela s'appelle la dichotomie et fait référence à des méthodes intuitives. L'algorithme pour trouver les racines est basé sur le théorème que si pour g (x) continue sur [x0, X1] la condition des différents signes est satisfaite, alors sur l'intervalle considéré il y a au moins 1 racine g (x) = 0.
Pour le trouver, vous devez diviser le segment [x0, X1] en deux et marquez le milieu comme x2... Ensuite, deux options sont possibles: g (x0) * g (x2) ou g (x2) * g (x1) sont égales ou inférieures à 0. Choisissez celle pour laquelle l'une de ces inégalités est vraie. Nous répétons la procédure ci-dessus jusqu'à ce que la longueur [x0, X1] ne deviendra pas inférieure à une certaine valeur présélectionnée qui détermine la précision de la détermination de la racine de l'équation sur [x0, X1u
Les avantages de la méthode comprennent sa fiabilité etsimplicité, et l'inconvénient est la nécessité d'identifier initialement les points auxquels g (x) prend des signes différents, de sorte qu'il ne peut pas être utilisé pour des racines avec une multiplicité égale. De plus, il ne peut pas être généralisé au cas d'un système d'équations ou lorsqu'il s'agit de racines complexes.
Supposons que nous voulions résoudre l'équation g (x) = 2x5 + x - 1 = 0.Afin de ne pas rechercher un segment approprié pendant une longue période, nous construisons un graphique en utilisant, par exemple, le programme Excel bien connu. On voit qu'il vaut mieux prendre des valeurs de l'intervalle [0,1] comme segment pour localiser la racine. Nous pouvons être sûrs qu'il y a au moins une racine de l'équation désirée dessus.
g "(x) = 10x4 + 1, c'est-à-dire qu'il s'agit d'une fonction à croissance monotone, il n'y a donc qu'une seule racine sur le segment sélectionné.
Remplacez les points de terminaison dans l'équation.Nous avons respectivement 0 et 1. À la première étape, nous prenons le point 0,5 pour la solution. Alors g (0,5) = -0,4375. Cela signifie que le prochain segment à diviser en deux sera [0,5, 1]. Son point médian est de 0,75. Dans celui-ci, la valeur de la fonction est de 0,226. Nous prenons en considération le segment [0,5, 0,75] et son milieu, qui est situé au point 0,625. Évaluez la valeur g (x) de 0,625. Il est égal à -0,11, ce qui est négatif. Sur la base de ce résultat, sélectionnez le segment [0,625, 0,75]. Nous obtenons x = 0,6875. Alors g (x) = -0,00532. Si la précision de la solution est de 0,01, nous pouvons supposer que le résultat souhaité est de 0,6875.
Cette méthode de recherche de racines à l'aide de la méthode tangente de Newton est populaire en raison de sa convergence très rapide.
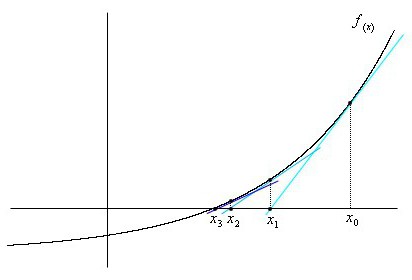
Il est basé sur le fait avéré que si xM. - approximation de la racine f (x) = 0 telle que f "C1, alors la prochaine approximation sera au point où l'équation de la tangente à f (x) s'annule, c'est-à-dire

Remplacer x = xn + 1 et définissez y à zéro.
Ensuite, l'algorithme de la méthode tangente ressemble à ceci:

Essayons d'utiliser la méthode classique de la tangente de Newton et trouvons une solution à une équation non linéaire difficile ou impossible à trouver analytiquement.
Qu'il soit nécessaire d'identifier les racines pour x3 + 4x - 3 = 0 avec une certaine précision, par exemple0,001. Comme vous le savez, le graphe de toute fonction sous la forme d'un polynôme de degré impair doit croiser l'axe OX au moins une fois, c'est-à-dire qu'il n'est pas nécessaire de douter de l'existence de racines.
Avant de résoudre notre exemple en utilisant la méthode tangente, nous construisons un graphe f (x) = x3 + 4x - 3 point par point. C'est très facile à faire, par exemple, en utilisant une feuille de calcul Excel. D'après le graphe résultant, on verra que sur [0,1] il intersecte l'axe OX et la fonction y = x3 + 4x - 3 augmente de manière monotone. On peut être sûr que sur [0,1] les équations x3 + 4x - 3 = 0 a une solution et c'est la seule.
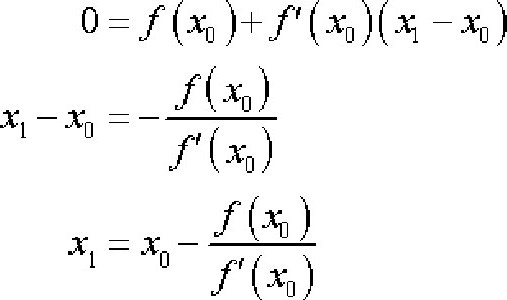
Toute solution d'équations par la méthode tangente commence par le calcul de f "(x). On a:
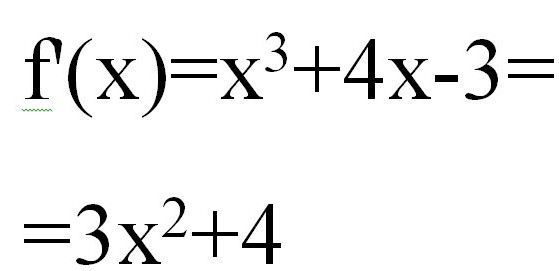
Ensuite, la deuxième dérivée aura la forme x * 6.
En utilisant ces expressions, nous pouvons écrire la formule pour identifier les racines de l'équation en utilisant la méthode tangente sous la forme:

Ensuite, vous devez choisir une approximation initiale, c'est-à-dire pour déterminer quel point est considéré comme le point de départ (ob.x0) pour le processus itératif. Considérons les extrémités du segment [0,1]. On convient à celui pour lequel la condition de la fonction et sa dérivée seconde en x0... Comme vous pouvez le voir, lors du remplacement de x0 = 0 il est violé, mais x0 = 1 c'est bien.
Comme

alors si on s'intéresse à la solution par la méthode des tangentes de précision e, alors la valeur xM. peut être considérée comme satisfaisant aux exigences du problème, à condition que l'inégalité | f (xM.) / f ’(xM.) | <e.
Lors de la première étape de résolution du problème par la méthode tangente, nous avons:

L'exemple précédent peut être résolu beaucoup plus facilement et plus rapidement si vous n'effectuez pas de calculs manuellement (sur une calculatrice), mais utilisez les capacités d'un processeur de feuille de calcul de Microsoft.
Pour ce faire, dans Excel, vous devez créer une nouvelle page et remplir ses cellules avec les formules suivantes:
Ensuite, vous devez "étirer" les formules des colonnes C, D et E, d'abord de deux lignes, et après que les valeurs y apparaissent, faites de même avec la colonne B.
Dans une tâche spécifique, déjà dans la cellule B10 apparaîtral'inscription "Achèvement des itérations", et pour résoudre le problème, vous devrez prendre le numéro écrit dans la cellule située une ligne au-dessus. Pour cela, vous pouvez sélectionner une colonne «extensible» distincte en y entrant une formule conditionnelle, selon laquelle le résultat y sera écrit si le contenu d'une cellule particulière de la colonne B prend la forme «Achèvement des itérations».
Essayons d'obtenir une solution à l'équation non linéaire y = x4 - 4 - 2 * x par la méthode tangente en Pascal.
Nous utilisons une fonction d'assistance quiaidera à effectuer un calcul approximatif de f "(x) = (f (x + delta) - f (x)) / delta. Comme condition pour l'achèvement du processus itératif, nous choisissons la réalisation de l'inégalité | X0-X1| <un petit nombre. En Pascal, nous l'écrivons comme abs (x0 - x1) <= epsilon.
Le programme est remarquable en ce qu'il ne nécessite pas de calcul manuel de la dérivée.

Envisagez une autre façon d'identifier les racineséquations non linéaires. Le processus d'itération consiste en ce que, comme approximations successives de la racine désirée pour f (x) = 0, les valeurs des points d'intersection de la corde avec les abscisses des extrémités a et b avec OX sont prises , noté x1, ..., XM. ... On a:
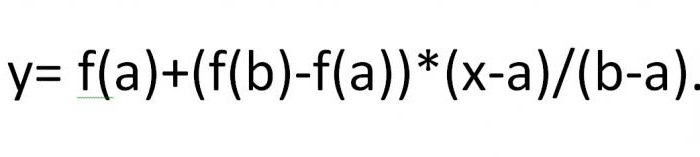
Pour le point d'intersection de la corde avec l'axe OX, l'expression s'écrira comme suit:

Soit la deuxième dérivée positive pour x £ [a, b] (le cas contraire sera réduit au cas considéré si on écrit - f (x) = 0). Dans ce cas, le graphe y = f (x) est une courbe convexe en bas et située sous la corde UN B... Il peut y avoir 2 cas: lorsque la fonction a une valeur positive au point a ou elle est négative au point b.
Dans le premier cas, nous choisissons la fin a comme fixe, et pour x0 prenez le point b. Ensuite, des approximations successives par la formule présentée ci-dessus forment une séquence qui décroît de manière monotone.
Dans le second cas, l'extrémité fixe est b en x0 = a. Les valeurs x obtenues à chaque étape d'itération forment une séquence qui augmente de manière monotone.
Ainsi, nous pouvons affirmer que:
Les itérations peuvent être poursuivies jusqu'à ce que les conditions de proximité des racines à cette étape et à l'étape d'itération précédente soient satisfaites modulo abs (xm - Xm - 1) <e.
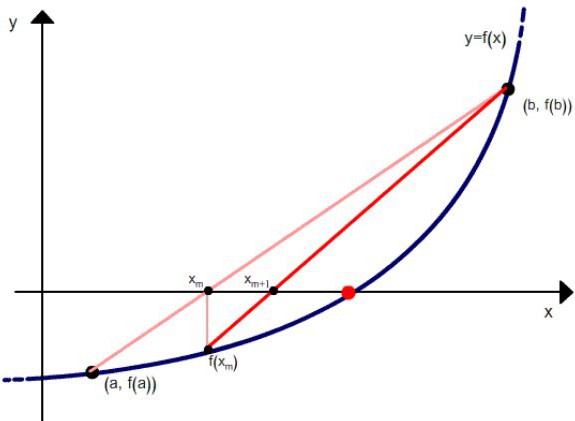
Méthode combinée des accords et des tangentes permet d'établir les racines de l'équation,les approcher de différents côtés. Une telle valeur, à laquelle le graphe f (x) croise OX, permet d'affiner la solution beaucoup plus rapidement que pour chacune des méthodes séparément.
Supposons que vous ayez besoin de trouver les racines f (x) = 0 siils sont sur [a, b]. Vous pouvez appliquer l'une des méthodes décrites ci-dessus. Cependant, il est préférable d'essayer une combinaison des deux, ce qui augmentera considérablement la précision de la racine.
Nous considérons le cas avec une approximation initiale correspondant à la condition que les dérivées première et seconde aient des signes différents en un point x particulier.
Dans ces conditions, la résolution d'équations non linéaires par la méthode tangente permet de trouver une racine avec un excès si x0= b, et la méthode utilisant des accords avec une extrémité fixe b conduit à trouver une racine approximative avec un déficit.
Les formules sont utilisées:

Maintenant, la racine requise x doit être recherchée dans l'intervalle [a1, b1]. L'étape suivante consiste à appliquer déjà la méthode combinée à ce segment. En agissant ainsi, nous obtenons des formules de la forme:

Si la différence de signes des dérivées première et seconde a lieu, alors, en argumentant de la même manière, pour affiner la racine, nous obtenons les formules récursives suivantes:

En tant que condition, l'inégalité estimée | bM.+1 - uneM.+1| <e. En d'autres termes, dans la pratique, vous devez trouver une solution en utilisant deux méthodes, mais à chaque étape, vous devez savoir à quel point les résultats sont proches les uns des autres.
Si l'inégalité ci-dessus est vraie, alors danscomme racine d'une équation non linéaire sur un segment donné, nous prenons un point qui est exactement au milieu entre les solutions trouvées à une étape d'itération particulière.
La méthode combinée est facilement implémentée dans l'environnement TURBO PASCAL. Si vous le souhaitez, vous pouvez essayer d'effectuer tous les calculs en utilisant la méthode tabulaire dans le programme Excel.
Dans ce dernier cas, plusieurs colonnes sont sélectionnées pour résoudre le problème à l'aide d'accords et séparément pour la méthode proposée par Isaac Newton.
Dans ce cas, chaque ligne est utilisée pour écrirecalculs à une étape d'itération spécifique par deux méthodes. Ensuite, à gauche de la zone de solution, sur la page de travail active, une colonne est mise en surbrillance, dans laquelle le résultat du calcul du module de la différence entre les valeurs de l'étape itérative suivante pour chacune des méthodes est entré. Un autre peut être utilisé pour saisir les résultats des calculs selon la formule de calcul de la structure logique "IF", qui permet de savoir si une condition est satisfaite ou non.
Vous savez maintenant comment résoudre des équations complexes. Méthode tangente, comme vous l'avez déjà vu, il est assez simple à mettre en œuvre, à la fois en Pascal et dans Excel. Par conséquent, vous pouvez toujours établir les racines d'une équation difficile ou impossible à résoudre à l'aide de formules.


























