
Povijest Pitagorina teorema ima nekolikotisućljeća. Tvrdnja da je kvadrat hipotenuze jednak zbroju kvadrata nogu, bila je poznata mnogo prije rođenja grčkog matematičara. Međutim, Pitagorejski teorem, povijest stvaranja i dokazi o njemu povezani su s većinom s ovim znanstvenikom. Prema nekim izvorima, razlog za to bio je prvi dokaz teorema, koji je dao Pitagora. Međutim, neki istraživači opovrgavaju tu činjenicu.

Prije nego što sam ispričao kako je priča napravljenaPitagorini teoremi, ukratko ćemo pregledati biografiju matematike. Živio je u VI stoljeću prije Krista. Datum rođenja Pitagore je 570 godina prije Krista. e., mjesto - otok Samos. O životu znanstvenika pouzdano je malo poznato. Biografski podaci u drevnim grčkim izvorima isprepleteni su s očitom fikcijom. Na stranicama rasprava on se pojavljuje kao veliki mudrac, vrhunski posjedujući riječ i sposobnost uvjeravanja. Usput, zato je grčka matematika nazvana Pitagora, tj. "Uvjerljiv govor". Prema drugoj verziji, budući mudrac je predvidio Pythia. Otac je nazvao dječaka Pitagoru u njezinu čast.

Mudrac je naučio iz velikih umova tog vremena.Među učiteljima mladih Pitagore su Germodesmant i Ferekid od Syrosa. Prvi je u njega usadio ljubav prema glazbi, drugu filozofiju. Obje ove znanosti će ostati u središtu pozornosti znanstvenika tijekom njegova života.
Prema jednoj verziji, biti radoznao mladić,Pitagora je otišao od kuće. Otišao je tražiti znanje u Egipat, gdje je ostao, prema različitim izvorima, od 11 do 22 godine, a zatim je zarobljen i poslan u Babilon. Pitagora je imao koristi od svog položaja. 12 godina studirao je matematiku, geometriju i magiju u drevnoj državi. Pitagora se vratio u Samos tek u dobi od 56 godina. Ovdje je u to vrijeme vladao tiranin Policrates. Pitagora nije mogao prihvatiti takav politički sustav i ubrzo je otišao na jug Italije, gdje se nalazila grčka kolonija Croton.
Danas je nemoguće sa sigurnošću reći je li Pitagora u Egiptu i Babilonu. Možda je kasnije ostavio Samosa i odmah otišao u Croton.

Povijest Pitagorina teorema povezana je s razvojemstvorila je grčka filozofska škola. Ovo religijsko i etičko bratstvo propovijedalo je poštivanje određenog načina života, proučavalo aritmetiku, geometriju i astronomiju, te proučavalo filozofsku i mističnu stranu brojeva.
Sva otkrića učenika grčkog matematičaranjemu se pripisuje. Međutim, povijest nastanka pitagorejskog teorema drevni biografi povezuju samo sa samim filozofom. Pretpostavlja se da je Grcima prenio znanje stečeno u Babilonu i Egiptu. Postoji i verzija da je doista otkrio teorem o omjeru nogu i hipotenuze, ne znajući za postignuća drugih naroda.
U nekim starogrčkim izvorimaopisuje Pitagorinu radost kad je uspio dokazati teorem. U čast takvog događaja naredio je žrtvovanje bogovima u obliku stotina bikova i priredio gozbu. Neki znanstvenici, međutim, ukazuju na nemogućnost takvog djela zbog osobitosti stavova pitagorejaca.
Vjeruje se da je u raspravi "Počeci", stvorenojEuklid, autor daje dokaz teorema, čiji je autor bio veliki grčki matematičar. Međutim, nisu svi podržali ovo stajalište. Primjerice, drevni neoplatonistički filozof Proklo naglasio je da je autor dokaza danih u Elementima sam Euclid.
Bilo kako bilo, ali Pitagora nije bio prvi koji je formulirao teorem.

Pitagorin teorem, čija je povijest stvaranjarazmatran u članku, prema njemačkom matematičaru Cantoru, bio je poznat već 2300. pr. e. u Egiptu. Drevni stanovnici doline Nila za vrijeme vladavine faraona Amenemhata znao sam jednakost 32 + 4² = 5²... Pretpostavlja se da su korištenjem trokuta sa stranama 3, 4 i 5 egipatska "potezanja užeta" izgrađena pod pravim kutom.
Znali su Pitegorin teorem u Babilonu.Glinene ploče iz 2000. godine pr i pripisan vladavini kralja Hammurabija, pronađen je približni izračun hipotenuze pravokutnog trokuta.
Povijest Pitagorinog teorema povezana je sa starimacivilizacije Indije i Kine. Rasprava "Zhou-bi Xuan Jin" sadrži naznake da je egipatski trokut (njegove su stranice u korelaciji 3: 4: 5) bio poznat u Kini već u 12. stoljeću. PRIJE KRISTA e., a do VI stoljeća. PRIJE KRISTA e. matematičari ove države znali su opći oblik teorema.
Konstrukcija pravog kuta pomoću egipatskog trokuta također je opisana u indijskoj raspravi "Sulva Sutra", koja datira iz 7.-5. Stoljeća. PRIJE KRISTA e.
Dakle, povijest pitagorejskog teorema u vrijeme rođenja grčkog matematičara i filozofa bila je stara već nekoliko stotina godina.
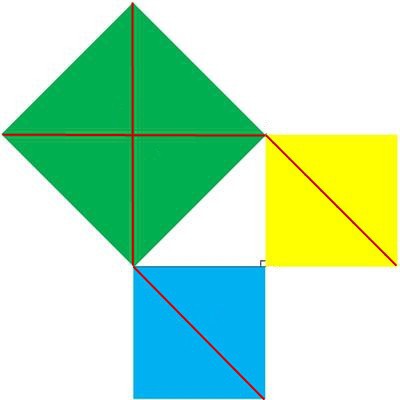
Tijekom svog postojanja teorem je postao jedantemeljnih u geometriji. Povijest dokaza Pitagorinog teorema vjerojatno je započela razmatranjem jednakostraničnog pravokutnog trokuta. Kvadrati su izgrađeni na njegovoj hipotenuzi i nogama. Onaj koji je "narastao" na hipotenuzi sastojat će se od četiri trokuta jednaka prvom. U ovom se slučaju kvadrati na nogama sastoje od dva takva trokuta. Jednostavan grafički prikaz jasno pokazuje valjanost izjave formulirane u obliku poznatog teorema.
Još jedan jednostavan dokaz kombinacijageometrija s algebrom. Četiri identična pravokutna trokuta sa stranicama a, b, c nacrtana su tako da tvore dva kvadrata: vanjski sa stranicom (a + b) i unutarnji sa stranicom c. U tom će slučaju površina manjeg kvadrata biti jednaka2... Površina velikog izračunava se iz zbroja površina malog kvadrata i svih trokuta (površina pravokutnog trokuta, podsjetimo, izračunava se formulom (a * b) / 2), odnosno sa2 + 4 * ((a * b) / 2), što je jednako c2 + 2av. Površina velikog kvadrata može se izračunati na drugi način - kao umnožak dviju stranica, tj. (A + b)2, što je jednako a2 + 2av + b2... Ispada:
i2 + 2av + b2 = sa2 + 2av,
i2 + u2 = sa2.
Postoji mnogo načina da se to dokažeteoremi. Na njima su radili i Euclid, indijski znanstvenici i Leonardo da Vinci. Drevni mudraci često su navodili crteže čiji su primjeri smješteni gore i nisu ih popratili nikakvim objašnjenjima, osim napomene "Pogledaj!" Jednostavnost geometrijskog dokaza, pod uvjetom da je bilo dostupno neko znanje, nije zahtijevala komentare.
Povijest Pitagorinog teorema, sažeta učlanak, razotkriva mit o njegovom nastanku. Međutim, teško je čak i zamisliti da će se ime velikog grčkog matematičara i filozofa jednog dana prestati povezivati s njom.


























