
Učenje u školi za rješavanje jednadžbi u razredumatematičari, mnogi su učenici često sigurni da troše vrijeme, a ipak je takva vještina korisna u životu ne samo onima koji se odluče slijediti Descartesa, Eulera ili Lobachevskog.
U praksi, poput medicine ili ekonomije,vrlo često postoje situacije kada specijalista mora otkriti kada koncentracija aktivne tvari određenog lijeka dosegne potrebnu razinu u pacijentovoj krvi ili je potrebno izračunati vrijeme potrebno za određenu djelatnost kako bi postala profitabilna.
Najčešće je to rješenje nelinearnojednadžbe raznih vrsta. Da biste to učinili što je brže moguće, posebno uz upotrebu računala, dopuštajte numeričke metode. Dobro su proučavani i odavno se pokazalo učinkovitim. Među njima je i Newton tangenta metoda kojoj je ovaj članak posvećen.

U ovom slučaju postoji funkcija g koja je dana na intervalu (a, b) i na njoj uzima određene vrijednosti, to jest, moguće je da svaki x koji pripada (a, b) može povezati određeni broj g (x).
Potrebno je uspostaviti sve korijene jednadžbe iz intervala između točaka a i b (uključujući krajeve) za koje je funkcija nula. Očito će to biti točke sjecišta y = g (x) s OX.
U nekim je slučajevima prikladnije g (x) = 0 zamijeniti sličnim oblikom g1(x) = g2(x). U ovom slučaju, apscise (x vrijednost) presječnih točaka grafova g1(x) i g2(x).
Rješavanje nelinearne jednadžbe također je važno za problemeoptimizacije za koje je uvjet lokalnog ekstrema da derivat funkcije nestane. Drugim riječima, takav se problem može svesti na pronalaženje korijena jednadžbe p (x) = 0, gdje je p (x) identičan g "(x).
Za neke vrste nelinearnih jednadžbi,na primjer, kvadratni ili jednostavni trigonometrijski, korijene možete pronaći na prilično jednostavne načine. Svaki student posebno zna formule pomoću kojih se lako mogu pronaći vrijednosti argumenta točaka u kojima je kvadratni trinom nuliran.
Metode za izdvajanje korijena nelinearnih jednadžbiuobičajeno je dijeliti se na analitičke (izravne) i iterativne. U prvom slučaju, željeno rješenje ima oblik formule, pomoću koje se u određenom broju aritmetičkih operacija može pronaći vrijednost željenih korijena. Slične metode razvijene su za eksponencijalne, trigonometrijske, logaritamske i osnovne algebarske jednadžbe. Za ostalo morate koristiti posebne numeričke metode. Lako ih je implementirati pomoću računala koja omogućuju pronalaženje korijena s potrebnom točnošću.
To uključuje takozvanu numeričku metodu tangente. Potonje je predlagao veliki znanstvenik Isaac Newton krajem 17. stoljeća. U sljedećim stoljećima metoda je nekoliko puta poboljšana.
Numeričke metode za rješavanje složenih jednadžbi, neimajući analitička rješenja, prihvaćeno je provoditi u 2 faze. Prvo ih trebate lokalizirati. Ova se operacija sastoji u pronalaženju takvih segmenata na OX, na kojima postoji jedan korijen jednadžbe koja se rješava.
Razmotrimo segment [a, b].Ako g (x) nema diskontinuiteta i poprima vrijednosti suprotnih predznaka na krajnjim točkama, tada se najmanje 1 korijen jednadžbe g (x) = 0 nalazi između a i b ili u njima samima. biti jedinstveni, potrebno je da je g (x) na [a, b] monotono. Kao što znate, imat će ovo svojstvo pod uvjetom da je g '(x) konstanta u znaku.
Drugim riječima, ako na [a, b] g (x) nema diskontinuiteta i monotono se povećava ili smanjuje, a njegove vrijednosti na krajnjim točkama imaju različite znakove, tada na [a, b] postoji 1 i samo 1 korijen g (x).
Istodobno, trebali biste biti svjesni da se ovaj kriterij neće primjenjivati na korijene jednadžbi koje su višestruke.
Prije razmatranja složenijih numeričkih metoda (tangentna metoda i njegove sorte) vrijedi se upoznatinajlakši način identificiranja korijena. Zove se dihotomija i odnosi se na intuitivne metode. Algoritam za pronalaženje korijena temelji se na teoremu da ako je za g (x) kontinuirano na [x0, x1] zadovoljeno je stanje različitih znakova, a zatim na razmatranom intervalu postoji najmanje 1 korijen g (x) = 0.
Da biste ga pronašli, morate podijeliti segment [x0, x1] na pola i označite sredinu kao x2... Tada su moguće dvije mogućnosti: g (x0) * g (x2) ili g (x2) * g (x1) jednake su ili manje od 0. Odaberite onu za koju je istinita jedna od ovih nejednakosti. Ponavljamo gornji postupak sve dok dužina [x0, x1] neće postati manja od određene unaprijed odabrane vrijednosti koja određuje točnost određivanja korijena jednadžbe na [x0, x1].
Prednosti metode uključuju pouzdanost ijednostavnost, a nedostatak je potreba za početnim utvrđivanjem točaka u kojima g (x) poprima različite znakove, pa se ne može koristiti za korijene s jednakom mnoštvom. Štoviše, nije uopćen na slučaj sustava jednadžbi ili kada je riječ o složenim korijenima.
Pretpostavimo da želimo riješiti jednadžbu g (x) = 2x5 + x - 1 = 0.Kako dulje vrijeme ne bismo tražili prikladan segment, gradimo graf koristeći, na primjer, dobro poznati program "Excel". Vidimo da je bolje uzeti vrijednosti iz intervala [0,1] kao segment za lokalizaciju korijena. Možemo biti sigurni da ima barem jedan korijen željene jednadžbe.
g "(x) = 10x4 + 1, to jest, to je monotono rastuća funkcija, tako da na odabranom segmentu postoji samo 1 korijen.
Zamijenite krajnje točke u jednadžbu.Imamo 0 odnosno 1. U prvom koraku uzimamo točku 0.5 kao rješenje. Tada je g (0,5) = -0,4375. To znači da će sljedeći segment koji se dijeli na pola biti [0,5, 1]. Njegova srednja točka je 0,75. Vrijednost funkcije u njemu je 0,226. Uzimamo u obzir segment [0,5, 0,75] i njegovu sredinu koja se nalazi u točki 0,625. Procijenite vrijednost g (x) od 0,625. Jednako je -0,11, što je negativno. Na temelju ovog rezultata odaberite segment [0.625, 0.75]. Dobivamo x = 0,6875. Tada je g (x) = -0,00532. Ako je točnost rješenja 0,01, tada možemo pretpostaviti da je željeni rezultat 0,6875.
Ova metoda pronalaženja korijena Newtonovom metodom tangenta popularna je zbog svoje vrlo brze konvergencije.
Temelji se na dokazanoj činjenici da ako je xn - aproksimacija korijena f (x) = 0 takva da je f "C1, tada će sljedeća aproksimacija biti u točki gdje je jednadžba tangente na f (x) nula, tj.

Zamjena x = xn + 1 i postavite y na nulu.
Tada algoritam metode tangente izgleda ovako:

Pokušajmo upotrijebiti klasičnu Newtonovu metodu tangente i pronaći rješenje neke nelinearne jednadžbe koje je analitički teško ili nemoguće pronaći.
Neka bude potrebno identificirati korijene za x3 Na primjer, + 4x - 3 = 0 s određenom preciznošću0,001. Kao što znate, grafikon bilo koje funkcije u obliku polinoma neparnog stupnja mora presijecati os OX barem jednom, odnosno nema potrebe sumnjati u postojanje korijena.
Prije rješavanja našeg primjera metodom tangente, gradimo graf f (x) = x3 + 4x - 3 točka. To je vrlo lako učiniti, na primjer, pomoću Excel proračunske tablice. Iz rezultirajućeg grafa vidjet će se da na [0,1] siječe OX os i funkciju y = x3 + 4x - 3 se monotono povećava. Možemo biti sigurni da će na [0,1] jednadžbe x3 + 4x - 3 = 0 ima rješenje i jedino je.
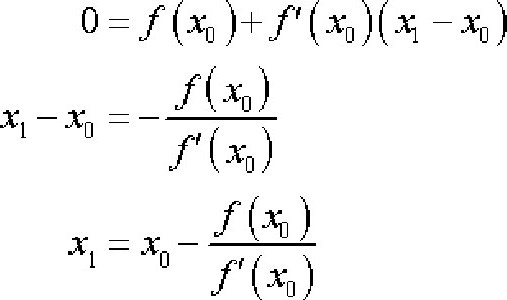
Bilo koje rješenje jednadžbi tangentnom metodom započinje izračunavanjem f "(x). Imamo:
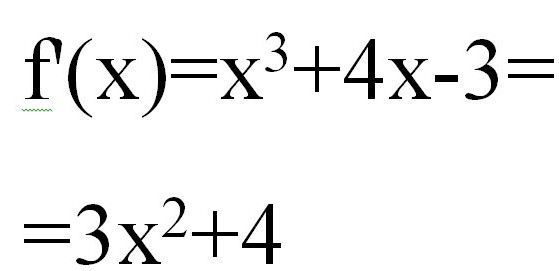
Tada će drugi izvod imati oblik x * 6.
Pomoću ovih izraza možemo napisati formulu za identificiranje korijena jednadžbe metodom tangente u obliku:

Dalje, trebate odabrati početnu aproksimaciju, tj. Da biste se bavili određivanjem koje točke uzeti u obzir početnu točku (ob.x0) za iterativni postupak. Razmotrimo krajeve segmenta [0,1]. Prikladni smo za onu za koju je uvjet funkcije i njezin drugi izvod u x0... Kao što vidite, prilikom zamjene x0 = 0 krši se, ali x0 = 1 je u redu.
Jer

onda ako nas rješenje zanima metodom tangenti s točnošću e, tada je vrijednost xn može se smatrati zadovoljavanjem zahtjeva problema, pod uvjetom da nejednakost | f (xn) / f ’(xn) | <e.
Na prvom koraku rješavanja problema tangentnom metodom imamo:

Prethodni se primjer može riješiti puno lakše i brže ako izračune ne izvodite ručno (pomoću kalkulatora), već koristite mogućnosti Microsoftovog procesora proračunskih tablica.
Da biste to učinili, u Excelu morate stvoriti novu stranicu i ispuniti njezine ćelije sljedećim formulama:
Dalje, morate "razvući" formule u stupce C, D i E, prvo za dva retka, a nakon što se vrijednosti pojave u njima, učinite isto sa stupcem B.
U određenom zadatku pojavit će se već u ćeliji B10natpis "Završetak iteracija", a za rješenje problema trebat ćete uzeti broj zapisan u ćeliji smještenoj u jednom retku iznad. Za nju možete odabrati zasebni stupac koji se može proširiti unosom tamo uvjetne formule prema kojoj će se tamo zapisati rezultat ako sadržaj u jednoj ili drugoj ćeliji stupca B poprimi oblik "Završetak iteracija".
Pokušajmo dobiti rješenje nelinearne jednadžbe y = x4 - 4 - 2 * x tangentnom metodom u Pascalu.
Koristimo pomoćnu funkciju kojapomoći će izvršiti približni izračun f "(x) = (f (x + delta) - f (x)) / delta. Kao uvjet za završetak iterativnog postupka, odabiremo ispunjenje nejednakosti | x0-x1| <neki mali broj. U Pascalu to zapisujemo kao abs (x0 - x1) <= epsilon.
Program je izvanredan po tome što ne zahtijeva ručni izračun izvedenice.

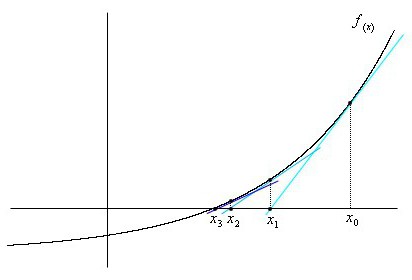
Razmotrite drugi način prepoznavanja korijenanelinearne jednadžbe. Postupak ponavljanja sastoji se u činjenici da se kao sukcesivne aproksimacije željenog korijena za f (x) = 0 uzimaju vrijednosti točaka presijecanja tetive s apscisama krajnjih točaka a i b s OX , označeno kao x1, ..., xn ... Imamo:
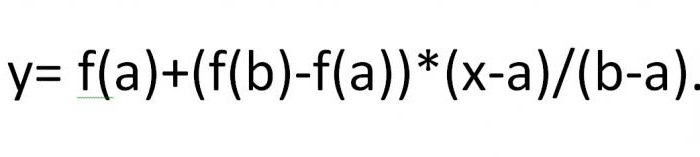
Za točku u kojoj tetiva presijeca os OX, izraz će biti zapisan kao:

Neka je drugi izvod pozitivan za x £ [a, b] (suprotan slučaj svest će se na razmatrani ako napišemo - f (x) = 0). U ovom je slučaju graf y = f (x) krivulja ispupčena na dnu i smještena ispod tetive AB... Mogu biti 2 slučaja: kada funkcija ima pozitivnu vrijednost u točki a ili je negativna u točki b.
U prvom slučaju odabiremo kraj a kao fiksni, a za x0 uzeti bod b. Tada uzastopne aproksimacije gore predstavljenom formulom tvore slijed koji se monotono smanjuje.
U drugom je slučaju krajnja točka b fiksna na x0 = a. Vrijednosti x dobivene u svakom koraku ponavljanja tvore slijed koji se monotono povećava.
Stoga možemo ustvrditi da:
Iteracije se mogu nastaviti sve dok se ne zadovolje uvjeti za blizinu korijena u ovom i prethodnom koraku ponavljanja modulo abs (xm - xm - 1) <e.
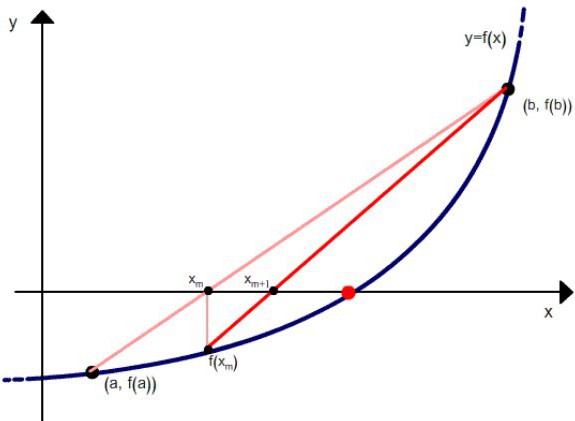
Kombinirana metoda akorda i tangenta omogućuje vam utvrđivanje korijena jednadžbe,prilazeći im s različitih strana. Takva vrijednost, pri kojoj graf f (x) prelazi OX, omogućuje pročišćavanje otopine mnogo brže nego za svaku od metoda zasebno.
Pretpostavimo da trebate pronaći korijene f (x) = 0 akooni su na [a, b]. Možete primijeniti bilo koju od gore opisanih metoda. Međutim, najbolje je isprobati kombinaciju toga dvoje, što će uvelike povećati točnost korijena.
Razmotrimo slučaj s početnom aproksimacijom koja odgovara uvjetu da prvi i drugi izvodi imaju različite znakove u određenoj točki x.
U takvim uvjetima rješavanje nelinearnih jednadžbi tangentnom metodom omogućuje pronalaženje korijena s viškom ako je x0= b, a metoda koja koristi akorde s fiksnim krajem b dovodi do pronalaska približnog korijena s nedostatkom.
Koriste se formule:

Sada se potreban traženi korijen x mora tražiti u intervalu [a1, b1]. Sljedeći je korak primjena kombinirane metode na ovaj segment. Postupajući tako, dobivamo formule oblika:

Ako se dogodi razlika u znakovima prve i druge izvedenice, tada, tvrdeći na sličan način, radi pročišćavanja korijena, dobivamo sljedeće rekurzivne formule:

Procijenjena nejednakost | bn+1 - an+1| <e. Drugim riječima, u praksi morate pronaći rješenje pomoću dvije metode, ali u svakom koraku morate saznati koliko su rezultati međusobno bliski.
Ako je gornja nejednakost istinita, tada ukao korijen nelinearne jednadžbe na danom segmentu uzimamo točku koja je točno u sredini između rješenja pronađenih u određenom koraku iteracije.
Kombinirana metoda lako se primjenjuje u okruženju TURBO PASCAL. Ako želite, možete pokušati izvršiti sve izračune tabličnom metodom u programu Excel.
U potonjem slučaju odabire se nekoliko stupaca za rješavanje problema pomoću akorda i odvojeno za metodu koju je predložio Isaac Newton.
Štoviše, svaki se redak koristi za pisanjeizračuni u određenom koraku ponavljanja pomoću dvije metode. Zatim se lijevo od područja rješenja, na aktivnoj radnoj stranici, označava stupac u koji se unosi rezultat izračunavanja modula razlike između vrijednosti sljedećeg iterativnog koraka za svaku od metoda. Drugi se može koristiti za unos rezultata izračuna prema formuli za izračunavanje logičke strukture "IF", koja se koristi za utvrđivanje je li uvjet ispunjen ili ne.
Sada znate riješiti složene jednadžbe. Tangentna metoda, kao što ste već vidjeli, prilično je jednostavno implementirati, kako u Pascalu, tako i u Excelu. Stoga uvijek možete utvrditi korijene jednadžbe koju je teško ili nemoguće riješiti pomoću formula.


























