
לאונרד אוילר (1707-1783) - מפורסם שוויצרימתמטיקאי רוסי, חבר האקדמיה למדעים של סנט פטרבורג, חי רוב חייו ברוסיה. המפורסם ביותר בניתוח מתמטי, סטטיסטיקה, מדעי המחשב והלוגיקה הוא מעגל אוילר (אוילר- Venn דיאגרמה), המשמש לציון היקף המושגים ואת קבוצות של אלמנטים.
ג'ון ון (1834-1923) - פילוסוף ולוגיקאי אנגלי, ממחברי דיאגרמת אוילר-ון.
המושג לוגיקה פירושו צורהוחושבת את המאפיינים החיוניים של מעמד של אובייקטים הומוגניים. הם מסומנים על ידי אחד או קבוצה של מילים: "מפת העולם", "אקורדים quintseptic דומיננטי", "יום שני", וכו '
במקרה שבו האלמנטים של נפח של מושג אחדבאופן מלא או חלקי, בנפח אחר, הם מדברים על מושגים תואמים. אם שום מרכיב בנפח של מושג מוגדר אינו שייך לנפח אחר, יש לנו מקום עם מושגים שאינם תואמים.

בתורו, לכל אחד מסוגי המושגים יש מערכת יחסים משלו. עבור מושגים תואמים, אלה הם:
עבור לא תואם:
באופן שיטתי, היחסים בין המושגים לוגיקה הוא מסומן בדרך כלל בעזרת מעגלים אוילר- Venn.
במקרה זה, המושגים מרמזים על אותו נושא. לפיכך, הכרכים של מושגים אלה הם לגמרי אותו דבר. לדוגמה:
א - זיגמונד פרויד;
ב 'הוא מייסד הפסיכואנליזה.

או:
A הוא הכיכר;
B הוא מלבן שווה צלעות;
C הוא מעוין שווה ערך.
מעגלי אוילר צירוף מקרים משמשים לציון.
קטגוריה זו כוללת מושגים שיש בהם אלמנטים משותפים הקשורים למעבר מוצלב. כלומר, עוצמת הקול של אחד המושגים כלולה בחלקה בנפח של האחר:
א - מורה;
חובב מוזיקה בתוך.

כפי שניתן לראות מדוגמא זו, היקף המושגיםחופפים באופן חלקי: קבוצה מסוימת של מורים עשויה להתברר כחובבת מוזיקה, ולהיפך - בקרב חובבי המוסיקה ישנם נציגים של המקצוע הפדגוגי. גישה דומה תהיה במקרה שבו, למשל, "תושב העיר" פועל כמושג, ו"נהג מכונית "פועל כ- B.
מוגדר באופן סכמטי כשונה בסולם.מעגל אוילר. היחסים בין המושגים במקרה זה מאופיינים בכך שהמושג הכפוף (קטן יותר בנפח) נכלל במלואו תחת הכפוף (גדול יותר בנפח). יתרה מזאת, התפיסה הכפופה לא ממצה את הכפופה לחלוטין.
לדוגמה:
א 'הוא עץ;
אורן.
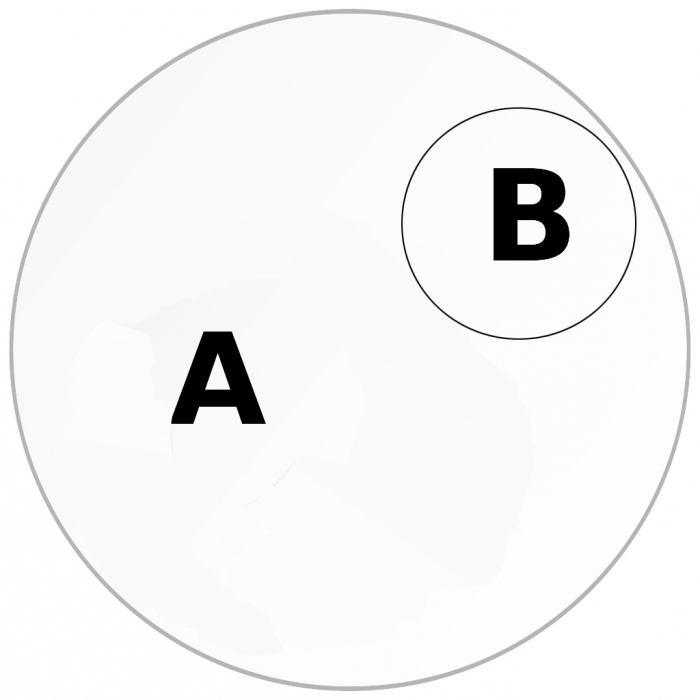
מושג B יהיה כפוף למושג A. מכיוון שאורן מתייחס לעצים, מושג A הופך בדוגמה זו להיות כפוף, "סופג" את נפח מושג B.
מערכת יחסים מאפיינת שני מושגים או יותר שהם בלעדיים הדדית, אך יחד עם זאת שייכים למעגל שבטי משותף מסוים. לדוגמא:
א - קלרינט;
בגיטרה;
C הוא הכינור;
D הוא כלי נגינה.
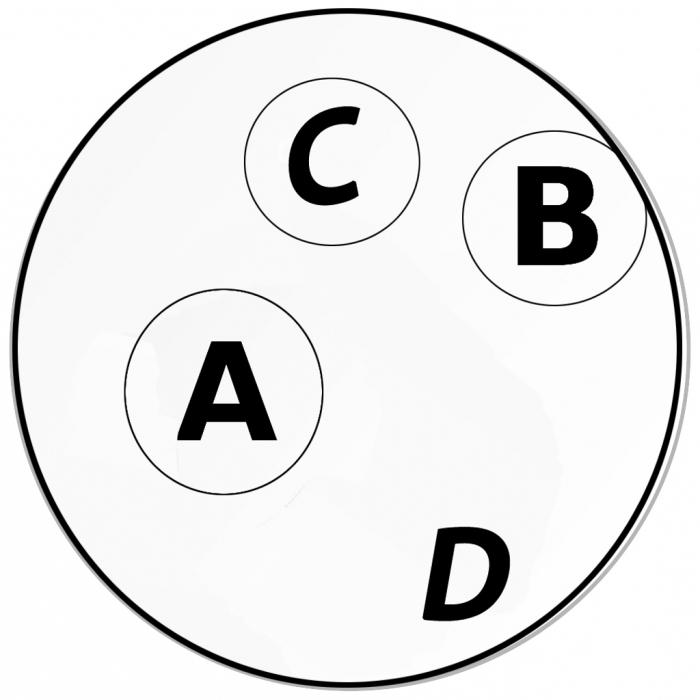
מושגים A, B, C אינם מצטלבים זה בזה, אולם כולם שייכים לקטגוריה של כלי נגינה (מושג D).
קשרים מנוגדים בין מושגיםרומז שמושגים אלה קשורים לאותו סוג. במקרה זה, לאחד המושגים יש תכונות (תכונות) מסוימות, ואילו השני מכחיש אותם, ומחליף את ההפך באופיו. לפיכך, אנו עוסקים באנטונימיות. לדוגמא:
א הוא גמד;
ב 'הוא ענק.

במערכת היחסים ההפוכה בין מושגים, מעגל אוילר מחולק לשלושה מקטעים, הראשון מהם תואם למושג A, השני למושג B והשלישי לכל שאר המושגים האפשריים.
במקרה זה, שני המושגים הםמינים מאותו הסוג. כמו בדוגמה הקודמת, אחד המושגים מציין איכויות (תכונות) מסוימות, ואילו האחר שולל אותן. עם זאת, בשונה מיחסי ההפך, המושג השני, ההפוך, אינו מחליף את התכונות המוכחשות בתכונות אלטרנטיביות אחרות. לדוגמא:
A היא משימה קשה;
B היא משימה פשוטה (שאינה A).

מביע את נפח המושגים מסוג זה, מעגל אוילרמחולק לשני חלקים - הקישור השלישי, ביניים במקרה זה לא קיים. לפיכך, מושגים הם גם אנטונים. במקביל, אחד מהם (A) הופך לחיובי (מאשר סימן), והשני (B או שאינו A) הופך לשלילי (מכחיש את הסימן המקביל): "נייר לבן" - "לא נייר לבן", "היסטוריה רוסית" - "היסטוריה זרה" וכו '.
כך, היחס בין נפחי המושגים ביחס זה לזה הוא מאפיין מפתח המגדיר מעגלי אוילר.
עליכם גם להבחין בין מושגי האלמנטים ו-מגדיר שהנפח מיוצג על ידי מעגלי אוילר. מושג הסט מושאל ממדע מתמטי ובעל משמעות רחבה למדי. דוגמאות בלוגיקה ומתמטיקה מציגות אותו כאוסף מסוים של אובייקטים. האובייקטים עצמם הם מרכיבים בקבוצה זו. "ההמון הוא הרבה שניתן לחשוב עליו כאחד" (ג'ורג 'קנטור, מייסד תורת הקבוצות).
ייעוד הסטים מהווןאותיות: A, B, C, D ... וכו ', אלמנטים של סטים - אותיות קטנות: a, b, c, d ... וכו'. דוגמאות לסטים יכולים להיות תלמידים באותה כיתה, ספרים העומדים על מדף מסוים ( או למשל, כל הספרים בספרייה מסוימת), דפים ביומן, פירות יער בשכונת יער וכו '.
בתורו, אם סט מסוים אינואינו מכיל אלמנטים, הוא נקרא ריק ומסומן על ידי השלט Ø. לדוגמה, קבוצת נקודות ההצטלבות של קווים מקבילים, קבוצת הפתרונות של המשוואה x2 = -5.
לפתור מספר רב של משימות באופן פעילמשתמשים במעגלי אוילר. דוגמאות בלוגיקה מדגימות בבירור את הקשר בין פעולות לוגיות ותורת הקבוצות. במקרה זה משתמשים בטבלאות אמת של מושגים. לדוגמה, המעגל המצוין בשם A מייצג אזור של אמת. לפיכך, האזור שמחוץ למעגל ייצג שקר. כדי לקבוע את שטח התרשים לניתוח הגיוני, צל את האזורים המגדירים את מעגל אוילר שבו הערכים שלו לאלמנטים A ו- B נכונים.
השימוש במעגלי אוילר נמצא רחביישום מעשי בתעשיות שונות. לדוגמא, במצב בחירה מקצועית. אם הנושא מודאג מהבחירה במקצוע עתידי, הוא עשוי להיות מונחה על ידי הקריטריונים הבאים:
W - מה אני אוהב לעשות?
D - מה אני מקבל?
P - איך אוכל להרוויח כסף טוב?
בואו לתאר זאת בצורה של תרשים: מעגלי אוילר (דוגמאות בלוגיקה הן הקשר הצומת):

התוצאה תהיה אותם מקצועות שמוצאים עצמם בצומת שלושת המעגלים.
חוגי אוילר-ון תופסים מקום נפרד במתמטיקה (תורת הקבוצות) בחישוב שילובים ותכונות. מעגלי אוילר של קבוצת האלמנטים סגורים בתמונת מלבן המסמל את הסט האוניברסלי (U). במקום מעגלים, ניתן להשתמש גם בדמויות סגורות אחרות, אך מהותה אינה משתנה. הנתונים מצטלבים זה בזה, על פי תנאי הבעיה (במקרה הכללי ביותר). כמו כן, יש לסמן את הנתונים הללו בהתאם. כאלמנטים מהערכות הנחשבות, נקודות הממוקמות בתוך קטעים שונים של התרשים יכולים לפעול. על בסיסו, ניתן לבקוע אזורים ספציפיים, ובכך לייעד את התפאורות החדשות.

עם קבוצות אלה מותר לבצעפעולות מתמטיות בסיסיות: תוספת (סכום קבוצות האלמנטים), חיסור (הפרש), כפל (מוצר). בנוסף, בזכות דיאגרמות אוילר-ון, ניתן לבצע פעולות של השוואת סטים לפי מספר האלמנטים הכלולים בהם, לא לספור אותם.


























