
Kosmosā plakni var iestatīt dažādiveidi (viens punkts un vektors, divi punkti un vektors, trīs punkti utt.). Paturot to prātā, plaknes vienādojumam var būt dažādas formas. Tāpat, ja ir izpildīti noteikti nosacījumi, plaknes var būt paralēlas, perpendikulāras, krustojošas utt. Mēs par to runāsim šajā rakstā. Mēs iemācīsimies sastādīt plaknes vispārējo vienādojumu un daudz ko citu.
Pieņemsim, ka ir atstarpe R3, kurai ir taisnstūra XYZ koordinātu sistēma. Definēsim vektoru α, kas tiks atbrīvots no sākuma punkta O. Caur vektora α galu uzzīmējiet plakni P, kas būs perpendikulāra tai.
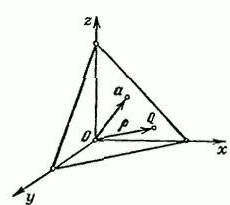
Mēs apzīmējam uz patvaļīga punkta Q = (x, y, z). Parakstīsim punkta Q rādiusa vektoru ar burtu p. Šajā gadījumā vektora α garums ir vienāds ar p = IαI un Ʋ = (cosα, cosβ, cosγ).
Šis ir vienības vektors, kas norāda uzpusē, kā arī vektors α. α, β un γ ir leņķi, kas veidojas attiecīgi starp vektoru Ʋ un telpas asu x, y, z pozitīvajiem virzieniem. Jebkura punkta QϵП projekcija uz vektoru Ʋ ir nemainīga vērtība, kas ir vienāda ar p: (p, Ʋ) = p (p≥0).
Iepriekš minētajam vienādojumam ir jēga, ja p = 0.Vienīgais, ka plakne P šajā gadījumā krustos ar punktu O (α = 0), kas ir sākumpunkts, un no punkta O izstarotais vienības vektors Ʋ būs perpendikulārs P, neskatoties uz tā virzienu, kas nozīmē, ka vektors Ʋ tiek noteikts ar precīzu zīmi. Iepriekšējais vienādojums ir mūsu plaknes P vienādojums, kas izteikts vektora formā. Bet koordinātās tā izskats būs šāds:

P šeit ir lielāks vai vienāds ar 0. Mēs esam atraduši plaknes vienādojumu telpā normālā formā.
Ja vienādojums koordinātās tiek reizināts ar jebkuru skaitli, kas nav nulle, mēs iegūstam vienādojumu, kas ir līdzvērtīgs dotajam, kas nosaka to pašu plakni. Tas izskatīsies šādi:

Šeit A, B, C ir skaitļi, kas vienlaikus nav nulle. Šo vienādojumu sauc par plaknes vispārējo vienādojumu.
Vispārējo vienādojumu var mainīt papildu apstākļu klātbūtnē. Apskatīsim dažus no tiem.
Pieņemsim, ka koeficients A ir vienāds ar 0. Tas nozīmē, ka šī plakne ir paralēla dotajai asij Ox. Šajā gadījumā vienādojuma forma mainīsies: Vy + Cz + D = 0.
Līdzīgi vienādojuma forma mainīsies šādos apstākļos:
Gadījumā, ja skaitļi A, B, C, D nav nulle, vienādojuma (0) forma var būt šāda:
x / a + y / b + z / c = 1,
kurā a = -D / A, b = -D / B, c = -D / C.
Rezultātā mēs iegūstam plaknes vienādojumu segmentos. Jāatzīmē, ka šī plakne krustos ar Oksa asi punktā ar koordinātām (a, 0,0), Oy - (0, b, 0) un Oz - (0,0, c).

Ņemot vērā vienādojumu x / a + y / b + z / c = 1, ir viegli vizuāli attēlot plaknes atrašanās vietu attiecībā pret doto koordinātu sistēmu.
Normālajam vektoram n līdz plaknei P ir koordinātas, kas ir šīs plaknes vispārējā vienādojuma koeficienti, tas ir, n (A, B, C).

Lai noteiktu normālās n koordinātas, pietiek zināt dotās plaknes vispārējo vienādojumu.
Izmantojot līnijas segmenta vienādojumu, kair forma x / a + y / b + z / c = 1, jo, izmantojot vispārējo vienādojumu, jūs varat pierakstīt jebkuras normālas vektora koordinātas noteiktā plaknē: (1 / a + 1 / b + 1 / c).
Ir vērts atzīmēt, ka parastais vektors palīdzatrisināt dažādas problēmas. Visbiežāk sastopamās problēmas ietver plakņu perpendikulitātes vai paralēlisma pierādīšanas problēmu, leņķu starp plaknēm vai leņķu starp plaknēm un līnijām atrašanas problēmu.
Nulles vektoru n, kas ir perpendikulārs noteiktai plaknei, dotajai plaknei sauc par normālu (normālu).
Pieņemsim, ka koordinātu telpā (taisnstūra koordinātu sistēma) Oxyz tiek dota:

Nepieciešams sastādīt vienādojumu plaknei, kas iet caur punktu Mₒ perpendikulāri normālajam n.
Kosmosā izvēlieties jebkuru patvaļīgu punktu unmēs to apzīmējam ar M (xy, z). Lai jebkura punkta M (x, y, z) rādiusa vektors būtu r = x * i + y * j + z * k, un punkta rādiusa vektors Mₒ (xₒ, yₒ, zₒ) - rₒ = xₒ * i + yₒ * j + zₒ * k. Punkts M piederēs dotajai plaknei, ja vektors МₒМ ir perpendikulārs vektoram n. Uzrakstīsim ortogonalitātes nosacījumu, izmantojot punktu produktu:
[MM, n] = 0.
Tā kā МₒМ = r - rₒ, plaknes vektora vienādojums izskatīsies šādi:
[r - rₒ, n] = 0.
Šim vienādojumam var būt cita forma.Šim nolūkam tiek izmantotas punktu produkta īpašības, un vienādojuma kreisā puse tiek pārveidota. [r - rₒ, n] = [r, n] - [rₒ, n]. Ja [rₒ, n] ir apzīmēts kā c, tad iegūstam šādu vienādojumu: [r, n] - c = 0 vai [r, n] = c, kas izsaka projekciju noturību uz rādiusa vektoru normālo vektoru doti punkti, kas pieder plaknei.
Tagad jūs varat iegūt mūsu plaknes vektoru vienādojuma rakstīšanas koordinātu formu [r - rₒ, n] = 0. Tā kā r - rₒ = (x - xₒ) * i + (y - yₒ) * j + (z - zₒ ) * k un n = A * i + B * j + C * k, mums ir:

Izrādās, ka mums ir plaknes vienādojums, kas iet caur punktu, kas ir perpendikulārs normālajam n:
A * (x- xₒ) + B * (y– yₒ) C * (z- zₒ) = 0.
Iestatīsim divus patvaļīgus punktus M ′ (x ′, y ′, z ′) un M ″ (x ″, y ″, z ″), kā arī vektoru a (a ′, a ″, a).
Tagad mēs varēsim izveidot dotās plaknes vienādojumu, kas iet caur esošajiem punktiem M ′ un M ″, kā arī jebkuru punktu M ar koordinātām (x, y, z), kas ir paralēlas dotajam vektoram a.
Turklāt vektoriem M′M = {x -x ′; y -y ′; zz ′} un M ″ M = {x ″ -x ′; y ″ -y ′; z ″ -z ′} jābūt līdzeniem ar vektoru a = (a ′, a ″, a ‴), kas nozīmē, ka (M′M, M ″ M, a) = 0.
Tātad mūsu plaknes vienādojums telpā izskatīsies šādi:
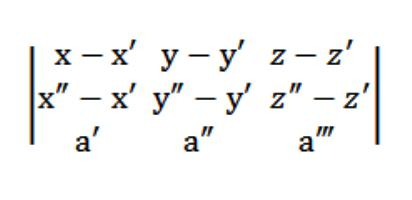
Pieņemsim, ka mums ir trīs punkti:(x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴), kas nepieder pie vienas taisnes. Nepieciešams uzrakstīt vienādojumu plaknei, kas iet caur dotajiem trim punktiem. Ģeometrijas teorija apgalvo, ka šāda veida plakne patiešām pastāv, bet tikai tā ir vienīgā un neatkārtojamā. Tā kā šī plakne krusto punktu (x ′, y ′, z ′), tā vienādojuma forma būs šāda:

Šeit A, B, C vienlaikus nav nulles. Turklāt dotā plakne krustojas vēl ar diviem punktiem: (x ″, y ″, z ″) un (x ‴, y ‴, z ‴). Šajā sakarā ir jāievēro šādi nosacījumi:

Tagad mēs varam izveidot viendabīgu vienādojumu sistēmu (lineāru) ar nezināmiem u, v, w:

Mūsu gadījumā x, y vai z ir patvaļīgspunkts, kas atbilst (1) vienādojumam. Ņemot vērā (1) vienādojumu un (2) un (3) vienādojumu sistēmu, iepriekš attēlā norādīto vienādojumu sistēmu apmierina vektors N (A, B, C), kas ir netriviāls. Tāpēc šīs sistēmas noteicējs ir vienāds ar nulli.
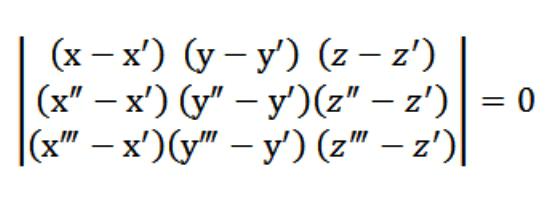
Vienādojums (1), ko mēs saņēmām, irir plaknes vienādojums. Tas iet cauri 3 punktiem, un to ir viegli pārbaudīt. Lai to izdarītu, mums ir jāpaplašina mūsu noteicējs ar elementiem, kas atrodas pirmajā rindā. No determinanta esošajām īpašībām izriet, ka mūsu plakne vienlaikus krustojas ar trim sākotnēji norādītajiem punktiem (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴) . Tas ir, mēs esam atrisinājuši mūsu priekšā izvirzīto uzdevumu.
Divstūrainais leņķis irtelpiska ģeometriska figūra, ko veido divas pusplaknes, kas izplūst no vienas taisnes. Citiem vārdiem sakot, šī ir daļa no telpas, ko ierobežo šīs pusplaknes.
Pieņemsim, ka mums ir divas plaknes ar šādiem vienādojumiem:
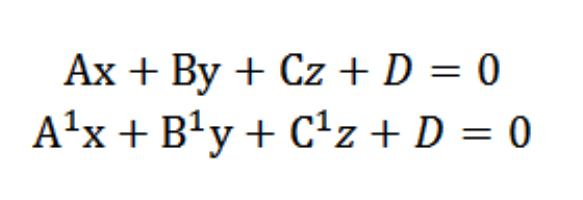
Mēs zinām, ka vektori N = (A, B, C) unN¹ = (А¹, В¹, С¹) ir perpendikulāras atbilstoši dotajām plaknēm. Šajā sakarā leņķis φ starp vektoriem N un N¹ ir vienāds ar leņķi (divstūrains), kas atrodas starp šīm plaknēm. Punktu produkts ir šāds:
NN¹ = | N || N¹ | cos φ,
tieši tāpēc
cosφ = NN¹ / | N || N¹ | = (AA¹ + BB¹ + CC¹) / ((√ (A² + B² + C²)) * (√ (A¹) ² + (B¹) ² + (C¹) ²)).
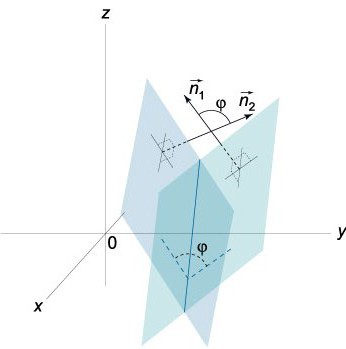
Pietiek ņemt vērā, ka 0≤φ≤π.
Faktiski divas plaknes, kas krustojas, veido divus leņķus (divstūrveida): φ1 un φ2... To summa ir vienāda ar π (φ1+ φ2= π). Kas attiecas uz kosinusu, to absolūtās vērtības ir vienādas, taču tās atšķiras pēc zīmēm, tas ir, cos φ1= -cos φ2... Ja vienādojumā (0) mēs aizstājam A, B un C attiecīgi ar skaitļiem -A, -B un -C, tad iegūtais vienādojums noteiks to pašu plakni, vienīgo leņķi φ vienādojumā cos φ = NN1/ | N || N1| tiks aizstāts ar π-φ.
Plaknes sauc perpendikulāri, starpkurš leņķis ir 90 grādi. Izmantojot iepriekš izklāstīto materiālu, mēs varam atrast plakni, kas ir perpendikulāra citam. Pieņemsim, ka mums ir divas plaknes: Ax + By + Cz + D = 0 un A¹x + B¹y + C¹z + D = 0. Mēs varam apgalvot, ka tie būs perpendikulāri, ja cosφ = 0. Tas nozīmē, ka NN¹ = AA¹ + BB¹ + CC¹ = 0.
Paralēli ir divas plaknes, kurās nav kopīgu punktu.
Nosacījums, lai plaknes būtu paralēlas (to vienādojumitas pats, kas iepriekšējā sadaļā) ir tas, ka vektori N un N¹, kas ir perpendikulāri tiem, ir kolineāri. Tas nozīmē, ka ir izpildīti šādi proporcionalitātes nosacījumi:
A / A¹ = B / B¹ = C / C¹.
Ja proporcionalitātes nosacījumi tiek pagarināti - A / A¹ = B / B¹ = C / C¹ = DD¹,
tas norāda, ka šīs lidmašīnas sakrīt. Un tas nozīmē, ka vienādojumi Ax + By + Cz + D = 0 un A¹x + B¹y + C¹z + D¹ = 0 apraksta vienu plakni.
Pieņemsim, ka mums ir plakne P, kas ir dotavienādojums (0). Ir jāatrod attālums līdz tai no punkta ar koordinātām (xₒ, yₒ, zₒ) = Qₒ. Lai to izdarītu, plaknes P vienādojums jāpārnes normālā formā:
(p, v) = p (p≥0).
Šajā gadījumā ρ (x, y, z) irmūsu punkta Q rādiusa vektors, kas atrodas uz P, p ir perpendikulāra P garums, kas tika atbrīvots no nulles punkta, v ir vienības vektors, kas atrodas virzienā a.

Atsevišķa punkta rādiusa vektora Q = (x, y, z), kas pieder pie P, kā arī dotā punkta Q rādiusa vektora starpība ρ-ρº0= (xₒ, yₒ, zₒ) ir šāds vektors, kura projekcijas absolūtā vērtība uz v ir vienāda ar attālumu d, kas jāatrod no Q0= (xₒ, yₒ, zₒ) līdz P:
D = | (ρ-ρ0, v) |, bet
(ρ-ρ0, v) = (ρ, v) - (ρ0, v) = р– (ρ0, v).
Tātad izrādās
d = | (ρ0, v) -p |.
Tagad redzams, lai aprēķinātu attālumu d no Q0 uz plakni P, ir jāizmanto plaknes vienādojuma normālā forma, vienlaikus pārejot uz p kreiso pusi un aizstājot (xₒ, yₒ, zₒ) pēdējā, nevis x, y, z.
Tādējādi mēs atradīsim iegūtās izteiksmes absolūto vērtību, tas ir, vēlamo d.
Izmantojot parametru valodu, mēs iegūstam acīmredzamo:
d = | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).
Ja dots punkts Q0 atrodas plaknes P otrā pusē, tāpat kā izcelsme, tad starp vektoru ρ-ρ0 un v ir truls leņķis, tāpēc:
d = - (ρ -ρ0, v) = (ρ0, v) -p> 0.
Gadījumā, ja punkts Q0 kopā ar koordinātu izcelsmi atrodas tajā pašā P pusē, tad izveidotais leņķis ir akūts, tas ir:
d = (ρ-ρ0, v) = р - (ρ0, v)> 0.
Rezultātā izrādās, ka pirmajā gadījumā (ρ0, v)> р, otrajā (ρ0, v) <lpp.
Pieskares plakne virsmai pieskares punktā Mº ir plakne, kurā ir visas iespējamās pieskares līknēm, kuras novilktas caur šo virsmas punktu.
Izmantojot šo virsmas vienādojuma formu F (x, y, z) = 0, pieskares plaknes vienādojums pieskares punktā Mº (xº, yº, zº) izskatīsies šādi:
Fx(xº, yº, zº) (x- xº) + Fx(xº, yº, zº) (y-yº) + Fx(xº, yº, zº) (z-zº) = 0.
Ja mēs iestatām virsmu skaidrā formā z = f (x, y), tad pieskares plakne tiks aprakstīta ar vienādojumu:
z-zº = f (xº, yº) (x- xº) + f (xº, yº) (y-yº).
Sistēma atrodas trīsdimensiju telpākoordinātas (taisnstūrveida) Oxyz, ir dotas divas plaknes P ′ un P ″, kuras krustojas un nesakrīt. Tā kā jebkuru plakni taisnstūrveida koordinātu sistēmā nosaka vispārējais vienādojums, mēs pieņemsim, ka P 'un P' ir doti ar vienādojumiem Ax + B'y + C'z + D '= 0 un A ″ x + B ″ y + C ″ z + D ″ = 0. Šajā gadījumā mums ir normālā P ′ plaknes n ′ (A ′, B ′, C ′) un P ″ plaknes normālā n ″ (A ″, B ″, C ″). Tā kā mūsu plaknes nav paralēlas un nesakrīt, šie vektori nav kolineāri. Izmantojot matemātikas valodu, mēs varam uzrakstīt šo nosacījumu šādi: n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. Ļaujiet, lai taisne, kas atrodas P ′ un P ″ krustojumā, tiks apzīmēta ar burtu a, šajā gadījumā a = P ′ ∩ P ″.
a ir taisna līnija, kas sastāv no visu punktu kopas(parastās) plaknes P ′ un P ″. Tas nozīmē, ka jebkura punkta, kas pieder taisnei a, koordinātēm vienlaikus jāatbilst vienādojumiem A'x + B'y + C'z + D '= 0 un A ″ x + B ″ y + C ″ z + D ″ = 0. Tas nozīmē, ka punkta koordinātas būs īpašs šādas vienādojumu sistēmas risinājums:

Tā rezultātā izrādās, ka risinājums (vispārīgs) no šīvienādojumu sistēma noteiks katra taisnes punkta koordinātas, kas darbosies kā P ′ un P ″ krustošanās punkts, un noteiks taisni a Oxyz koordinātu sistēmā (taisnstūrveida) telpā.


























