
Att arbeta med den mest fördelaktiga informationenlagringsmetoder är strukturer och matriser. Den senare kan innehålla vilken som helst av samma typ av data som är bekväm att använda i programmet. De används ofta vid drift av onlinebutiker och i utvecklingen av spel. Därför sorteras och byts informationen i dem upprepade gånger och logiska eller matematiska operationer utförs på dem. Ett sätt att rensa upp en matris är genom bubbelsortering. Denna publikation kommer att granska dess C-kod och permutationslogik.
Tekniska svårigheter för programmerarenbubbelsortering av en endimensionell matris representerar inte, även om den sällan används på grund av dess låga effektivitet. Det betraktas ofta på träningsstadiet som det enklaste. Men det är långt ifrån det mest effektiva. Dess algoritm består av att sekventiellt jämföra siffror och skriva om celler om villkoret är uppfyllt.

Vid den första iterationen jämförs två gradvisangränsande nummer. Om den vänstra är större, skrivs den över på platser med höger. Minus 8 och 0-villkoren uppfyller inte. Därför byter de inte platser. Noll och 5 är inte heller lämpliga. 5 och 3 är lämpliga. Vid en sådan iteration faller emellertid inte läsramen på de fem bästa, utan flyttas åt höger, eftersom 5 tidigare jämfördes med noll. Detta innebär att nästa par vänds - 3 och 9. Därefter uppmanas läsaren att titta på alla ersättningar på egen hand utan några författares kommentarer och studera bubblasorteringsalgoritmen.
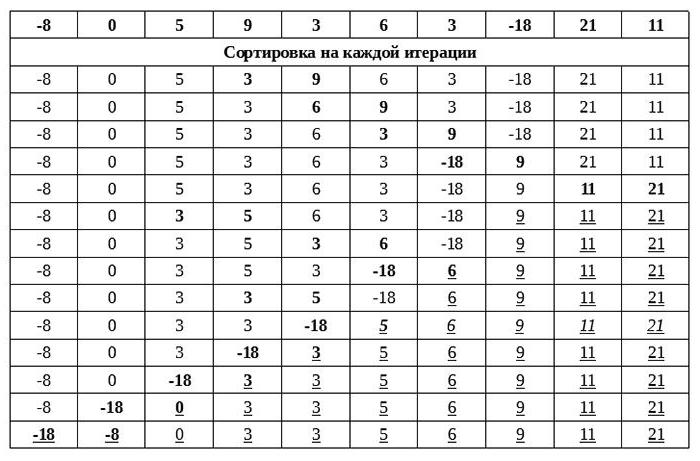
Som ett resultat av alla iterationer är matrisen gradvissorteras, och detta händer huvudsakligen så här: stora positiva siffror växlar snabbt åt höger, medan mindre och negativa siffror omorganiseras långsamt till vänster. Det ser ut som att gasbubblor i en vätska snabbt flyter upp. På grund av denna analogi kallades algoritmen bubbelsortering.
Den ideala sorteringsalgoritmen borde varaså fort som möjligt. Samtidigt bör det ta upp en liten mängd processor- och minnesresurser. Och en sådan process som bubbelsortering av en matris kan inte vara den mest energieffektiva och lönsamma. Därför hittade han inte bred tillämpning. Om det finns färre problem med minnet för tillfället, bör du oroa dig för processorresurser. Eftersom digitala matriser inte bara kan vara stora, utan stora, kommer konsumtionen av datorresurser att vara oförutsägbar.
Om bubbelsortering i princip är snabbhantera återställning av ordning i en relativt liten grupp, då i en stor kan det förekomma fel på grund av överskridande av resurser. Detta innebär att universalitetsegenskapen som ingår i algoritmen bryts mot. Dessutom har bubbelsortering N-kvadratkomplexitet och är mycket långt ifrån logaritmen för N-komplexiteten. Dessutom ökar risken för ett fel under bearbetning av en stor matris chanserna för dataförlust på grund av överskrivningsceller. Sortering efter skär eller Shell-algoritmen kommer att vara mycket mer lönsam i detta avseende.
Nedan anges i grafikapplikationendatorkod för C-språket tillåter bubbelsortering. Det återges som en separat funktion av tomtypen. Det returnerar inga värden, men med hjälp av pekare byter det elementen beroende på sorteringsförhållandena. I detta fall löser koden problemet med bubblasortering av en rad heltal i stigande ordning.
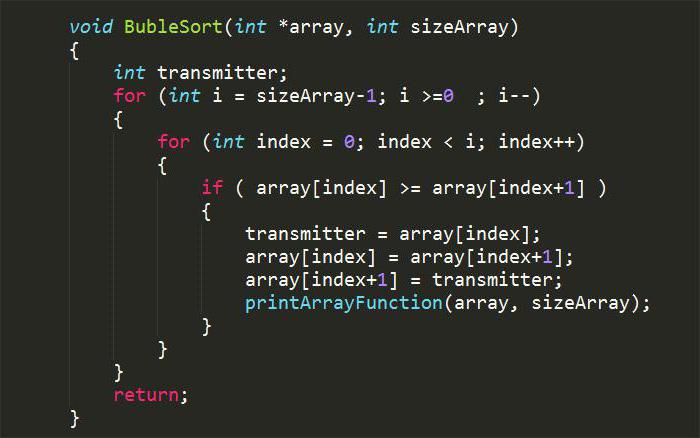
För att utföra denna funktion måste användarenskapa en matris som måste fyllas med nödvändiga värden. Detta kan göras manuellt genom att ställa in dimensionen och antalet element i början av programmet. Sedan kan du fylla matrisen med konstanta värden. Det andra alternativet är att skapa ett universellt program genom att förklara en stor endimensionell matris med 100 element.
Genom att ställa in en heltalvariabel och tilldela denvärde läst från tangentbordet kan du begränsa antalet celler som ska fyllas. Du kan också implementera funktionen för att mata in matriselement av användaren från tangentbordet med hjälp av scanf-funktionen ("% d", & värde). I det här exemplet är "% d" en modifieringssträng som säger kompilatorn att ett heltal kommer att erhållas efter skanning. Det variabla värdet kommer att lagra värdet, som är storleken på en endimensionell heltalarray.
För att använda en sorteringsalgoritm bör man göra detskicka namnet på matrisen och dess storlek till funktionen. I den situation som presenteras i en grafisk applikation kommer samtalet till sorteringsfunktionen att se ut så här: BubleSort (dataArray, sizeDataArray). Naturligtvis, i slutet av raden efter funktionen, bör du sätta ett semikolon istället för en punkt, enligt reglerna för programsyntax. Så dataArray är namnet på den matris som ska sorteras och sizeDataArray är dess storlek.

Skicka dessa parametrar till BubleSort () -funktionenkommer att leda till att istället för att använda sizeArray, som du kan se i figuren, i ett riktigt program kommer operationer att utföras med sizeDataArray. Detta innebär också att heltalet dataArray kommer att användas i BubleSort () -funktionen. Funktionerna printArrayFunction () och ArrayIntegerInputFunction () anropas på samma sätt. Den första ansvarar för utskrift, det vill säga för att visa objekt i konsolen. Och den andra behövs för att fylla den med element som användaren matat in från tangentbordet.
En sådan typ av programmering när den är isoleradoperationer utförs i form av funktioner, ökar avsevärt läsbarheten för koden och påskyndar dess utveckling. I ett sådant program tas fyllningen av matrisen från tangentbordet, dess utskrift och bubblasorteringen separat ut. Den senare kan användas för att beställa data eller som en mindre funktion för att hitta minimum och maximum för en matris.
Insättningsslag förutsätteren-för-en-jämförelse av varje element och bygga en kedja av element som redan är sorterade efter tillståndet. Som ett resultat är resultatet av varje efterföljande jämförelse att hitta en cell i vilken ett nytt värde kan placeras. Men införandet av var och en av dem utförs i den redan sorterade delen av matrisen.
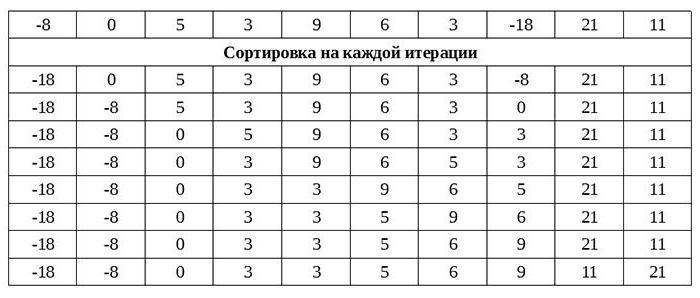
Denna bearbetning är snabbare och har mindre beräkningskomplexitet. C-koden presenteras i en grafisk applikation.

Det återges också som en funktion, i vilken inamnet på arrayen som ska beställas och storleken på arrayen skickas som argument. Här kan du se hur långsam bubblasortering är. Inserts utför liknande arbete mycket snabbare och har en kompakt programkod.


























