Insättningssortering: algoritmexempel

Det finns flera grundläggande lösningsalgoritmer.array sorteringsuppgifter. En av de mest kända bland dem är sortering efter skär. På grund av dess tydlighet och enkelhet, men låga effektivitet, används denna metod huvudsakligen i undervisning i programmering. Det låter dig förstå de grundläggande sorteringsmekanismerna.

Algoritmbeskrivning

Kärnan i införingssorteringsalgoritmen ärdet faktum att inuti källarrayen ordnas ett segment efter behov. Varje element, en i taget, jämförs med den testade delen och införs på plats. Således, efter att ha räknat upp alla elementen, ställer de sig i rätt ordning.

Beställningen av val av element kan vara vilken som helstde kan väljas godtyckligt eller enligt någon algoritm. Oftast används sekventiell uppräkning från början av matrisen, där ett ordnat segment bildas.

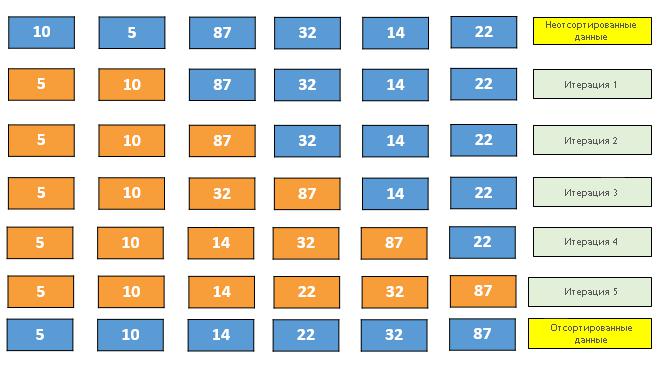
Början på sorten kan se ut så här:

1. Ta det första elementet i matrisen.
2. Eftersom det inte finns något att jämföra det med, ta själva elementet för en ordnad sekvens.
3. Gå till den andra artikeln.
4. Jämför det med det första, baserat på sorteringsregeln.
5. Byt om nödvändigt element.
6. Ta de två första elementen för en ordnad sekvens.
7. Gå till den tredje artikeln.
8. Jämför det med det andra, om nödvändigt, byt.
9. Om ersättningen görs, jämför den med den första.
10. Ta tre element för en ordnad sekvens.

Och så vidare tills slutet av den ursprungliga matrisen.

Sortera skär i verkliga livet

För tydlighetens skull är det värt att ge ett exempel på hur denna sorteringsmekanism används i vardagen.

Ta till exempel en plånbok.I sedelfacket är hundratals, femhundra och en tusendels sedlar i röran. Detta är en röra, i en sådan röra är det svårt att omedelbart hitta rätt papper. En rad anteckningar måste sorteras.

Den allra första är en sedel på 1000 rubel och omedelbart efter den - 100. Vi tar hundra och placerar den framför. Den tredje i rad - 500 rubel, den rättmätiga platsen för henne är mellan hundra och tusen.

På samma sätt sorterar vi de mottagna korten när vi spelar "Fool", så att det är lättare att navigera på dem.

Operatörer och hjälpfunktioner

Insättningssorteringsmetod accepterar ingångkällarrayen som ska beställas, jämförelsefunktionen och vid behov den funktion som definierar regeln för att räkna upp element. Oftast används den vanliga loopoperatören istället.

Det första elementet i sig är en ordnad uppsättning, så jämförelsen börjar med det andra.

En algoritm använder ofta en hjälpfunktion för att utbyta två värden (byte). Den använder en extra tillfällig variabel, som kräver minne och något saktar ner koden.

Ett alternativ är massgruppsförskjutningelement och efterföljande infogning av strömmen i det utrymme. I detta fall inträffar övergången till nästa element när jämförelsen ger ett positivt resultat, vilket indikerar rätt ordning.

Exempel på implementering

Den specifika implementeringen beror till stor del på det programmeringsspråk som används, dess syntax och strukturer.

En klassisk implementering av C-språk med en tillfällig variabel för att utbyta värden:

int i, j, temp;
för (i = 1; i  = 0; j--)
{
if (array [j] 

PHP-implementering:

funktion insertion_sort (& $ a) {
för ($ i = 1; $ i  = 0 && $ a [$ j]> $ x; $ j--) {
$ a [$ j + 1] = $ a [$ j];
}
$ a [$ j + 1] = $ x;
}
}

Här förskjuts först alla element som inte uppfyller sorteringsvillkoret åt höger, och sedan sätts det aktuella elementet in i det utrymme.

Java-kod med en stundslinga:

public static void insertionSort (int [] arr){
för (int i = 1; i  = 0 && arr [prevKey]> currElem) {
arr [prevKey + 1] = arr [prevKey];
arr [prevKey] = currElem;
prevKey--;
}
}
}

Kodens allmänna betydelse förblir oförändrad: varje element i matrisen jämförs i tur och ordning med de tidigare och byter plats med dem vid behov.

Uppskattad arbetstid

Uppenbarligen, i bästa fall, ingångenAlgoritmen kommer redan att matas in på rätt sätt. I denna situation måste algoritmen helt enkelt kontrollera varje element för att se till att den står på sin plats utan utbyte. Således beror körtiden direkt på längden på den ursprungliga matrisen O (n).

Det värsta fallet med input är en matris,sorterad i omvänd ordning. Det kommer att kräva ett stort antal permutationer, runtime-funktionen beror på antalet kvadratiska element.

Det exakta antalet permutationer för en absolut störd grupp kan beräknas med hjälp av formeln:

n * (n-1) / 2

där n är längden på den ursprungliga matrisen. Således krävs 4950 permutationer för att ordna 100 element i rätt ordning.

Insättningsmetoden är mycket effektiv för att sortera små eller delvis ordnade matriser. Det rekommenderas dock inte att användas överallt på grund av den stora komplexiteten i beräkningarna.

Algoritmen används som en hjälpare i många andra mer komplexa sorteringsmetoder.

Sortera samma värden

Införingsalgoritmen avser den så kalladehållbar sortering. Detta innebär att den inte utbyter samma element utan bevarar sin ursprungliga ordning. Stabilitetsindex är i många fall viktigt för korrekt ordning.

Ovanstående är ett bra visuellt exempel på sortering av insatser i en dans.