Чи знаєте ви, що означає "раціональний" і які числа називаються раціональними?

У далекому минулому, коли ще не була придуманасистема обчислення, люди підраховували все на пальцях. З появою арифметики і основ математики стало набагато простіше і практичніше вести облік товарів, продуктів, а також побутових предметів. Однак як виглядає сучасна система обчислення: на які види поділяються існуючі числа і що значить "раціональний вид чисел"? Давайте розберемося.

Скільки різновидів чисел існує в математиці?

Саме поняття "число" позначає якусь одиницюбудь-якого предмета, яка характеризує його кількісні, порівняльні або порядкові показники. Для того щоб правильно підрахувати кількість певних речей або провести якісь математичні операції з числами (скласти, помножити і ін.), В першу чергу слід ознайомитися з різновидами цих самих чисел.

Отже, існуючі числа можна розділити за наступними категоріями:

1. Натуральні - це ті числа, якими мипідраховуємо кількість предметів (найменше натуральне число дорівнює 1, логічно, що ряд натуральних чисел нескінченний, т. е. не існує найбільшого натурального числа). Безліч натуральних чисел прийнято позначати буквою N.
2. Цілі числа. До цього безлічі відносяться всі натуральні числа, при цьому в нього додаються і негативні значення, включаючи число "нуль". Позначення безлічі цілих чисел записують у вигляді латинської букви Z.
3. Раціональні числа - це ті, які ми подумкиможемо перетворити в дріб, чисельник якого буде належати безлічі цілих чисел, а знаменник - натуральних. Трохи нижче ми розберемо докладніше, що означає "раціональне число", і наведемо кілька прикладів.
4. Дійсні числа - безліч, в яке входять всі раціональні та ірраціональні числа. Позначається дане безліч буквою R.
5. Комплексні числа містять в собі частинудійсного і частина змінного числа. Використовуються комплексні числа в рішенні різних кубічних рівнянь, які, в свою чергу, можуть мати в формулах під знаком кореня негативне вираз (i²= -1).

Що значить "раціональний": розбираємо на прикладах

Якщо раціональними вважаються ті числа, які миможемо представити у вигляді звичайного дробу, то виходить, що всі позитивні і негативні цілі числа також входять в безліч раціональних. Адже будь-яке ціле число, наприклад 3 або 15, можна представити у вигляді дробу, де в знаменнику буде одиниця.

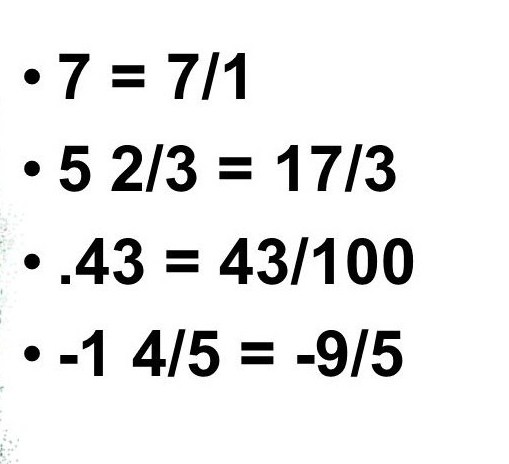
Дробу: -9/3; 7/5, 6/55 - ось приклади раціональних чисел.

Що значить "раціональне вираз"?

Йдемо далі. Ми вже розібрали, що означає раціональний вид чисел. Давайте тепер уявімо собі математичний вираз, який складається з суми, різниці, добутку або приватного різних чисел і змінних. Ось приклад: дріб, у чисельнику якого сума двох або декількох цілих чисел, а знаменник містить в собі як ціле число, так і якусь змінну. Саме такий вислів і називають раціональним. Виходячи з правила "на нуль ділити не можна" можна здогадатися, що значення даної змінної не може бути таким, щоб значення знаменника зверталося в нуль. Тому при вирішенні раціонального виразу випливає спочатку визначити область значення змінної. Наприклад, якщо в знаменнику такий вираз: x + 5-2, то виходить, що "x" не може бути дорівнює -3. Адже в такому випадку все вираз перетворюється в нуль, тому при вирішенні необхідно виключити ціле число -3 для даної змінної.

Як правильно вирішувати раціональні рівняння?

Раціональні вирази можуть містити в собідосить-таки велика кількість чисел і навіть 2 змінні, тому часом їх рішення стає скрутним. Для полегшення вирішення такого виразу рекомендується провести якісь операції раціональним шляхом. Отже, що означає "раціональним способом" і які правила необхідно застосовувати при вирішенні?

1. Перший вид, коли достатньо всього лише спроститивираз. Для цього можна вдатися до операції скорочення чисельника і знаменника до непріводімие величини. Наприклад, якщо в чисельнику є вираз 18x, а в знаменнику 9х, то, скорочуючи обидва показники на 9x, отримуємо просто ціле число, рівне 2.
2. Другий спосіб практичний тоді, коли в чисельнику маємо одночлен, а в знаменнику - многочлен. Розберемо на прикладі: в чисельнику маємо 5x, а в знаменнику - 5x + 20x². В такому випадку краще всього винести змінну взнаменнику за дужки, отримаємо такий вигляд знаменника: 5x (1 + 4x). А тепер можна скористатися першим правилом і спростити вираз, скоротивши 5x в чисельнику і в знаменнику. В результаті отримаємо дріб виду 1/1 + 4x.

Які дії можна виконувати з раціональними числами?

Безліч раціональних чисел має ряд своїхособливостей. Багато з них досить схожі з характеристикою, яка присутня у цілих і натуральних чисел, з огляду на те що останні завжди входять в безліч раціональних. Ось кілька властивостей раціональних чисел, знаючи які, можна з легкістю вирішити будь-раціональний вираз.

1. Властивість коммутативности дозволяє підсумувати два або кілька чисел, незалежно від їх черговості. Простіше кажучи, від зміни місць доданків сума не змінюється.
2. Властивість дистрибутивности дозволяє вирішувати завдання за допомогою розподільного закону.
3. І, нарешті, операції додавання і віднімання.

Навіть школярі знають, що значить "раціональнийвид чисел "і яким чином вирішувати завдання на основі таких виразів, тому дорослому освіченій людині просто необхідно згадати хоча б ази безлічі раціональних чисел.