
В одному можна бути впевненим на всі стовідсотків, що на питання, чому дорівнює квадрат гіпотенузи, будь-яка доросла людина сміливо відповість: «Сумі квадратів катетів». Ця теорема міцно засіла у свідомості кожної освіченої людини, але досить лише попросити кого-небудь її довести, і тут можуть виникнути складності. Тому давайте згадаємо і розглянемо різні способи доведення теореми Піфагора.
Теорема Піфагора знайома практично кожному, алечомусь біографія людини, який справив її на світло, не так популярна. Це можна виправити. Тому перш ніж вивчити різні способи доведення теореми Піфагора, потрібно коротко познайомитися з його особистістю.

Піфагор - філософ, математик, мислитель родом зСтародавній Греції. Сьогодні дуже складно відрізнити його біографію від легенд, які склалися в пам'ять про цю велику людину. Але як випливає з праць його послідовників, Піфагор Самоський народився на острові Самос. Його батько був звичайний каменеріз, а ось мати походила зі знатного роду.
Судячи з легендою, поява на світ Піфагорапередбачила жінка на ім'я Піфія, в чию честь і назвали хлопчика. За її передбачення народжений хлопчик повинен був принести багато користі і добра людству. Що взагалі-то він і зробив.
В юності Піфагор переїхав з острова Самос вЄгипет, щоб зустрітися там з відомими єгипетськими мудрецями. Після зустрічі з ними він був допущений до навчання, де і пізнав усі великі досягнення єгипетської філософії, математики та медицини.
Ймовірно, саме в Єгипті Піфагор надихнувсявеличністю і красою пірамід і створив свою велику теорію. Це може шокувати читачів, але сучасні історики вважають, що Піфагор не доводяться свою теорію. А лише передав своє знання послідовникам, які пізніше і завершили всі необхідні математичні обчислення.
Як би там не було, сьогодні відома не однаметодика докази даної теореми, а відразу декілька. Сьогодні залишається лише гадати, як саме древні греки виробляли свої обчислення, тому тут розглянемо різні способи доведення теореми Піфагора.
Перш ніж починати будь-які обчислення, потрібно з'ясувати, яку теорію належить довести. Теорема Піфагора звучить так: «У трикутнику, у якого один з кутів дорівнює 90про, Сума квадратів катетів дорівнює квадрату гіпотенузи ».
Всього існує 15 різних способів доведення теореми Піфагора. Це досить велика цифра, тому приділимо увагу найпопулярнішим з них.
Спочатку позначимо, що нам дано. Ці дані будуть поширюватися і на інші способи доказів теореми Піфагора, тому варто відразу запам'ятати всі наявне позначення.
Припустимо, дано прямокутний трикутник, з катетами а, в і гіпотенузою, що дорівнює с. Перший спосіб докази грунтується на тому, що з прямокутного трикутника потрібно домалювати квадрат.
Щоб це зробити, потрібно до катету довжиною адомалювати відрізок рівний катету в, і навпаки. Так повинно вийти дві рівні сторони квадрата. Залишається тільки намалювати дві паралельні прямі, і квадрат готовий.
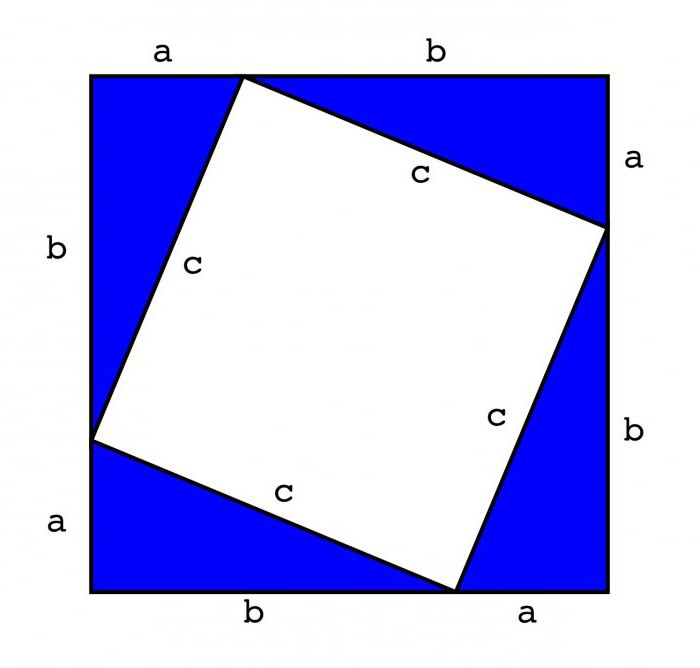
Усередині вийшла фігури потрібно накреслити щеодин квадрат зі стороною рівною гіпотенузі вихідного трикутника. Для цього від вершин ас і св потрібно намалювати два паралельних відрізка рівних с. Таким чином, вийти три сторони квадрата, одна з яких і є гіпотенуза вихідного прямокутного трикутники. Залишається лише Дочерті четвертий відрізок.
На підставі отриманого малюнка можна зробити висновок, що площа зовнішнього квадрата дорівнює (а + в)2. Якщо заглянути всередину фігури, можна побачити, що крім внутрішнього квадрата в ній є чотири прямокутних трикутника. Площа кожного дорівнює 0,5ав.
Тому площа дорівнює: 4 * 0,5ав + з2= 2АВ + з2
Звідси (а + в)2= 2АВ + з2
І, отже, з2= а2+ в2
Теорема доведена.
Дана формула доведення теореми Піфагорабула виведена на підставі затвердження з розділу геометрії про подібні трикутники. У ньому йдеться, що катет прямокутного трикутника - середнім пропорційним для його гіпотенузи і відрізка гіпотенузи, що виходить з вершини кута 90про.
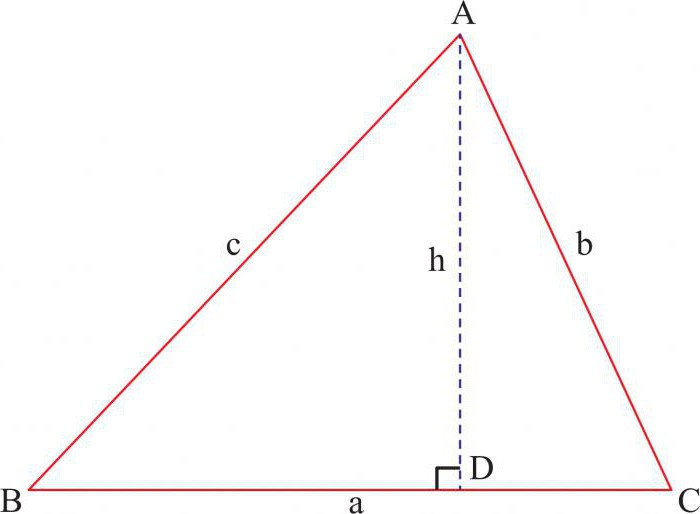
Вихідні дані залишаються ті ж, тому почнемо відразу з докази. Проведемо перпендикулярний стороні АВ відрізок СД. Грунтуючись на вищеописаному затвердження катети трикутників рівні:
АС = √АВ * АТ, СВ = √АВ * ДВ.
Щоб відповісти на питання, як довести теорему Піфагора, доказ потрібно прокласти зведенням в квадрат обох нерівностей.
АС2= АВ * АТ і СВ2= АВ * ДВ
Тепер потрібно скласти отримані нерівності.
АС2+ СВ2= АВ * (АТ * ДВ), де АТ + ДВ = АВ
Виходить що:
АС2+ СВ2= АВ * АВ
І, отже:
АС2+ СВ2= АВ2
Доказ теореми Піфагора і різні способи її вирішення потребують різнобічному підході до даної задачі. Однак цей варіант є одним з найпростіших.
Опис різних способів доведення теоремиПіфагора можуть ні про що не сказати, до тих самих пір поки самостійно не приступиш до практики. Багато методики передбачають не тільки математичні розрахунки, але і побудова з вихідного трикутника нових фігур.
В даному випадку необхідно від катета ВС добудувати ще один прямокутний трикутник ВСД. Таким чином, тепер є два трикутника із загальним катетом ВС.
Знаючи, що площі подібних фігур мають співвідношення як квадрати їх подібних лінійних розмірів, то:
Завс * з2- Sавд* в2 = Sавд* а2- SВСД* а2
Завс* (З2-в2) = А2* (Sавд-SВСД)
з2-в2= а2
з2= а2+ в2
Оскільки з різних способів доказів теореми Піфагора для 8 класу цей варіант навряд чи підійде, можна скористатися наступною методикою.
Як вважають історики, цей спосіб був впершевикористаний для доведення теореми ще в стародавній Греції. Він є найпростішим, оскільки не вимагає абсолютно ніяких розрахунків. Якщо правильно накреслити малюнок, то доказ твердження, що а2+ в2= з2 , Буде видно наочно.
Умови для даного способу буде трохи відрізнятися від попереднього. Щоб довести теорему, припустимо, що прямокутний трикутник АВС - рівнобедрений.
Гіпотенузи АС приймаємо за сторону квадрата ізакінчувати три його сторони. Крім цього необхідно провести дві діагональні прямі в отриманому квадраті. Таким чином, щоб усередині нього вийшло чотири рівнобедрених трикутника.
До катетам АВ і СВ так само потрібно Дочерті по квадрату і провести по одній діагональної прямої в кожному з них. Першу пряму креслимо з вершини А, другу - з С.

Тепер потрібно уважно вдивитися в вийшов малюнок. Оскільки на гіпотенузі АС лежить чотири трикутники, рівні вихідного, а на катетах по два, це говорить про правдивість даної теореми.
До речі, завдяки цій методиці доведення теореми Піфагора і з'явилася на світ знаменита фраза: «Піфагороі штани всі сторони рівні».
Джеймс Гарфілд - двадцятий президент Сполучених Штатів Америки. Крім того, що він залишив свій слід в історії як правитель США, він був ще й обдарованим самоучкою.
На початку своєї кар'єри він був звичайнимвикладачем в народній школі, але незабаром став директором одного з вищих навчальних закладів. Прагнення до саморозвитку і дозволило йому запропонувати нову теорію доведення теореми Піфагора. Теорема і приклад її рішення виглядає наступним чином.
Спочатку потрібно накреслити на аркуші паперу двапрямокутних трикутника таким чином, щоб катет одного з них був продовженням другого. Вершини цих трикутників потрібно з'єднати, щоб в кінцевому підсумку вийшла трапеція.
Як відомо, площа трапеції дорівнює добутку півсуми її підстав на висоту.
S = а + в / 2 * (а + в)
Якщо розглянути отриману трапецію, як фігуру, що складається з трьох трикутників, то її площа можна знайти так:
S = ав / 2 * 2 + з2/ 2
Тепер необхідно зрівняти два вихідних вираження
2АВ / 2 + с / 2 = (а + в)2/ 2
з2= а2+ в2
Про теорему Піфагора і способах її докази можна написати не один том навчального посібника. Але чи є в ньому сенс, коли ці знання не можна застосувати на практиці?
На жаль, в сучасних шкільних програмахпередбачено використання даної теореми тільки в геометричних задачах. Випускники скоро покинуть шкільні стіни, так і не дізнавшись, а як вони можуть застосувати свої знання і вміння на практиці.
Насправді ж використовувати теорему Піфагора всвоєму повсякденному житті може кожен. Причому не тільки в професійній діяльності, а й у звичайних домашніх справах. Розглянемо кілька випадків, коли теорема Піфагора і способи її докази можуть виявитися вкрай необхідними.
Здавалося б, як можуть бути пов'язані зірки і трикутники на папері. Насправді ж астрономія - це наукова сфера, в якій широко використовується теорема Піфагора.
Наприклад, розглянемо рух світлового променя в космосі. Відомо, що світло рухається в обидва боки з однаковою швидкістю. Траєкторію АВ, якій рухається промінь світла назвемо л. А половину часу, який необхідний світлу, щоб потрапити з точки А в точку Б, назвемо т. І швидкість променя - з. Виходить що: c * t = l

Якщо подивитися на цей самий промінь з іншоїплощині, наприклад, з космічного лайнера, який рухається зі швидкістю v, то при такому спостереженні тел їх швидкість зміниться. При цьому навіть нерухомі елементи стануть рухатися зі швидкістю v в зворотному напрямку.
Припустимо, комічний лайнер пливе вправо. Тоді точки А і В, між якими метається промінь, стануть рухатися вліво. Причому, коли промінь рухається від точки А в точку В, точка А встигає переміститися і, відповідно, світло вже прибуде в нову точку С. Щоб знайти половину відстані, на яке змістилася точка А, потрібно швидкість лайнера помножити на половину часу подорожі променя (t ").
d = t "* v
А щоб знайти, яку відстань за цей час зміг пройти промінь світла, потрібно позначити половину шляху нової букової s і отримати такий вираз:
s = c * t "
Якщо уявити, що точки світла С і В, а такожкосмічний лайнер - це вершини рівнобедреного трикутника, то відрізок від точки А до лайнера розділить його на два прямокутні трикутники. Тому завдяки теоремі Піфагора можна знайти відстань, яку зміг пройти промінь світла.
з2 = l2 + d2
Цей приклад, звичайно, не найвдаліший, так як тільки одиницям може пощастити випробувати його на практиці. Тому розглянемо більш приземлені варіанти застосування цієї теореми.
Сучасне життя вже неможливо уявити без існування смартфонів. Але чи багато було б від них пуття, якби вони не могли з'єднувати абонентів за допомогою мобільного зв'язку ?!
Якість мобільного зв'язку безпосередньо залежить відтого, на якій висоті перебувати антена мобільного оператора. Для того щоб обчислити, якій відстані від мобільного вишки телефон може приймати сигнал, можна застосувати теорему Піфагора.
Припустимо, потрібно знайти приблизну висоту стаціонарної вишки, щоб вона могла поширювати сигнал в радіусі 200 кілометрів.
АВ (висота вежі) = х;
ВС (радіус передачі сигналу) = 200 км;
ОС (радіус земної кулі) = 6380 км;
Звідси
ОВ = ОА + АВОВ = r + х
Застосувавши теорему Піфагора, з'ясуємо, що мінімальна висота вежі повинна скласти 2,3 кілометра.

Як не дивно, теорема Піфагора може виявитисякорисної навіть у побутових справах, таких як визначення висоти шафи-купе, наприклад. На перший погляд, немає необхідності використовувати такі складні обчислення, адже можна просто зняти мірки з допомогою рулетки. Але багато хто дивується, чому в процесі складання виникають певні проблеми, якщо все мірки були зняті більш ніж точно.
Справа в тому, що шафа-купе збирається вгоризонтальному положенні і тільки потім піднімається і встановлюється до стіни. Тому боковина шафи в процесі підйому конструкції повинна вільно проходити і по висоті, і по діагоналі приміщення.
Припустимо, є шафа-купе глибиною 800 мм. Відстань від підлоги до стелі - 2600 мм. Досвідчений мебляр скаже, що висота шафи повинна бути на 126 мм менше, ніж висота приміщення. Але чому саме на 126 мм? Розглянемо на прикладі.
За ідеальних габаритах шафи перевіримо дію теореми Піфагора:
АС = √АВ2+ √ВС2
АС = √24742+8002= 2600 мм - все сходиться.
Припустимо, висота шафи одно не 2474 мм, а 2505 мм. тоді:
АС = √25052+ √8002= 2629 мм.
Отже, ця шафа не підійде для установки в даному приміщенні. Так як при піднятті його у вертикальне положення можна завдати шкоди його корпусу.

Мабуть, розглянувши різні способи доказитеореми Піфагора різними вченими, можна зробити висновок, що вона більш ніж правдива. Тепер можна використовувати отриману інформацію в своєму повсякденному житті і бути повністю впевненим, що всі розрахунки будуть не тільки корисні, але і вірні.


























