Как да намерите минималните и максималните точки на дадена функция: характеристики, методи и примери

Функцията и изучаването на нейните характеристики отнемаедна от ключовите глави в съвременната математика. Основният компонент на всяка функция са графики, които представят не само нейните свойства, но и параметрите на производната на тази функция. Нека разгледаме тази трудна тема. И така, как най-добре да намерите максималните и минималните точки на функцията?

Функция: Определение

Всяка променлива, която по някакъв начин зависи от стойностите на друго количество, може да се нарече функция. Например, функцията f (x²) е квадратичен и определя стойностите за целия комплект x. Да приемем, че x = 9, тогава стойността на нашата функция ще бъде 9²= 81.

Функциите могат да бъдат от всякакъв вид:логически, векторно, логаритмично, тригонометрично, числено и др. Те изучавали такива изключителни умове като Lacroix, Lagrange, Leibniz и Bernoulli. Техните творби служат като крепост в съвременните начини на изучаване на функциите. Преди да откриете минималните точки, е много важно да разберете самия смисъл на функцията и нейното производно.

Производството и неговата роля

Всички функции зависят от тяхпроменливи, което означава, че те могат да променят стойността си по всяко време. На графиката тя ще бъде представена като крива, която след това се изпуска, после се издига по ордината (това е целият набор от числа "y" по вертикала на графиката). Така че определянето на точката на максимума и минимума на функцията е свързано само с тези "колебания". Ще обясним какво е това взаимоотношение.

Производството на всяка функция е графично изобразено на графикатас цел да се изследват основните му характеристики и да се изчисли колко бързо се променя функцията (т.е. тя променя стойността си в зависимост от променливата "х"). Във време, когато функцията се увеличава, графиката на нейното производно също ще се увеличи, но във всяка секунда функцията може да започне да намалява и след това производствената графика ще намалее. Точките, на които дериватът преминава от знака минус към знака плюс, се наричат ​​минималните точки. За да знаете как да намерите минималните точки, трябва по-добре да разберете концепцията за деривата.

Как да изчислим деривата?

Определяне и изчисляване на производното на функцияпредполага няколко концепции от диференциалното смятане. По принцип самата дефиниция на производното може да бъде изразена както следва: това е стойността, която показва скоростта на промяна на функцията.

Математически начин да го определим за мнозинастудентите изглеждат сложни, но всъщност всичко е много по-лесно. Необходимо е само да се следва стандартния план за намиране на деривати на всяка функция. По-долу описваме как можете да намерите минималната точка на функция, без да прилагате правила за диференциация и без да изучавате производната таблица.

1. Производството на функция може да се изчисли, като се използваграфика. За да направите това, трябва да представите самата функция, след това да вземете една точка върху нея (точка А на фиг.) Вертикално надолу начертайте линия към оста на абсцисата (точката x₀), а в точката А се допира до графикатафункция. При абсцисата и допирателната ос се образува ъгъл а. За да се изчисли стойността на бързото нарастване на функцията, е необходимо да се изчисли допирателната към този ъгъл a.
2. Оказва се, че допирателната на ъгъла между допирателната иПосоката на оста x е производната на функцията на малка секция с точка А. Този метод се счита за геометричен начин за определяне на производното.

Методи за изследване на функцията

В училищната математическа програма е възможнонамирането на минималната точка на функция по два начина. Първият метод с помощта на графиката, който вече сме разглобявали, но как определяме числената стойност на деривата? За да направите това, трябва да научите няколко формули, които описват свойствата на деривата и да помогнете да конвертирате променливите тип "x" в числа. Следният метод е универсален, така че може да се приложи към почти всички видове функции (както геометрични, така и логаритмични).

1. Необходимо е да се равнява на функция на производното на функцията, и след това се опрости експресия, като се използват правилата на диференциация.
2. В някои случаи, когато е дадена функция, впроменливата "x" стои в делителя, е необходимо да се определи обхватът на допустимите стойности, като се изключи точката "0" от нея (поради простата причина, че математиката в никакъв случай не може да бъде разделена на нула).
3. След това първоначалната форма на функцията трябва да се трансформира в просто уравнение, което прави целия израз равен на нула. Например, ако функцията изглежда така: f (x) = 2x³+ 38x, тогава, съгласно правилата на диференциацията, неговата производна е f "(x) = 3x²1. След това преобразуваме този израз в уравнението със следната форма: 3x²+1 = 0
4. След решаване на уравнението и намиране на точките "x",необходимо е те да бъдат начертани по оста х и да се определи дали производната в тези области между маркираните точки е положителна или отрицателна. След обозначението ще стане ясно в кой момент функцията започва да намалява, т.е. променя знака от минус на обратен. По този начин можете да намерите както минималните, така и максималните точки.

Правила за диференциация

Най-основният компонент при изучаването на функцията инеговото производно е познаването на правилата на диференциацията. Само с тяхна помощ можете да преобразувате обемисти изрази и големи сложни функции. Нека да ги разгледаме, има много, но всички те са много прости, благодарение на редовните свойства на силата и логаритмичните функции.

1. Производната на всяка константа е нула (f (x) = 0). Това означава, че производната f (x) = x⁵+ x - 160 ще изглежда така: f "(x) = 5x⁴1.
2. Производната на сумата от две термини: (f + w) "= f" w + fw ".
3. Производната на логаритмичната функция: (log_иd) "= d / ln a * d. Тази формула се прилага за всички видове логаритми.
4. Степен на производни: (x^п) "= n * x^N-1, Например (9x²) = 9 * 2x = 18x.
5. Производно на синусоидална функция: (sin a) "= cos a. Ако грехът на ъгъл а е 0,5, тогава неговата производна е /3 / 2.

Екстремни точки

Вече разбрахме как да намерим минималните точкивъпреки това има концепция и точка на максимална функция. Ако минимумът посочва тези точки, при които функцията преминава от знак минус на плюс, тогава максималните точки са онези точки по оста х, при които производното на функцията се променя от плюс към обратното - минус.

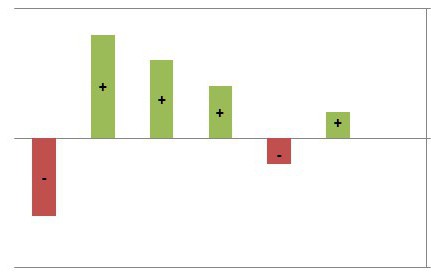
Можете да намерите максималните точки по описания по-горе метод, но трябва да имате предвид, че те посочват онези области, в които функцията започва да намалява, т.е. дериватът ще бъде по-малък от нула.

В математиката е обичайно да се обобщават и двете понятия,да ги замени с фразата "точки на екстремуми". Когато се зададе задачата за определяне на тези точки, това означава, че е необходимо да се изчисли производната на тази функция и да се намерят минималните и максималните точки.