
Jedna z nejdůležitějších věd, jejíž uplatnění může býtVidět v takových oborech, jako je chemie, fyzika a dokonce i biologie, je matematika. Studium této vědy nám umožňuje rozvíjet některé mentální vlastnosti, zlepšit abstraktní myšlení a schopnost soustředit se. Jedním z témat, která si zaslouží zvláštní pozornost v kurzu "Matematika" je doplnění a odečítání zlomků. Mnoho studentů studuje, že je obtížné. Možná náš článek pomůže lépe pochopit toto téma.
Frakce jsou stejná čísla, se kterými můžetek provádění různých akcí. Jejich rozdíl od celých čísel je v přítomnosti jmenovatele. To je důvod, proč při provádění operací se zlomky je třeba prozkoumat některé z funkcí a pravidel. Nejjednodušší případ je odečtení frakcí, jejichž jmenovatele jsou reprezentovány jako se stejným číslem. Proveďte tuto akci nebude těžké, pokud znáte jednoduché pravidlo:
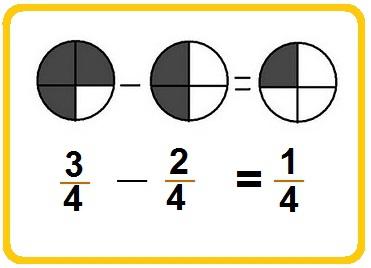
Zvažte, jak to vypadá takto:
7/19 - 3/19 = (7 - 3) / 19 = 4/19.
Z číselníku klesající frakce "7" odečtemečitatel odpočitatelného "3", dostaneme "4". Napsali jsme toto číslo v čitateli odpovědi a vložili jsme stejné číslo do jmenovatele, který byl v jmenovatelích první a druhé frakce - "19".
Na následujícím obrázku je několik podobných příkladů.

Podívejme se na komplikovanější příklad, kdy odčítáme zlomky se stejnými jmenovateli:
29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7) / 47 = n / 47.
Z čitatele redukované frakce "29"čitatele fronty všechny následující frakce - "3", "8", "2", "7". Výsledkem je výsledek "9", který píšeme v čitateli odpovědi, a v jmenovateli zapisujeme číslo, které je v jmenovateli všech těchto zlomků, "47".
Přidání a odečítání obyčejných frakcí se provádí podle stejného principu.
Zvažte, jak to vypadá takto:
1/4 + 2/4 = 3/4.
K čitateli prvního termínu frakce "1"přidejte čitatel druhého výrazu zlomku - "2". Výsledkem je "3" - zapisujeme sumu čitateli a jmenovatel opustí stejný, který byl přítomen ve zlomcích - "4".

Akce s frakcemi, které mají stejnéjmenovatele jsme již uvažovali. Jak vidíte, když znáte jednoduchá pravidla, je snadné vyřešit takové příklady. Ale co když potřebujete provést akci s frakcemi, které mají různé jmenovatele? Mnoho studentů středních škol čelí těmto příkladům. Ale tady, pokud znáte princip řešení, příklady pro vás nebudou obtížné. Existuje také pravidlo, bez něhož je řešení takových zlomků prostě nemožné.
K odečtení zlomků s různými jmenovateli je nutno snížit na stejný nejnižší jmenovatel.

Budeme mluvit více o tom, jak to udělat.
Aby několik zlomků vedlo kstejný jmenovatel musíme použít hlavní vlastnost frakce v řešení: po rozdělení nebo vynásobení čitatele a jmenovatele stejným číslem se získá frakce rovnající se tomuto.
Například zlomek 2/3 může mít takovéjmenovatele jako „6“, „9“, „12“ a t d.., to znamená, že může mít formu libovolného počtu, který je násobkem „3“. Po vynásobení čísla a jmenovatele násobením "2" se získá zlomek 4/6. Po čitatele a jmenovatele zlomku násobíme zdroj na „3“, dostaneme 6/9, a v případě, že podobný účinek na produkci s číslem „4“, dostaneme 8/12. Jedna rovnice může být takto:
2/3 = 4/6 = 6 / i = 8/12 ...
Zvažme, jak přinést několik zlomkůstejnému jmenovateli. Například vezměte zlomky na obrázku níže. Za prvé, je nutné určit, které číslo se může stát jmenovatelem pro všechny z nich. Pro zjednodušení rozložíme stávající jmenovatele na multiplikátory.
Označení frakce 1/2 a frakce 2/3nelze rozložit. Denominátor 7/9 má dva faktory 7/9 = 7 / (3 x 3), jmenovatel frakce je 5/6 = 5 / (2 x 3). Nyní je nutné určit, které faktory budou pro všechny tyto čtyři zlomky nejmenší. Vzhledem k tomu, že v prvním zlomku je v jmenovateli číslo "2", znamená to, že musí být přítomen ve všech jmenovatelích, ve zlomku 7/9 jsou dvě triplety, proto musí být oba přítomny v jmenovateli. Vzhledem k výše uvedenému určujeme, že jmenovatel se skládá ze tří faktorů: 3, 2, 3 a je rovno 3 x 2 x 3 = 18.
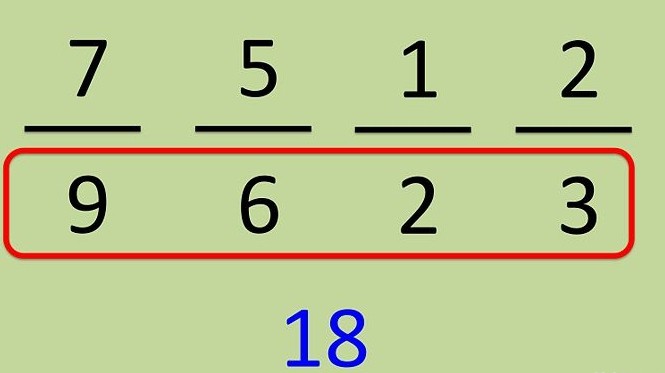
Zvažte první zlomek - 1/2.V jejím jmenovateli je "2", ale neexistuje ani jedna číslice "3", ale musí existovat dvě. Pro toto vynásobíme jmenovatele dvěma trojnásobky, ale podle vlastností zlomku musíme čitatele vynásobit dvěma trojnásobky:
1/2 = (1 x 3 x 3) / (2 x 3 x 3) = 9/18.
Podobně provádíme akce se zbývajícími částmi.
Všichni dohromady to vypadá takto:

Jak již bylo uvedeno výše, za účelemprovést sčítání nebo odčítání zlomků s různými jmenovateli, by měly vést ke společnému jmenovateli, a pak využít pravidel odčítání zlomků se stejným jmenovatelem, který již bylo řečeno.
Zvažte to například u příkladu: 4/18 - 3/15.
Najdeme násobek čísel 18 a 15:
Po nalezení jmenovatele,je třeba vypočítat faktor, který bude pro každou frakci odlišný, tj. číslo, kterým bude nutné vynásobit nejen jmenovatele, ale i čitatele. Pro toto číslo, které jsme našli (společný násobek), rozdělíme podle jmenovatele této frakce, která musí určit další faktory.
Další fází našeho rozhodnutí je snížení každé frakce na jmenovatele "90".
Jak se to dělá, už jsme řekli. Zvažte, jak je to napsáno v příkladu:
(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.
Pokud jsou zlomky s malými čísly, pak můžete určit společný jmenovatel, jako v příkladu uvedeném na obrázku níže.

Podobně se provede přidání frakcí s různými jmenovateli.
Odčítací zlomky a jejich přídavek jsme již podrobně rozebrali. Ale jak vytvořit odčítání, pokud má zlomek celou část? Opět použijte několik pravidel:

Есть и иной способ, при помощи которого можно provádět sčítání a odčítání frakcí s celými částmi. Za tímto účelem se provádějí samostatné akce s celými částmi a oddělují se akce s frakcemi a výsledky se zaznamenávají společně.

Приведенный пример состоит из дробей, которые mají stejný jmenovatel. V případě, že se jmenovatelé liší, musí být přivedeni ke stejnému a poté provést akce, jak je uvedeno v příkladu.
Další paleta frakcíje případ, kdy zlomek musí být odečten od přirozeného čísla. Na první pohled se takový příklad jeví jako obtížný vyřešit. Zde je však všechno jednoduché. K jeho vyřešení je nutné převést celé číslo na zlomek as takovým jmenovatelem, který je k dispozici v odečitatelné části. Dále provedeme odčítání podobné odčítání se stejnými jmenovateli. Například to vypadá takto:
7 - 4/9 = (7 x 9) / 9 - 4/9 = 53/9 - 4/9 = 49/9.
Odčítání frakcí uvedených v tomto článku (6třída) je základem pro řešení složitějších příkladů, které jsou zvažovány v následujících třídách. Znalost tohoto tématu se následně používá k řešení funkcí, derivátů atd. Proto je velmi důležité porozumět a porozumět činnostem se zlomky diskutovanými výše.


























