
Ένα τραπεζοειδές είναι μια ειδική περίπτωση τετραγώνου, yτο οποίο ένα ζεύγος πλευρών είναι παράλληλο. Ο όρος "trapezium" προέρχεται από την ελληνική λέξη τράπεζα, που σημαίνει "τραπέζι", "τραπέζι". Σε αυτό το άρθρο, θα εξετάσουμε τους τύπους τραπεζοειδών και τις ιδιότητές του. Επιπλέον, θα καταλάβουμε πώς να υπολογίσουμε τα μεμονωμένα στοιχεία αυτού του γεωμετρικού σχήματος. Για παράδειγμα, η διαγώνιος ενός ισοσκελούς τραπεζοειδούς, η κεντρική γραμμή, η περιοχή κ.λπ.
Αρχικά, ας καταλάβουμε τι είναιτετράπλευρο. Αυτό το σχήμα είναι μια ειδική περίπτωση πολυγώνου με τέσσερις πλευρές και τέσσερις κορυφές. Δύο κορυφές ενός τετράπλευρου που δεν είναι δίπλα ονομάζονται απέναντι. Το ίδιο μπορεί να ειπωθεί για δύο μη γειτονικές πλευρές. Οι κύριοι τύποι τετραγώνων είναι παραλληλόγραμμο, ορθογώνιο, ρόμβος, τετράγωνο, τραπεζοειδές και δελτοειδές.

Λοιπόν, πίσω στα τραπεζοειδή.Όπως είπαμε, αυτό το σχήμα έχει δύο πλευρές παράλληλες. Ονομάζονται βάσεις. Τα άλλα δύο (μη παράλληλα) είναι οι πλευρές. Στα υλικά των εξετάσεων και των διαφόρων τεστ, μπορείτε πολύ συχνά να βρείτε εργασίες που σχετίζονται με τραπεζοειδή, η λύση των οποίων απαιτεί συχνά από τον μαθητή να έχει γνώσεις που δεν προβλέπονται από το πρόγραμμα. Το σχολικό μάθημα γεωμετρίας εισάγει τους μαθητές στις ιδιότητες των γωνιών και των διαγωνίων, καθώς και στη μεσαία γραμμή ενός ισοσκελούς τραπεζοειδούς. Εκτός όμως από αυτό, το αναφερόμενο γεωμετρικό σχήμα έχει και άλλα χαρακτηριστικά. Αλλά για αυτούς λίγο αργότερα ...
Υπάρχουν πολλοί τύποι αυτής της φιγούρας. Ωστόσο, τις περισσότερες φορές συνηθίζεται να εξετάζονται δύο από αυτά - ισοσκελή και ορθογώνια.
1. Ένα ορθογώνιο τραπεζοειδές είναι ένα σχήμα στο οποίο μία από τις πλευρικές πλευρές είναι κάθετη στις βάσεις. Οι δύο γωνίες του είναι πάντα ίσες με ενενήντα μοίρες.
2. Ένα ισοσκελές τραπεζοειδές είναι ένα γεωμετρικό σχήμα με ίσες πλευρές. Αυτό σημαίνει ότι οι γωνίες στις βάσεις είναι επίσης ζεύγη ίσες.

Η κύρια αρχή είναι η χρήση τουτη λεγόμενη προσέγγιση εργασιών. Στην πραγματικότητα, δεν χρειάζεται να εισαχθούν νέες ιδιότητες αυτού του σχήματος στη θεωρητική πορεία της γεωμετρίας. Μπορούν να ανοίξουν και να διατυπωθούν στη διαδικασία επίλυσης διαφόρων προβλημάτων (καλύτερα από αυτά του συστήματος). Ταυτόχρονα, είναι πολύ σημαντικό ο δάσκαλος να γνωρίζει ποιες εργασίες πρέπει να δοθούν στους μαθητές του σχολείου σε ένα σημείο ή άλλο στην εκπαιδευτική διαδικασία. Επιπλέον, κάθε ιδιότητα τραπεζοειδούς μπορεί να αναπαρασταθεί ως βασική εργασία στο σύστημα εργασιών.
Η δεύτερη αρχή είναι η λεγόμενησπειροειδής οργάνωση της μελέτης των «αξιοσημείωτων» ιδιοτήτων του τραπεζοειδούς. Αυτό συνεπάγεται επιστροφή της μαθησιακής διαδικασίας στα επιμέρους χαρακτηριστικά ενός δεδομένου γεωμετρικού σχήματος. Αυτό διευκολύνει τους μαθητές να τις απομνημονεύσουν. Για παράδειγμα, η ιδιότητα τεσσάρων σημείων. Μπορεί να αποδειχθεί τόσο με τη μελέτη της ομοιότητας όσο και στη συνέχεια με τη χρήση διανυσμάτων. Και το ίδιο μέγεθος των τριγώνων δίπλα στις πλευρικές πλευρές του σχήματος μπορεί να αποδειχθεί εφαρμόζοντας όχι μόνο τις ιδιότητες των τριγώνων με ίσα ύψη που τραβιούνται στις πλευρές που βρίσκονται σε μία ευθεία, αλλά και χρησιμοποιώντας τον τύπο S = 1/2 (ab * sinα). Επιπλέον, μπορείτε να επεξεργαστείτε το θεώρημα των ημιτόνων σε εγγεγραμμένο τραπεζοειδές ή ορθογώνιο τρίγωνο σε περιγραφόμενο τραπεζοειδές κ.λπ.
Εφαρμογή χαρακτηριστικών "εκτός προγράμματος"ένα γεωμετρικό σχήμα στο περιεχόμενο ενός σχολικού μαθήματος είναι μια τεχνολογία εργασιών για τη διδασκαλία τους. Η συνεχής έκκληση για τις ιδιότητες που μελετήθηκαν όταν περνούν άλλα θέματα επιτρέπει στους μαθητές να αποκτήσουν βαθύτερη κατανόηση του τραπεζοειδούς και εξασφαλίζει την επιτυχία επίλυσης των ανατεθειμένων εργασιών. Λοιπόν, ας ασχοληθούμε με τη μελέτη αυτής της υπέροχης φιγούρας.

Όπως έχουμε ήδη σημειώσει, αυτό το γεωμετρικόοι φιγούρες στις πλευρές είναι ίσες. Είναι επίσης γνωστό ως κανονικό τραπεζοειδές. Και γιατί είναι τόσο αξιόλογο και γιατί πήρε τέτοιο όνομα; Οι ιδιαιτερότητες αυτού του σχήματος περιλαμβάνουν το γεγονός ότι έχει ίσες όχι μόνο τις πλευρές και τις γωνίες στις βάσεις, αλλά και τις διαγώνιες. Επιπλέον, το άθροισμα των γωνιών ενός ισοσκελούς τραπεζοειδούς είναι 360 μοίρες. Αλλά δεν είναι μόνο αυτό! Από όλα τα γνωστά τραπεζοειδή, μόνο γύρω από ένα ισοσκελές μπορεί κανείς να περιγράψει έναν κύκλο. Αυτό οφείλεται στο γεγονός ότι το άθροισμα των αντίθετων γωνιών αυτού του σχήματος είναι 180 μοίρες και μόνο κάτω από αυτήν την κατάσταση μπορεί να περιγραφεί ένας κύκλος γύρω από ένα τετράγωνο. Η επόμενη ιδιότητα του θεωρούμενου γεωμετρικού σχήματος είναι ότι η απόσταση από την κορυφή της βάσης έως την προβολή της αντίθετης κορυφής στην ευθεία που περιέχει αυτή τη βάση θα είναι ίση με την κεντρική γραμμή.
Τώρα ας καταλάβουμε πώς να βρούμε τις γωνίες ενός ισοσκελούς τραπεζοειδούς. Εξετάστε μια λύση σε αυτό το πρόβλημα, υπό την προϋπόθεση ότι είναι γνωστές οι διαστάσεις των πλευρών του σχήματος.
Συνήθως το τετράπλευρο συμβολίζεται συνήθωςγράμματα A, B, C, D, όπου BS και AD είναι οι βάσεις. Σε ένα ισοσκελές τραπεζοειδές, οι πλευρές είναι ίσες. Θα υποθέσουμε ότι το μέγεθός τους είναι ίσο με το Χ και τα μεγέθη των βάσεων είναι ίσα με τα Υ και Ζ (μικρότερα και μεγαλύτερα, αντίστοιχα). Για να εκτελέσετε τον υπολογισμό, είναι απαραίτητο να σχεδιάσετε το ύψος Ν. Από τη γωνία Β. Το αποτέλεσμα είναι ένα ορθογώνιο τρίγωνο ABN, όπου το AB είναι η υποτείνουσα και τα BN και AH είναι τα πόδια. Υπολογίζουμε το μέγεθος του ποδιού AH: αφαιρούμε το μικρότερο από τη μεγαλύτερη βάση και διαιρούμε το αποτέλεσμα με 2. Το γράφουμε με τη μορφή του τύπου: (ZY) / 2 = F. Τώρα, για να υπολογίσουμε την οξεία γωνία του τριγώνου, χρησιμοποιούμε τη συνάρτηση cos. Παίρνουμε την ακόλουθη εγγραφή: cos (β) = X / F. Τώρα υπολογίζουμε τη γωνία: β = arcos (X / F). Επιπλέον, γνωρίζοντας τη μία γωνία, μπορούμε να καθορίσουμε τη δεύτερη, γι 'αυτό εκτελούμε μια στοιχειώδη αριθμητική πράξη: 180 - β. Όλες οι γωνίες είναι καθορισμένες.
Υπάρχει επίσης μια δεύτερη λύση σε αυτό το πρόβλημα.Στην αρχή, χαμηλώνουμε το ύψος του Ν. Από τη γωνία. Υπολογίστε την τιμή του ποδιού ΒΝ. Γνωρίζουμε ότι το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου είναι ίσο με το άθροισμα των τετραγώνων των ποδιών. Παίρνουμε: BN = (X2-F2). Στη συνέχεια, χρησιμοποιούμε την τριγωνομετρική συνάρτηση tg. Ως αποτέλεσμα, έχουμε: β = αρκτάνη (BN / F). Βρέθηκε μια αιχμηρή γωνία. Στη συνέχεια, ορίζουμε μια αμβλεία γωνία με τον ίδιο τρόπο όπως στην πρώτη μέθοδο.
Αρχικά, ας γράψουμε τέσσερις κανόνες. Εάν οι διαγώνιες σε ένα ισοσκελές τραπεζοειδές είναι κάθετες, τότε:
- το ύψος του σχήματος θα είναι ίσο με το άθροισμα των βάσεων, διαιρούμενο με δύο.
- το ύψος και η μεσαία γραμμή είναι ίσα ·
- η περιοχή του τραπεζοειδούς θα είναι ίση με το τετράγωνο του ύψους (μεσαία γραμμή, το μισό άθροισμα των βάσεων) ·
- το τετράγωνο της διαγώνιας είναι ίσο με το μισό τετράγωνο του αθροίσματος των βάσεων ή δύο φορές το τετράγωνο της μεσαίας γραμμής (ύψος).
Τώρα εξετάστε τους τύπους που καθορίζουν τη διαγώνιο ενός ισοσκελούς τραπεζοειδούς. Αυτό το σύνολο πληροφοριών μπορεί να χωριστεί σε τέσσερα μέρη:
1. Τύπος του μήκους μιας διαγώνιας ως προς τις πλευρές της.
Υποθέτουμε ότι το Α είναι η κάτω βάση, το Β είναι η κορυφή, το Γ είναι ίσες πλευρές, το Δ είναι η διαγώνιος. Σε αυτή την περίπτωση, το μήκος μπορεί να καθοριστεί ως εξής:
D = √ (C2 + A * B).
2. Τύποι για το μήκος της διαγώνιας από το θεώρημα συνημίτονο.
Δεχόμαστε ότι το Α είναι η κάτω βάση, το Β είναι η πάνω,C - ίσες πλευρές, D - διαγώνιος, α (στην κάτω βάση) και β (στην άνω βάση) - τραπεζοειδείς γωνίες. Παίρνουμε τους ακόλουθους τύπους που μπορούν να χρησιμοποιηθούν για τον υπολογισμό του μήκους της διαγώνιας:
- D = √ (A2 + C2-2A * C * cosα);
- D = √ (A2 + C2-2A * C * cosβ);
- D = √ (B2 + C2-2B * C * cosβ);
- D = √ (B2 + C2-2B * C * cosα).
3. Τύποι για το μήκος των διαγώνιων ενός ισοσκελούς τραπεζοειδούς.
Υποθέτουμε ότι το A είναι η κάτω βάση, το Β είναι η κορυφή, το D είναι η διαγώνιος, το M είναι η μεσαία γραμμή, το H είναι το ύψος, το P είναι το εμβαδόν του τραπεζοειδούς, τα α και β είναι οι γωνίες μεταξύ των διαγωνίων. Προσδιορίζουμε το μήκος χρησιμοποιώντας τους ακόλουθους τύπους:
- D = √ (Μ2 + Η2);
- D = √ (H2 + (A + B) 2/4);
- D = √ (H (A + B) / sinα) = √ (2P / sinα) = √ (2M * H / sinα).
Για την περίπτωση αυτή, η ισότητα ισχύει: sinα = sinβ.
4. Τύποι για το μήκος της διαγώνιας ως προς τις πλευρές και το ύψος.
Υποθέτουμε ότι το Α είναι η κάτω βάση, το Β είναι η κορυφή, το Γ είναι οι πλευρές, το Δ είναι η διαγώνιος, το Η είναι το ύψος, το α είναι η γωνία στην κάτω βάση.
Προσδιορίζουμε το μήκος χρησιμοποιώντας τους ακόλουθους τύπους:
- D = √ (H2 + (A-P * ctgα) 2);
- D = √ (H2 + (B + P * ctgα) 2);
-D = √ (A2 + C2-2A * √ (C2-H2)).

Ας δούμε τι είναι ενδιαφέρον για αυτό το γεωμετρικό σχήμα. Όπως είπαμε, ένα ορθογώνιο τραπεζοειδές έχει δύο ορθές γωνίες.
Εκτός από τον κλασικό ορισμό, υπάρχουν επίσηςάλλα. Για παράδειγμα, ένα ορθογώνιο τραπεζοειδές είναι ένα τραπεζοειδές με τη μία του πλευρά κάθετη στις βάσεις του. Or μια φιγούρα με ορθές γωνίες στην πλευρική πλευρά. Για αυτόν τον τύπο τραπεζοειδούς, το ύψος είναι ίσο με την πλευρική πλευρά, η οποία είναι κάθετη στις βάσεις. Η μεσαία γραμμή είναι το τμήμα γραμμής που συνδέει τα μεσαία σημεία των δύο πλευρών. Η ιδιότητα του αναφερόμενου στοιχείου είναι ότι είναι παράλληλη με τις βάσεις και είναι ίση με το μισό του αθροίσματός τους.
Τώρα ας ρίξουμε μια ματιά στους βασικούς τύπους,ορίζοντας αυτό το γεωμετρικό σχήμα. Για αυτό, υποθέτουμε ότι τα Α και Β είναι λόγοι. C (κάθετα στις βάσεις) και D - πλευρές ορθογώνιου τραπεζοειδούς, M - μεσαία γραμμή, α - οξεία γωνία, περιοχή P -.
1Η πλευρική πλευρά, κάθετη στις βάσεις, είναι ίση με το ύψος του σχήματος (C = H) και είναι ίση με το γινόμενο του μήκους της δεύτερης πλευρικής πλευράς D και του ημίτονου της γωνίας α με μεγαλύτερη βάση ( C = D * sinα). Επιπλέον, είναι ίσο με το γινόμενο της εφαπτομένης της οξείας γωνίας α και τη διαφορά των βάσεων: C = (A-B) * tgα.
2. Η πλευρική πλευρά D (όχι κάθετη στις βάσεις) είναι ίση με το πηλίκο της διαφοράς μεταξύ Α και Β και συνημίτονο (α) της οξείας γωνίας ή το πηλίκο του ύψους του σχήματος Η και του ημιτόνου του οξεία γωνία: D = (AB) / cos α = C / sinα.
3. Η πλευρά, η οποία είναι κάθετη στις βάσεις, είναι ίση με την τετραγωνική ρίζα της διαφοράς μεταξύ του τετραγώνου D - της δεύτερης πλευράς - και του τετραγώνου της διαφοράς μεταξύ των βάσεων:
C = √ (D2- (A-B) 2).
4. Η πλευρά Δ ενός ορθογώνιου τραπεζοειδούς είναι ίση με την τετραγωνική ρίζα του αθροίσματος του τετραγώνου της πλευράς Γ και το τετράγωνο της διαφοράς μεταξύ των βάσεων του γεωμετρικού σχήματος: D = √ (C2 + (A-B) 2).
5. Η πλευρά του C είναι ίση με το πηλίκο της διαίρεσης του διπλού εμβαδού με το άθροισμα των βάσεών του: C = P / M = 2P / (A + B).
6. Το εμβαδόν καθορίζεται από το προϊόν Μ (η μεσαία γραμμή ενός ορθογώνιου τραπεζοειδούς) από το ύψος ή την πλευρά κάθετη στις βάσεις: P = M * H = M * C.
7. Η πλευρά Γ ισούται με το πηλίκο διαιρέσεως του διπλασιασμένου εμβαδού του σχήματος με το γινόμενο του ημίτονου μιας οξείας γωνίας και το άθροισμα των βάσεών του: C = P / M * sinα = 2P / ((A + Β) * sinα).
8. Τύποι για την πλευρική πλευρά ενός ορθογώνιου τραπεζοειδούς μέσω των διαγωνίων του και τη γωνία μεταξύ τους:
- sinα = sinβ;
- C = (D1 * D2 / (A + B)) * sinα = (D1 * D2 / (A + B)) * sinβ,
όπου D1 και D2 είναι οι διαγώνιες του τραπεζοειδούς. α και β είναι οι γωνίες μεταξύ τους.
9. Τύποι για την πλευρική πλευρά μέσω της γωνίας στην κάτω βάση και άλλες πλευρές: D = (A-B) / cosα = C / sinα = H / sinα.
Δεδομένου ότι ένα τραπεζοειδές με ορθή γωνία είναι μια ειδική περίπτωση ενός τραπεζοειδούς, οι υπόλοιποι τύποι που καθορίζουν αυτά τα σχήματα θα αντιστοιχούν σε ένα ορθογώνιο.

Εάν η συνθήκη λέει ότι ένας κύκλος είναι εγγεγραμμένος σε ορθογώνιο τραπεζοειδές, τότε μπορούν να χρησιμοποιηθούν οι ακόλουθες ιδιότητες:
- το άθροισμα των βάσεων είναι ίσο με το άθροισμα των πλευρών ·
- οι αποστάσεις από την κορυφή του ορθογώνιου σχήματος έως τα σημεία εφαπτομένης του εγγεγραμμένου κύκλου είναι πάντα ίσες ·
- το ύψος του τραπεζοειδούς είναι ίσο με την πλευρική πλευρά, κάθετο στις βάσεις και ίσο με τη διάμετρο του κύκλου ·
- το κέντρο του κύκλου είναι το σημείο στο οποίο τέμνονται οι διχοτόμοι των γωνιών.
- εάν η πλευρική πλευρά διαιρείται με το σημείο της εφαπτομένης σε τμήματα Η και Μ, τότε η ακτίνα του κύκλου είναι ίση με την τετραγωνική ρίζα του προϊόντος αυτών των τμημάτων.
- ένα τετράπλευρο που σχηματίζεται από τα σημεία επαφής, την κορυφή του τραπεζοειδούς και το κέντρο του εγγεγραμμένου κύκλου - αυτό είναι ένα τετράγωνο του οποίου η πλευρά είναι ίση με την ακτίνα.
- το εμβαδόν του σχήματος είναι ίσο με το γινόμενο των βάσεων και το γινόμενο του μισού αθροίσματος των βάσεων στο ύψος του.
Αυτό το θέμα είναι πολύ βολικό για τη μελέτη ακινήτων.αυτό το γεωμετρικό σχήμα. Για παράδειγμα, οι διαγώνιες χωρίζουν το τραπεζοειδές σε τέσσερα τρίγωνα, και τα παρακείμενα στις βάσεις είναι παρόμοια, και στις πλευρές είναι ίσα. Αυτή η δήλωση μπορεί να ονομαστεί ιδιότητα τριγώνων στα οποία ένα τραπεζοειδές διαιρείται με τις διαγώνιές του. Το πρώτο μέρος αυτής της δήλωσης αποδεικνύεται μέσω του σημείου της ομοιότητας σε δύο γωνίες. Για να αποδείξετε το δεύτερο μέρος, είναι προτιμότερο να χρησιμοποιήσετε την παρακάτω μέθοδο.
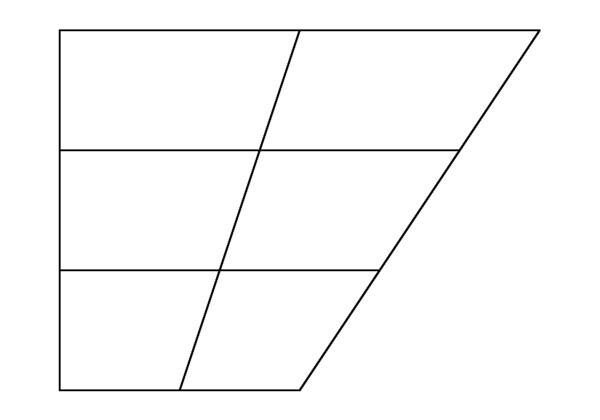
Δεχόμαστε ότι το σχήμα του ABSD (BP και BS είναι τα βασικάτραπεζοειδές) διαιρείται με τις διαγώνιες VD και AC. Το σημείο της τομής τους είναι O. Παίρνουμε τέσσερα τρίγωνα: AOS - στην κάτω βάση, BOS - στην πάνω βάση, ABO και SOD στις πλευρικές πλευρές. Τα τρίγωνα SOD και BFB έχουν κοινό ύψος εάν τα τμήματα BO και OD είναι οι βάσεις τους. Λαμβάνουμε ότι η διαφορά μεταξύ των περιοχών τους (P) είναι ίση με τη διαφορά μεταξύ αυτών των τμημάτων: PBOS / PSOD = BO / OD = K. Επομένως, PSOD = PBOS / K. Ομοίως, τα τρίγωνα BFB και AOB έχουν κοινό ύψος. Παίρνουμε τα τμήματα SB και OA για τις βάσεις τους. Παίρνουμε PBOS / PAOB = SO / OA = K και PAOB = PBOS / K. Από αυτό προκύπτει ότι PSOD = PAOB.
Για την εμπέδωση του υλικού, συνιστώνται οι μαθητέςβρείτε τη σχέση μεταξύ των περιοχών των τριγώνων που προκύπτουν, στα οποία το τραπεζοειδές διαιρείται με τις διαγώνιές του, λύνοντας το ακόλουθο πρόβλημα. Είναι γνωστό ότι οι περιοχές των τριγώνων βιοανάδρασης και AOD είναι ίσες · είναι απαραίτητο να βρεθεί η περιοχή του τραπεζοειδούς. Αφού PSOD = PAOB, σημαίνει ότι PABSD = PBOS + PAOD + 2 * PSOD. Από την ομοιότητα των τριγώνων BFB και AOD προκύπτει ότι BO / OD = √ (PBOS / PAOD). Επομένως, PBOS / PSOD = BO / OD = √ (PBOS / PAOD). Παίρνουμε PSOD = √ (PBOS * PAOD). Τότε PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2.
Συνεχίζοντας την ανάπτυξη αυτού του θέματος, μπορεί κανείς να αποδείξει καιάλλα ενδιαφέροντα χαρακτηριστικά των τραπεζοειδών. Έτσι, με τη βοήθεια της ομοιότητας, μπορεί κανείς να αποδείξει την ιδιότητα ενός τμήματος που διέρχεται από ένα σημείο που σχηματίζεται από τη διασταύρωση των διαγωνίων αυτού του γεωμετρικού σχήματος, παράλληλα με τις βάσεις. Για να γίνει αυτό, θα λύσουμε το ακόλουθο πρόβλημα: είναι απαραίτητο να βρούμε το μήκος του τμήματος RK που διέρχεται από το σημείο Ο. Από την ομοιότητα των τριγώνων AOD και BFB, προκύπτει ότι AO / OS = AD / BS. Από την ομοιότητα των τριγώνων AOR και ASB, προκύπτει ότι AO / AC = RO / BS = HELL / (BS + HELL). Από εδώ παίρνουμε ότι RO = BS * HELL / (BS + HELL). Ομοίως, από την ομοιότητα των τριγώνων DOK και DBS, προκύπτει ότι OK = BS * HELL / (BS + HELL). Από εδώ παίρνουμε ότι RO = OK και RK = 2 * BS * HELL / (BS + HELL). Το τμήμα που διέρχεται από το σημείο τομής των διαγωνίων, παράλληλα με τις βάσεις και συνδέει τις δύο πλευρές, μειώνεται κατά το ήμισυ κατά το σημείο τομής. Το μήκος του είναι ο αρμονικός μέσος όρος της βάσης του σχήματος.
Εξετάστε την ακόλουθη ποιότητα τραπεζοειδούς, η οποίαονομάζεται ιδιότητα τεσσάρων σημείων. Τα σημεία τομής των διαγωνίων (Ο), η τομή της προέκτασης των πλευρικών πλευρών (Ε), καθώς και τα μεσαία σημεία των βάσεων (Τ και Ζ) βρίσκονται πάντα στην ίδια ευθεία. Αυτό αποδεικνύεται εύκολα με τη μέθοδο της ομοιότητας. Τα τρίγωνα που προκύπτουν BES και AED είναι παρόμοια, και σε καθένα από αυτά οι διάμεσοι ET και EZ διαιρούν τη γωνία στην κορυφή E σε ίσα μέρη. Κατά συνέπεια, τα σημεία Ε, Τ και Ж βρίσκονται σε μία ευθεία. Με τον ίδιο τρόπο, τα σημεία T, O και Zh βρίσκονται σε μία ευθεία γραμμή. Όλα αυτά προκύπτουν από την ομοιότητα των τριγώνων BFB και AOD. Από αυτό συμπεραίνουμε ότι και τα τέσσερα σημεία - E, T, O και F - θα βρίσκονται σε μία ευθεία.
Χρησιμοποιώντας τέτοια τραπεζοειδή, μπορεί κανείς να προσφέρειοι μαθητές βρίσκουν το μήκος του τμήματος (LF), το οποίο χωρίζει το σχήμα σε δύο παρόμοια. Αυτό το τμήμα πρέπει να είναι παράλληλο με τις βάσεις. Δεδομένου ότι τα ληφθέντα τραπεζοειδή ALPD και LBSF είναι παρόμοια, τότε BS / LF = LF / BP. Από αυτό προκύπτει ότι LF = √ (BS * HELL). Λαμβάνουμε ότι το τμήμα που χωρίζει το τραπεζοειδές σε δύο παρόμοια έχει μήκος ίσο με το γεωμετρικό μέσο των μηκών των βάσεων του σχήματος.
Εξετάστε την ακόλουθη ιδιότητα ομοιότητας.Βασίζεται σε ένα τμήμα που χωρίζει το τραπεζοειδές σε δύο ίσου μεγέθους σχήματα. Υποθέτουμε ότι το τραπεζοειδές ABSD διαιρείται με το τμήμα ΕΝ σε δύο παρόμοια. Από την κορυφή Β, το ύψος πέφτει, το οποίο διαιρείται με το τμήμα EH σε δύο μέρη - Β1 και Β2. Παίρνουμε: PABSD / 2 = (BS + EH) * B1 / 2 = (HELL + EH) * B2 / 2 και PABSD = (BS + HELL) * (B1 + B2) / 2. Στη συνέχεια, συνθέτουμε ένα σύστημα, του οποίου η πρώτη εξίσωση είναι (BS + EH) * B1 = (AD + EH) * B2 και η δεύτερη (BS + EH) * B1 = (BS + HELL) * (B1 + B2) / 2 Από αυτό προκύπτει ότι B2 / B1 = (BS + EH) / (HELL + EH) και BS + EH = ((BS + HELL) / 2) * (1 + B2 / B1). Λαμβάνουμε ότι το μήκος του τμήματος που χωρίζει το τραπεζοειδές σε δύο ίσα μεγέθη είναι ίσο με το μέσο τετράγωνο ρίζας των μηκών των βάσεων: √ ((BS2 + AD2) / 2).
Έτσι, αποδείξαμε ότι:
1. Το τμήμα που συνδέει τα μεσαία σημεία των πλευρικών πλευρών στο τραπεζοειδές είναι παράλληλο με το BP και το BS και είναι ίσο με τον αριθμητικό μέσο των BS και BP (το μήκος της βάσης του τραπεζοειδούς).
2. Η ευθεία που διέρχεται από το σημείο Ο της τομής των διαγώνιων παράλληλα με την ΚΟΛΥΣΗ και το ΒΣ θα είναι ίση με την αρμονική μέση τιμή των αριθμών ΚΟΛΑΣΗΣ και ΒΣ (2 * BS * HELL / (BS + HELL)).
3. Το τμήμα που χωρίζει το τραπεζοειδές σε παρόμοια έχει το μήκος του γεωμετρικού μέσου όρου των βάσεων του BS και του BP.
4. Το στοιχείο που διαιρεί το σχήμα σε δύο ίσα μεγέθη έχει το μήκος των μέσων τετραγωνικών αριθμών BP και BS.
Για την εμπέδωση του υλικού και την κατανόηση της σύνδεσης μεταξύτα τμήματα που μελετήθηκαν, ο μαθητής πρέπει να τα κατασκευάσει για ένα συγκεκριμένο τραπεζοειδές. Μπορεί εύκολα να εμφανίσει τη μεσαία γραμμή και το τμήμα που διέρχεται από το σημείο Ο - τη διασταύρωση των διαγωνίων του σχήματος - παράλληλα με τις βάσεις. Πού θα βρίσκονται όμως το τρίτο και το τέταρτο; Αυτή η απάντηση θα οδηγήσει τον μαθητή να ανακαλύψει την επιθυμητή σχέση μεταξύ των μέσων όρων.
Εξετάστε την ακόλουθη ιδιότητα αυτού του σχήματος.Υποθέτουμε ότι το τμήμα MH είναι παράλληλο με τις βάσεις και διαιρεί τις διαγώνιες στο μισό. Τα σημεία τομής θα ονομάζονται Ш και Ш. Αυτό το τμήμα θα είναι ίσο με τη μισή διαφορά των βάσεων. Ας ρίξουμε μια πιο προσεκτική ματιά σε αυτό. MSh - η μεσαία γραμμή του τριγώνου ABS, είναι ίση με BS / 2. Το MCh είναι η μεσαία γραμμή του τριγώνου ABD, είναι ίση με BP / 2. Τότε παίρνουμε ότι SHSH = MSH-MSH, επομένως, SHSH = HELL / 2-BS / 2 = (HELL + VS) / 2.
Ας δούμε πώς καθορίζεταιαυτό το στοιχείο για το δεδομένο γεωμετρικό σχήμα. Για να γίνει αυτό, είναι απαραίτητο να επεκτείνετε τις βάσεις σε αντίθετες κατευθύνσεις. Τι σημαίνει? Είναι απαραίτητο να προσθέσετε το κάτω στην επάνω βάση - σε κάθε πλευρά, για παράδειγμα, στα δεξιά. Και επεκτείνετε το κάτω με το μήκος του άνω αριστερά. Στη συνέχεια, τα συνδέουμε με μια διαγώνιο. Το σημείο τομής αυτού του τμήματος με τη μεσαία γραμμή του σχήματος είναι το κέντρο βάρους του τραπεζοειδούς.
Ας απαριθμήσουμε τα χαρακτηριστικά τέτοιων σχημάτων:
1. Ένα τραπεζοειδές μπορεί να εγγραφεί σε κύκλο μόνο αν είναι ισοσκελές.
2. Ένα τραπεζοειδές μπορεί να περιγραφεί γύρω από έναν κύκλο, με την προϋπόθεση ότι το άθροισμα των μηκών των βάσεών τους είναι ίσο με το άθροισμα των μηκών των πλευρικών πλευρών.
Συνέπειες εγγεγραμμένου κύκλου:
1. Το ύψος του περιγραφόμενου τραπεζοειδούς είναι πάντα ίσο με δύο ακτίνες.
2. Η πλευρική πλευρά του περιγραφόμενου τραπεζοειδούς παρατηρείται από το κέντρο του κύκλου σε ορθή γωνία.
Το πρώτο συμπέρασμα είναι προφανές, αλλά για την απόδειξητο δεύτερο, απαιτείται να διαπιστωθεί ότι η γωνία του SOD είναι σωστή, η οποία, στην πραγματικότητα, επίσης δεν θα είναι δύσκολη. Αλλά η γνώση αυτής της ιδιότητας θα σας επιτρέψει να χρησιμοποιήσετε ορθογώνιο τρίγωνο κατά την επίλυση προβλημάτων.
Τώρα ας συγκεκριμενοποιήσουμε αυτές τις συνέπειες γιαένα ισοσκελές τραπεζοειδές που είναι εγγεγραμμένο σε κύκλο. Λαμβάνουμε ότι το ύψος είναι ο γεωμετρικός μέσος όρος της βάσης του σχήματος: H = 2R = √ (BS * HELL). Ενώ εξασκείτε τη βασική τεχνική επίλυσης προβλημάτων για τραπεζοειδή (η αρχή της διατήρησης δύο ύψους), ο μαθητής πρέπει να λύσει την ακόλουθη εργασία. Υποθέτουμε ότι το BT είναι το ύψος της ισοσκελούς μορφής του ABSD. Είναι απαραίτητο να βρεθούν τμήματα AT και TD. Χρησιμοποιώντας τον τύπο που περιγράφεται παραπάνω, δεν θα είναι δύσκολο να γίνει αυτό.
Τώρα ας καταλάβουμε πώς να προσδιορίσουμε την ακτίνακύκλο χρησιμοποιώντας την περιοχή του περιγραμμένου τραπεζίου. Χαμηλώνουμε το ύψος από την κορυφή Β στη βάση της αρτηριακής πίεσης. Δεδομένου ότι ο κύκλος είναι εγγεγραμμένος σε τραπεζοειδές, τότε BS + HELL = 2AB ή AB = (BS + HELL) / 2. Από το τρίγωνο ABN βρίσκουμε sinα = BN / AB = 2 * BN / (BS + HELL). PABSD = (BS + HELL) * BN / 2, BN = 2R. Παίρνουμε PABSD = (BS + HELL) * R, προκύπτει ότι R = PABSD / (BS + HELL).
.

Τώρα ήρθε η ώρα να προχωρήσουμε στο τελευταίο στοιχείο αυτού του γεωμετρικού σχήματος. Ας καταλάβουμε ποια είναι η μεσαία γραμμή του τραπεζοειδούς (Μ):
1. Μέσω των βάσεων: Μ = (Α + Β) / 2.
2. Μέσω ύψους, βάσης και γωνιών:
• Μ = Α-Η * (ctgα + ctgβ) / 2;
• Μ = Β + Η * (ctgα + ctgβ) / 2.
3. Μέσα από το ύψος, τις διαγώνιες και τη γωνία μεταξύ τους. Για παράδειγμα, τα D1 και D2 είναι οι διαγώνιες ενός τραπεζοειδούς. α, β - γωνίες μεταξύ τους:
M = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.
4. Μέσα από την περιοχή και το ύψος: M = P / N.


























