
Avaruudessa taso voidaan asettaa eri tavointapoja (yksi piste ja vektori, kaksi pistettä ja vektori, kolme pistettä jne.). Tämän mielessä tason yhtälöllä voi olla erilaisia muotoja. Lisäksi, jos tietyt ehdot täyttyvät, tasot voivat olla yhdensuuntaisia, kohtisuoria, leikkaavia jne. Puhumme tästä tässä artikkelissa. Opimme laatimaan tason yleisen yhtälön ja paljon muuta.
Oletetaan, että on välilyönti R3, jossa on suorakulmainen XYZ-koordinaattijärjestelmä. Määritetään vektori α, joka vapautuu alkupisteestä O. Piirrä vektorin α pään kautta taso P, joka on kohtisuorassa sitä kohtaan.
Merkitään mielivaltaisessa pisteessä Q = (x, y, z). Allekirjoitetaan piste Q: n sädevektori kirjaimella p. Tässä tapauksessa vektorin a pituus on yhtä suuri kuin p = IaI ja Ʋ = (cosa, cosβ, cosγ).
Tämä on yksikkövektori, joka osoittaasekä vektori a. α, β ja γ ovat kulmia, jotka muodostuvat vektorin Ʋ ja vastaavasti avaruusakselien x, y, z positiivisten suuntien välillä. Minkä tahansa pisteen QϵП projektio vektorille Ʋ on vakioarvo, joka on yhtä suuri kuin p: (p, Ʋ) = p (p ≥0).
Yllä olevalla yhtälöllä on merkitystä, kun p = 0.Ainoa asia on, että taso P tässä tapauksessa leikkaa pisteen O (α = 0), joka on alkupiste, ja pisteestä O annettu yksikkövektori Ʋ on kohtisuorassa P: hen suunnasta huolimatta, mikä tarkoittaa, että vektori determined määritetään tarkka merkki. Edellinen yhtälö on tasomme P yhtälö, joka ilmaistaan vektorimuodossa. Mutta koordinaateissa se näyttää tältä:

P on tässä suurempi tai yhtä suuri kuin 0. Olemme löytäneet avaruuden tason yhtälön normaalimuodossa.
Jos koordinaattien yhtälö kerrotaan millä tahansa luvulla, joka ei ole nolla, saadaan annettua vastaava yhtälö, joka määrittelee saman tason. Se näyttää tältä:

Tässä A, B, C ovat lukuja, jotka ovat samanaikaisesti nollia. Tätä yhtälöä kutsutaan yleiseksi tasoyhtälöksi.
Yhtälöä sen yleisessä muodossa voidaan muuttaa lisäolosuhteiden läsnä ollessa. Tarkastellaan joitain niistä.
Oletetaan, että kerroin A on 0. Tämä tarkoittaa, että tämä taso on yhdensuuntainen annetun akselin Ox kanssa. Tässä tapauksessa yhtälön muoto muuttuu: Vu + Cz + D = 0.
Vastaavasti yhtälön muoto muuttuu seuraavissa olosuhteissa:
Siinä tapauksessa, että luvut A, B, C, D eroavat nollasta, yhtälön muoto (0) voi olla seuraava:
x / a + y / b + z / c = 1,
jossa a = -D / A, b = -D / B, c = -D / C.
Tämän seurauksena saamme tason yhtälön segmentteinä. On syytä huomata, että tämä taso leikkaa Ox-akselin pisteessä, jolla on koordinaatit (a, 0,0), Oy - (0, b, 0) ja Oz - (0,0, c).

Kun otetaan huomioon yhtälö x / a + y / b + z / c = 1, on helppo esittää visuaalisesti tason sijainti suhteessa tiettyyn koordinaatistoon.
Normaalilla vektorilla n tasolle P on koordinaatit, jotka ovat tämän tason yleisen yhtälön kertoimet, eli n (A, B, C).

Normaalin n koordinaattien määrittämiseksi riittää tietää tietyn tason yleinen yhtälö.
Kun käytetään viivasegmenttiyhtälöä, seon muoto x / a + y / b + z / c = 1, koska kun käytetään yleistä yhtälöä, voit kirjoittaa minkä tahansa normaalin vektorin koordinaatit tietylle tasolle: (1 / a + 1 / b + 1 / c).
On syytä huomata, että normaali vektori auttaaratkaista erilaisia ongelmia. Yleisimpiä ongelmia ovat tasojen kohtisuoruuden tai yhdensuuntaisuuden osoittamisen ongelma, tasojen välisten kulmien tai tasojen ja viivojen välisten kulmien löytäminen.
Annettua tasoa kohtisuoraa nollavektoria n kutsutaan normaaliksi (normaaliksi) tietylle tasolle.
Oletetaan, että koordinaattitilassa (suorakulmainen koordinaattijärjestelmä) Oxyz annetaan:

On tarpeen laatia yhtälö tasolle, joka kulkee normaalin n suhteen kohtisuorassa olevan pisteen M2 läpi.
Avaruudessa valitsemme minkä tahansa mielivaltaisen pisteen jamerkitsemme sitä M: llä (xy, z). Olkoon minkä tahansa pisteen M (x, y, z) säteen vektori r = x * i + y * j + z * k, ja pisteen Mₒ (xₒ, yₒ, zₒ) sädevektori - rₒ = xₒ * i + yₒ * j + zₒ * k. Piste M kuuluu tiettyyn tasoon, jos vektori МₒМ on kohtisuorassa vektorin n kanssa. Kirjoita ortogonaalisuuden ehto pistetulolla:
[МₒМ, n] = 0.
Koska МₒМ = r - rₒ, tason vektoriyhtälö näyttää tältä:
[r - rₒ, n] = 0.
Tällä yhtälöllä voi olla toinen muoto.Tätä varten käytetään pistetulon ominaisuuksia ja yhtälön vasen puoli muunnetaan. [r - rₒ, n] = [r, n] - [rₒ, n]. Jos [rₒ, n] merkitään c: ksi, saadaan seuraava yhtälö: [r, n] - c = 0 tai [r, n] = c, joka ilmaisee projektioiden vakauden tasoon kuuluvien annettujen pisteiden normaalivektorivektorissa.
Nyt saat koordinaattimuodon, jolla kirjoitetaan tasojemme vektoriyhtälö [r - rₒ, n] = 0. Koska r - rₒ = (x - xₒ) * i + (y - yₒ) * j + (z - zₒ) * k, ja n = A * i + B * j + C * k, meillä on:

On käynyt ilmi, että meillä on yhtälö tasolle, joka kulkee normaalin n suhteen kohtisuorassa olevan pisteen läpi:
A * (x- xₒ) + B * (y– yₒ) C * (z - zₒ) = 0.
Määritetään kaksi mielivaltaista pistettä M '(x', y ', z') ja M ″ (x ″, y ″, z ″) sekä vektori a (a ′, a ″, a).
Nyt voimme laatia yhtälön tietylle tasolle, joka kulkee olemassa olevien pisteiden M 'ja M' sekä minkä tahansa pisteen M, jonka koordinaatit (x, y, z) ovat yhdensuuntaiset tietyn vektorin a kanssa.
Lisäksi vektorien M′M = {x-x ′; y-y ′; zz ′} ja M ″ M = {x ″ -x ′; y ″ -y ′; z ″ -z ′} on oltava samantasoisia vektorin kanssa a = (a ′, a ″, a ‴), mikä tarkoittaa, että (M′M, M ″ M, a) = 0.
Joten yhtälömme tasossa avaruudessa näyttää tältä:
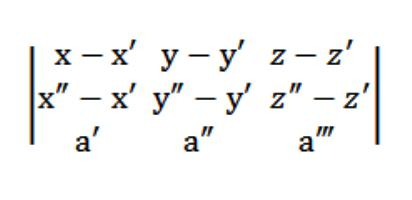
Oletetaan, että meillä on kolme asiaa:(x ′, y ′, z ′), (x ″, y ″, z ″), (x, y ‴, z ‴), jotka eivät kuulu yhteen suoraan. On tarpeen kirjoittaa yhtälö tasolle, joka kulkee annettujen kolmen pisteen läpi. Geometriateoria väittää, että tällaista tasoa on todella olemassa, mutta se on ainoa ja jäljittelemätön. Koska tämä taso leikkaa pisteen (x ′, y ′, z ′), sen yhtälön muoto on seuraava:

Tässä A, B, C ovat nollia samanaikaisesti. Annettu taso leikkaa myös vielä kaksi pistettä: (x ″, y ″, z ″) ja (x ‴, y ‴, z ‴). Tältä osin seuraavien ehtojen on täytyttävä:

Nyt voimme laatia homogeenisen (lineaarisen) yhtälöjärjestelmän tuntemattomilla u, v, w:

Meidän tapauksessamme x, y tai z on mielivaltainenpiste, joka täyttää yhtälön (1). Kun otetaan huomioon yhtälö (1) ja yhtälöjärjestelmä (2) ja (3), yllä olevassa kuvassa esitetty yhtälöjärjestelmä täyttyy vektorilla N (A, B, C), joka ei ole triviaali. Siksi tämän järjestelmän determinantti on yhtä suuri kuin nolla.
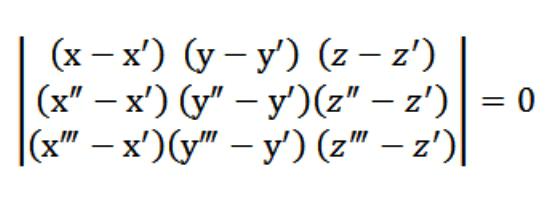
Yhtälö (1), jonka saimme, onon tason yhtälö. Se kulkee tarkasti 3 pisteen läpi, ja se on helppo tarkistaa. Tätä varten meidän on laajennettava determinanttimme ensimmäisellä rivillä olevilla elementeillä. Determinantin olemassa olevista ominaisuuksista seuraa, että tasomme leikkaa samanaikaisesti kolme alun perin määritettyä pistettä (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴). Eli olemme ratkaisseet meille asetetun tehtävän.
Dihedraalinen kulma onspatiaalinen geometrinen kuvio, jonka muodostavat kaksi puolitasoa, jotka lähtevät yhdestä suorasta. Toisin sanoen tämä on osa tilaa, jota nämä puolitasot rajoittavat.
Oletetaan, että meillä on kaksi tasoa seuraavilla yhtälöillä:
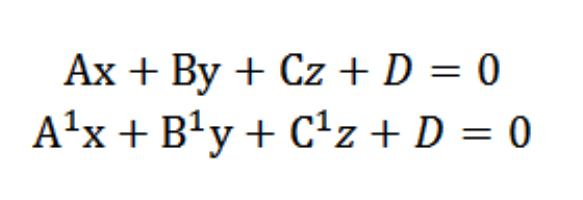
Tiedämme, että vektorit N = (A, B, C) jaN1 = (A1, B1, C1) ovat kohtisuorassa annettujen tasojen mukaan. Tässä suhteessa kulma the vektorien N ja N1 välillä on yhtä suuri kuin kulma (kaksitahoinen), joka on näiden tasojen välillä. Pistetuote on:
NN¹ = | N || N¹ | cosφ,
juuri siksi
cosφ = NN1 / | N || N1 | = (AA1 + BB1 + CC1) / ((√ (A2 + B2 + C2)) * (√ (A1) 2 + (B1) 2 ((C1) 2)).
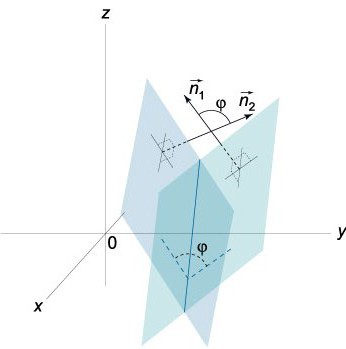
Riittää, kun otetaan huomioon, että 0≤φ≤π.
Itse asiassa kaksi leikkaavaa tasoa muodostavat kaksi kulmaa (kaksisuuntainen): φ1 ja φ2... Niiden summa on yhtä suuri kuin π (φ1+ φ2= π). Kosinien absoluuttiset arvot ovat samat, mutta ne eroavat toisistaan merkkien eli cos φ: n suhteen1= -cos φ2... Jos yhtälössä (0) korvataan A, B ja C vastaavasti numeroilla -A, -B ja -C, niin saatu yhtälö määrittää saman tason, yhtälön ainoan kulman φ cos φ = NN1/ | N || N1| korvataan π-φ: llä.
Tasoja kutsutaan kohtisuoriksi, välilläjonka kulma on 90 astetta. Edellä esitetyn materiaalin avulla voimme löytää tason, joka on kohtisuorassa toiseen. Oletetaan, että meillä on kaksi tasoa: Ax + By + Cz + D = 0 ja A1x + B1y + C1z + D = 0. Voimme väittää, että ne ovat kohtisuorassa, jos cosφ = 0. Tämä tarkoittaa, että NN1 = AA1 + BB1 + CC1 = 0.
Rinnakkaiset ovat kaksi tasoa, jotka eivät sisällä yhteisiä pisteitä.
Ehto tasojen yhdensuuntaisuudelle (niiden yhtälötsama kuin edellisessä osassa) on se, että niihin kohtisuorat vektorit N ja N1 ovat kolineaarisia. Tämä tarkoittaa, että seuraavat suhteellisuusvaatimukset täyttyvät:
A / A1 = B / B1 = C / C1.
Jos suhteellisuusolosuhteita pidennetään - A / A¹ = B / B¹ = C / C¹ = DD¹,
tämä osoittaa, että nämä koneet ovat yhteneviä. Ja tämä tarkoittaa, että yhtälöt Ax + By + Cz + D = 0 ja A1x + B1y + C1z + D1 = 0 kuvaavat yhtä tasoa.
Oletetaan, että meillä on taso P, joka on annettuyhtälö (0). On tarpeen löytää etäisyys siihen pisteestä koordinaateilla (xₒ, yₒ, zₒ) = Qₒ. Tätä varten sinun on saatettava tason P yhtälö normaaliin muotoon:
(p, v) = p (p ≥0).
Tässä tapauksessa ρ (x, y, z) onpisteen Q sädevektori, joka sijaitsee P: llä, p on kohtisuoran P pituus, joka vapautettiin nollapisteestä, v on yksikkövektori, joka sijaitsee suunnassa a.

Jonkin pisteen Q = (x, y, z), joka kuuluu P: hen, samoin kuin annetun pisteen Q sädevektorin ero ρ-ρº0= (xₒ, yₒ, zₒ) on sellainen vektori, jonka projektion absoluuttinen arvo v: llä on yhtä suuri kuin etäisyys d, joka on löydettävä Q: sta0= (xₒ, yₒ, zₒ) - P:
D = | (ρ-ρ0, v) | mutta
(ρ-ρ0, v) = (ρ, v) - (ρ0, v) = р– (ρ0, v).
Joten käy ilmi
d = | (ρ0, v) -p |.
Nyt nähdään laskemaan etäisyys d Q: sta0 tasolle P, sinun on käytettävä tason yhtälön normaalia muotoa siirtäen samalla p: n vasemmalle puolelle ja korvaamalla (xₒ, yₒ, zₒ) viimeisessä x: n, y: n, z: n sijasta.
Täten löydämme tuloksena olevan lausekkeen absoluuttisen arvon, toisin sanoen halutun d: n.
Parametrikielen avulla saamme ilmeisen:
d = | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).
Jos annettu piste Q0 on tason P toisella puolella, kuten alkuperä, sitten vektorin ρ-ρ välissä0 ja v on tylsä kulma, siksi:
d = - (ρ-ρ0, v) = (ρ0, v) -p> 0.
Siinä tapauksessa, että piste Q0 yhdessä koordinaattien alkupisteen kanssa sijaitsee P: n samalla puolella, sitten luotu kulma on terävä, eli:
d = (ρ-ρ0, v) = p - (s0, v)> 0.
Tämän seurauksena käy ilmi, että ensimmäisessä tapauksessa (ρ0, v)> р, toisessa (ρ0, v) <p.
Pinnan tangenttitaso tangenttipisteessä Mº on taso, joka sisältää kaikki mahdolliset tangentit tämän pinnan läpi piirrettyihin käyriin.
Tällä pinnan yhtälön muodolla F (x, y, z) = 0 tangenttitason yhtälö tangenttipisteessä Mº (xº, yº, zº) näyttää tältä:
Fx(xº, yº, zº) (x-xº) + Fx(xº, yº, zº) (y- yº) + Fx(xº, yº, zº) (z-zº) = 0.
Jos asetamme pinnan nimenomaisessa muodossa z = f (x, y), niin tangenttitaso kuvataan yhtälöllä:
z-zº = f (xº, yº) (x-xº) + f (xº, yº) (y-yº).
Järjestelmä sijaitsee kolmiulotteisessa tilassaKoordinaatit (suorakaiteen muotoinen) Oxyz, annetaan kaksi tasoa P 'ja P', jotka leikkaavat eivätkä osu yhteen. Koska mikä tahansa suorakaiteen muotoisen koordinaatiston taso määritetään yleisen yhtälön avulla, oletetaan, että P ′ ja P ″ saadaan yhtälöillä Ax + B′y + C′z + D ′ = 0 ja A ″ x + B ″ y + C ″ z + D ″ = 0. Tässä tapauksessa meillä on P ′ -tason normaali n ′ (A ′, B ′, C ′) ja P ″ -tason normaali n ″ (A ″, B ″, C ″). Koska tasomme eivät ole yhdensuuntaiset eivätkä osu yhteen, nämä vektorit eivät ole kolineaarisia. Matematiikan kielellä voimme kirjoittaa tämän ehdon seuraavasti: n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. Olkoon P ′: n ja P ″: n leikkauspisteessä oleva suora viiva merkitty kirjaimella a, tässä tapauksessa a = P ′ ∩ P ″.
a on suora viiva, joka koostuu joukosta kaikkia pisteitä(yhteiset) tasot P ′ ja P ″. Tämä tarkoittaa, että minkä tahansa suoraan a kuuluvan pisteen koordinaattien on samanaikaisesti täytettävä yhtälöt A'x + B'y + C'z + D '= 0 ja A ″ x + B ″ y + C ″ z + D ″ = 0. Tämä tarkoittaa, että pisteen koordinaatit ovat erityinen ratkaisu seuraavaan yhtälöjärjestelmään:

Seurauksena on, että tämän ratkaisu (yleinen)yhtälöjärjestelmä määrittää kunkin suoran pisteen koordinaatit, jotka toimivat P: n ja P: n leikkauspisteenä, ja määrittää suoran a: n avaruuden Oxyz-koordinaatistossa (suorakaiteen muotoinen).


























