
Un trapèze est un cas particulier d'un quadrilatère, ydont une paire de côtés est parallèle. Le terme «trapèze» vient du mot grec τράπεζα, qui signifie «table», «table». Dans cet article, nous examinerons les types de trapèze et ses propriétés. De plus, nous verrons comment calculer les éléments individuels de cette figure géométrique. Par exemple, la diagonale d'un trapèze isocèle, la ligne médiane, l'aire, etc. Le matériau est présenté dans le style de la géométrie populaire élémentaire, c'est-à-dire sous une forme facilement accessible.
Tout d'abord, voyons ce que c'estquadrilatère. Cette forme est un cas particulier de polygone à quatre côtés et quatre sommets. Deux sommets d'un quadrilatère qui ne sont pas adjacents sont appelés opposés. La même chose peut être dite pour deux côtés non adjacents. Les principaux types de quadrangles sont le parallélogramme, le rectangle, le losange, le carré, le trapèze et le deltoïde.

Donc, revenons aux trapèzes.Comme nous l'avons dit, cette figure a deux côtés parallèles. Ils s'appellent des bases. Les deux autres (non parallèles) sont les côtés. Dans le matériel des examens et des différents tests, vous pouvez très souvent trouver des tâches liées aux trapèzes, dont la solution nécessite souvent que l'étudiant ait des connaissances non prévues par le programme. Le cours de géométrie scolaire présente aux élèves les propriétés des angles et des diagonales, ainsi que la ligne médiane d'un trapèze isocèle. Mais en plus de cela, la figure géométrique mentionnée a d'autres caractéristiques. Mais à leur sujet un peu plus tard ...
Il existe de nombreux types de ce chiffre. Cependant, le plus souvent, il est habituel d'en considérer deux - isocèles et rectangulaires.
1. Un trapèze rectangulaire est une figure dans laquelle l'un des côtés latéraux est perpendiculaire aux bases. Ses deux angles sont toujours égaux à quatre-vingt-dix degrés.
2. Un trapèze isocèle est une figure géométrique dont les côtés sont égaux entre eux. Cela signifie que les angles aux bases sont également égaux par paire.

Le principe principal est l'utilisation del'approche dite basée sur les tâches. En fait, il n'est pas nécessaire d'introduire de nouvelles propriétés de cette figure dans le cours théorique de la géométrie. Ils peuvent être ouverts et formulés dans le processus de résolution de divers problèmes (mieux que ceux du système). Dans le même temps, il est très important que l'enseignant sache quelles tâches doivent être confiées aux écoliers à un moment ou à un autre du processus éducatif. De plus, chaque propriété trapézoïdale peut être représentée comme une tâche clé dans le système de tâches.
Le deuxième principe est le soi-disantorganisation en spirale de l'étude des propriétés «remarquables» du trapèze. Cela implique un retour dans le processus d'apprentissage aux caractéristiques individuelles d'une figure géométrique donnée. Cela permet aux apprenants de les mémoriser plus facilement. Par exemple, la propriété de quatre points. Il peut être prouvé à la fois en étudiant la similitude et en utilisant ensuite des vecteurs. Et la taille égale des triangles adjacents aux côtés latéraux de la figure peut être prouvée en appliquant non seulement les propriétés des triangles de hauteur égale dessinés sur les côtés qui se trouvent sur une ligne droite, mais également en utilisant la formule S = 1/2 (ab * sinα). De plus, vous pouvez travailler sur le théorème des sinus sur un trapèze inscrit ou un triangle rectangle sur un trapèze décrit, etc.
Application de fonctionnalités "hors programme"une figure géométrique dans le contenu d'un cours scolaire est une technologie de tâche pour les enseigner. Un appel constant aux propriétés étudiées lors de la réussite d'autres sujets permet aux étudiants d'acquérir une compréhension plus profonde du trapèze et garantit le succès de la résolution des tâches assignées. Alors passons à l'étude de cette merveilleuse figure.

Comme nous l'avons déjà noté, cette géométrieles chiffres sur les côtés sont égaux. Il est également connu sous le nom de trapèze régulier. Et pourquoi est-il si remarquable et pourquoi a-t-il obtenu un tel nom? Les particularités de cette figure incluent le fait qu'elle a non seulement les côtés et les angles aux bases, mais également les diagonales. De plus, la somme des angles d'un trapèze isocèle est de 360 degrés. Mais ce n'est pas tout! De tous les trapèzes connus, seul un isocèle peut décrire un cercle. Cela est dû au fait que la somme des angles opposés de cette figure est de 180 degrés, et ce n'est que dans cette condition qu'un cercle peut être décrit autour d'un quadrilatère. La propriété suivante de la figure géométrique considérée est que la distance entre le haut de la base et la projection du sommet opposé sur la ligne droite qui contient cette base sera égale à la ligne médiane.
Voyons maintenant comment trouver les angles d'un trapèze isocèle. Considérons une solution à ce problème, à condition que les dimensions des côtés de la figure soient connues.
Habituellement, le quadrilatère est généralement notélettres A, B, C, D, où BS et HELL sont les bases. Dans un trapèze isocèle, les côtés sont égaux. Nous supposerons que leur taille est égale à X et que les tailles des bases sont égales à Y et Z (plus petites et plus grandes, respectivement). Pour effectuer le calcul, il est nécessaire de dessiner la hauteur N. à partir de l'angle B. Le résultat est un triangle rectangle ABN, où AB est l'hypoténuse, et BN et AH sont les jambes. Nous calculons la taille de la jambe AH: soustrayons la plus petite de la plus grande base, et divisons le résultat par 2. Nous l'écrivons sous la forme de la formule: (ZY) / 2 = F. Maintenant, pour calculer l'angle aigu du triangle, nous utilisons la fonction cos. On obtient l'enregistrement suivant: cos (β) = X / F. Nous calculons maintenant l'angle: β = arcos (X / F). De plus, connaissant un angle, nous pouvons déterminer le second, pour cela nous effectuons une opération arithmétique élémentaire: 180 - β. Tous les angles sont définis.
Il existe également une deuxième solution à ce problème.Au début, nous abaissons la hauteur de N. à partir du coin. Calculez la valeur de la jambe BN. On sait que le carré de l'hypoténuse d'un triangle rectangle est égal à la somme des carrés des jambes. On obtient: BN = √ (X2-F2). Ensuite, nous utilisons la fonction trigonométrique tg. En conséquence, nous avons: β = arctan (BN / F). Un coin pointu a été trouvé. Ensuite, nous définissons un angle obtus de la même manière que dans la première méthode.
Tout d'abord, écrivons quatre règles. Si les diagonales d'un trapèze isocèle sont perpendiculaires, alors:
- la hauteur de la figure sera égale à la somme des bases, divisée par deux;
- sa hauteur et sa ligne médiane sont égales;
- l'aire du trapèze sera égale au carré de la hauteur (ligne médiane, la moitié de la somme des bases);
- le carré de la diagonale est égal à la moitié du carré de la somme des bases ou au double du carré de la ligne médiane (hauteur).
Considérons maintenant les formules qui déterminent la diagonale d'un trapèze isocèle. Ce bloc d'informations peut être divisé en quatre parties:
1. Formule de la longueur d'une diagonale en fonction de ses côtés.
Nous supposons que A est la base du bas, B est le haut, C est les côtés égaux, D est la diagonale. Dans ce cas, la longueur peut être déterminée comme suit:
D = √ (C2 + A * B).
2. Formules pour la longueur de la diagonale par le théorème du cosinus.
Nous acceptons que A est la base inférieure, B est la base supérieure,C - côtés égaux, D - diagonale, α (à la base inférieure) et β (à la base supérieure) - angles trapézoïdaux. Nous obtenons les formules suivantes qui peuvent être utilisées pour calculer la longueur de la diagonale:
- D = √ (A2 + C2-2A * C * cosα);
- D = √ (A2 + C2-2A * C * cosβ);
- D = √ (B2 + C2-2B * C * cosβ);
- D = √ (B2 + C2-2B * C * cosα).
3. Formules pour la longueur des diagonales d'un trapèze isocèle.
Nous supposons que A est la base du bas, B est le haut, D est la diagonale, M est la ligne médiane, H est la hauteur, P est l'aire du trapèze, α et β sont les angles entre les diagonales. Nous déterminons la longueur à l'aide des formules suivantes:
- D = √ (M2 + H2);
- D = √ (H2 + (A + B) 2/4);
- D = √ (H (A + B) / sinα) = √ (2P / sinα) = √ (2M * H / sinα).
Dans ce cas, l'égalité est vraie: sinα = sinβ.
4. Formules pour la longueur de la diagonale en termes de côtés et de hauteur.
Nous supposons que A est la base inférieure, B est la base supérieure, C les côtés, D est la diagonale, H est la hauteur, α est l'angle à la base inférieure.
Nous déterminons la longueur à l'aide des formules suivantes:
- D = √ (H2 + (A-P * ctgα) 2);
- D = √ (H2 + (B + P * ctgα) 2);
- D = √ (A2 + C2-2A * √ (C2-H2)).

Regardons ce qui est intéressant à propos de cette figure géométrique. Comme nous l'avons dit, un trapèze rectangulaire a deux angles droits.
En plus de la définition classique, il existe égalementautres. Par exemple, un trapèze rectangulaire est un trapèze avec un côté perpendiculaire à ses bases. Ou une figure avec des angles droits sur le côté latéral. Pour ce type de trapèze, la hauteur est égale au côté latéral, qui est perpendiculaire aux bases. La ligne médiane est le segment de ligne qui relie les milieux des deux côtés. La propriété de l'élément mentionné est qu'il est parallèle aux bases et est égal à la moitié de leur somme.
Jetons maintenant un œil aux formules de base,définissant cette figure géométrique. Pour cela, nous supposons que A et B sont des fondations; C (perpendiculaire aux bases) et D - côtés d'un trapèze rectangulaire, M - ligne médiane, α - angle aigu, P - aire.
une.Le côté latéral, perpendiculaire aux bases, est égal à la hauteur de la figure (C = H), et est égal au produit de la longueur du deuxième côté latéral D par le sinus de l'angle α avec une base plus grande ( C = D * sinα). De plus, il est égal au produit de la tangente de l'angle aigu α par la différence des bases: C = (A-B) * tgα.
2. Le côté latéral D (non perpendiculaire aux bases) est égal au quotient de la différence entre A et B et le cosinus (α) de l'angle aigu ou au quotient de la hauteur de la figure H et du sinus du angle aigu: D = (AB) / cos α = C / sinα.
3. Le côté latéral, qui est perpendiculaire aux bases, est égal à la racine carrée de la différence entre le carré D - le deuxième côté - et le carré de la différence entre les bases:
C = √ (D2- (A-B) 2).
4. Le côté D d'un trapèze rectangulaire est égal à la racine carrée de la somme du carré du côté C et du carré de la différence entre les bases de la figure géométrique: D = √ (C2 + (A-B) 2).
5. Le côté de C est égal au quotient de la division de l'aire double par la somme de ses bases: C = P / M = 2P / (A + B).
6. L'aire est déterminée par le produit M (la ligne médiane d'un trapèze rectangulaire) par la hauteur ou le côté perpendiculaire aux bases: P = M * H = M * C.
7. Le côté C est égal au quotient de la division de l'aire doublée de la figure par le produit du sinus d'un angle aigu et de la somme de ses bases: C = P / M * sinα = 2P / ((A + B) * sinα).
8. Formules pour le côté latéral d'un trapèze rectangulaire passant par ses diagonales et l'angle entre elles:
- sinα = sinβ;
- C = (D1 * D2 / (A + B)) * sinα = (D1 * D2 / (A + B)) * sinβ,
où D1 et D2 sont les diagonales du trapèze; α et β sont les angles entre eux.
9. Formules pour le côté latéral passant par l'angle de la base inférieure et des autres côtés: D = (A-B) / cosα = C / sinα = H / sinα.
Puisqu'un trapèze à angle droit est un cas particulier de trapèze, le reste des formules définissant ces figures correspondra à une forme rectangulaire.

Si la condition indique qu'un cercle est inscrit dans un trapèze rectangulaire, les propriétés suivantes peuvent être utilisées:
- la somme des bases est égale à la somme des côtés;
- les distances entre le haut de la forme rectangulaire et les points de tangence du cercle inscrit sont toujours égales;
- la hauteur du trapèze est égale au côté latéral, perpendiculaire aux bases, et égale au diamètre du cercle;
- le centre du cercle est le point d'intersection des bissectrices des coins;
- si le côté latéral est divisé par le point de tangence en segments H et M, alors le rayon du cercle est égal à la racine carrée du produit de ces segments;
- un quadrilatère formé par les points de contact, le sommet du trapèze et le centre du cercle inscrit - c'est un carré dont le côté est égal au rayon;
- l'aire de la figure est égale au produit des bases par le produit de la demi-somme des bases par sa hauteur.
Ce sujet est très pratique pour étudier les propriétés.cette forme géométrique. Par exemple, les diagonales divisent le trapèze en quatre triangles, et ceux adjacents aux bases sont similaires et les côtés sont égaux. Cette déclaration peut être appelée une propriété de triangles dans laquelle un trapèze est divisé par ses diagonales. La première partie de cet énoncé est prouvée par le signe de similitude sous deux angles. Pour prouver la deuxième partie, il est préférable d'utiliser la méthode ci-dessous.
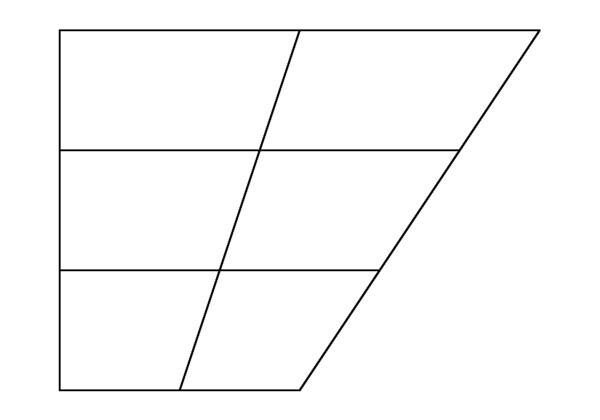
Nous acceptons que le chiffre de l'ABSD (BP et BS sont les basestrapèze) est divisé par les diagonales VD et AC. Le point de leur intersection est O. Nous obtenons quatre triangles: AOS - à la base inférieure, BOS - à la base supérieure, ABO et SOD sur les côtés latéraux. Les triangles SOD et BFB ont une hauteur commune si les segments BO et OD sont leurs bases. On obtient que la différence entre leurs aires (P) est égale à la différence entre ces segments: PBOS / PSOD = BO / OD = K.Par conséquent, PSOD = PBOS / K. De même, les triangles BFB et AOB ont une hauteur commune. Nous prenons les segments SB et OA pour leurs bases. On obtient PBOS / PAOB = SO / OA = K et PAOB = PBOS / K. Il en découle que PSOD = PAOB.
Pour consolider le matériel, il est recommandé aux étudiantstrouver la connexion entre les zones des triangles obtenus, dans lesquels le trapèze est divisé par ses diagonales, résolvant le problème suivant. On sait que les aires des triangles biofeedback et AOD sont égales, il faut trouver l'aire du trapèze. Puisque PSOD = PAOB, cela signifie que PABSD = PBOS + PAOD + 2 * PSOD. De la similitude des triangles BFB et AOD, il s'ensuit que BO / OD = √ (PBOS / PAOD). Par conséquent, PBOS / PSOD = BO / OD = √ (PBOS / PAOD). Nous obtenons PSOD = √ (PBOS * PAOD). Alors PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2.
En continuant à développer ce sujet, on peut prouver etautres caractéristiques intéressantes des trapèzes. Ainsi, à l'aide de la similitude, on peut prouver la propriété d'un segment qui passe par un point formé par l'intersection des diagonales de cette figure géométrique, parallèle aux bases. Pour ce faire, nous allons résoudre le problème suivant: il faut trouver la longueur du segment RK qui passe par le point O. De la similitude des triangles AOD et BFB, il s'ensuit que AO / OS = AD / BS. De la similitude des triangles AOR et ASB, il s'ensuit que AO / AC = RO / BS = HELL / (BS + HELL). De là, nous obtenons que RO = BS * HELL / (BS + HELL). De même, de la similitude des triangles DOK et DBS, il s'ensuit que OK = BS * HELL / (BS + HELL). De là, nous obtenons que RO = OK et RK = 2 * BS * HELL / (BS + HELL). Le segment passant par le point d'intersection des diagonales, parallèle aux bases et reliant les deux côtés, est divisé par deux par le point d'intersection. Sa longueur est la moyenne harmonique de la base de la figure.
Considérez la qualité trapézoïdale suivante, quiest appelée la propriété à quatre points. Les points d'intersection des diagonales (O), l'intersection de l'extension des côtés latéraux (E), ainsi que les milieux des bases (T et G) se trouvent toujours sur la même ligne. Ceci est facilement prouvé par la méthode de la similitude. Les triangles résultants BES et AED sont similaires, et dans chacun d'eux les médianes ET et EZ divisent l'angle au sommet E en parties égales. Par conséquent, les points E, T et Ж se trouvent sur une même ligne droite. De la même manière, les points T, O et Zh sont situés sur une ligne droite, tout cela découle de la similitude des triangles BFB et AOD. De cela, nous concluons que les quatre points - E, T, O et F - se trouveront sur une ligne droite.
En utilisant de tels trapèzes, nous pouvons offrirles élèves trouvent la longueur du segment (LF), qui divise la figure en deux segments similaires. Ce segment doit être parallèle aux bases. Puisque les trapèzes obtenus ALPD et LBSF sont similaires, alors BS / LF = LF / BP. Il s'ensuit que LF = √ (BS * HELL). On obtient que le segment divisant le trapèze en deux semblables a une longueur égale à la moyenne géométrique des longueurs des bases de la figure.
Considérez la propriété de similitude suivante.Il est basé sur un segment qui divise le trapèze en deux figures de taille égale. Nous supposons que le trapèze ABSD est divisé par le segment ЕН en deux similaires. Du haut de B, la hauteur est supprimée, qui est divisée par le segment EH en deux parties - B1 et B2. On obtient: PABSD / 2 = (BS + EH) * B1 / 2 = (HELL + EH) * B2 / 2 et PABSD = (BS + HELL) * (B1 + B2) / 2. Ensuite, nous composons un système dont la première équation est (BS + EH) * B1 = (AD + EH) * B2 et la seconde (BS + EH) * B1 = (BS + HELL) * (B1 + B2) / 2. Il s'ensuit que B2 / B1 = (BS + EH) / (AD + EH) et BS + EH = ((BS + HELL) / 2) * (1 + B2 / B1). On obtient que la longueur du segment divisant le trapèze en deux tailles égales est égale à la racine carrée moyenne des longueurs des bases: √ ((BS2 + AD2) / 2).
Ainsi, nous avons prouvé que:
1. Le segment reliant les milieux des côtés latéraux au trapèze est parallèle à BP et BS et est égal à la moyenne arithmétique de BS et BP (la longueur de la base du trapèze).
2. La droite passant par le point O de l'intersection des diagonales parallèles à HELL et BS sera égale à la moyenne harmonique des nombres de HELL et BS (2 * BS * HELL / (BS + HELL)).
3. Le segment divisant le trapèze en d'autres similaires a la longueur de la moyenne géométrique des bases de BS et BP.
4. L'élément divisant la figure en deux tailles égales a la longueur des nombres carrés moyens de BP et BS.
Pour consolider le matériel et comprendre le lien entreles segments étudiés, l'étudiant doit les construire pour un trapèze spécifique. Il peut facilement afficher la ligne médiane et le segment qui passe par le point O - l'intersection des diagonales de la figure - parallèlement aux bases. Mais où seront situés les troisième et quatrième? Cette réponse amènera l'étudiant à découvrir la relation souhaitée entre les moyennes.
Considérez la propriété suivante de cette figure.Nous supposons que le segment MH est parallèle aux bases et divise les diagonales en deux. Les points d'intersection seront appelés Ш et Ш. Ce segment sera égal à la demi-différence des bases. Regardons cela de plus près. MSh - la ligne médiane du triangle ABS, elle est égale à BS / 2. MCh est la ligne médiane du triangle ABD, elle est égale à BP / 2. Ensuite, nous obtenons que SHSH = MSH-MSH, donc SHSH = HELL / 2-BS / 2 = (HELL + VS) / 2.
Voyons comment c'est déterminécet élément pour la forme géométrique donnée. Pour ce faire, il est nécessaire d'étendre les bases dans des directions opposées. Qu'est-ce que ça veut dire? Il est nécessaire d'ajouter celui du bas à la base supérieure - de chaque côté, par exemple, à droite. Et prolongez celui du bas de la longueur de celui du haut vers la gauche. Ensuite, nous les connectons avec une diagonale. Le point d'intersection de ce segment avec la ligne médiane de la figure est le centre de gravité du trapèze.
Listons les caractéristiques de ces formes:
1. Un trapèze ne peut être inscrit dans un cercle que s'il est isocèle.
2. Un trapèze peut être décrit autour d'un cercle, à condition que la somme des longueurs de leurs bases soit égale à la somme des longueurs des côtés latéraux.
Conséquences du cercle inscrit:
1. La hauteur du trapèze décrit est toujours égale à deux rayons.
2. Le côté latéral du trapèze décrit est observé à partir du centre du cercle à angle droit.
Le premier corollaire est évident, et pour la preuvele second, il est nécessaire d'établir que l'angle du SOD est correct, ce qui, en fait, ne sera pas non plus difficile. Mais la connaissance de cette propriété vous permettra d'utiliser un triangle rectangle lors de la résolution de problèmes.
Maintenant, concrétisons ces conséquences pourun trapèze isocèle inscrit dans un cercle. On obtient que la hauteur est la moyenne géométrique de la base de la figure: H = 2R = √ (BS * HELL). Tout en pratiquant la technique de base de résolution de problèmes pour les trapèzes (le principe de tenir deux hauteurs), l'étudiant doit résoudre la tâche suivante. Nous supposons que BT est la hauteur de la figure isocèle de l'ABSD. Il est nécessaire de trouver les segments AT et TD. En utilisant la formule décrite ci-dessus, il ne sera pas difficile de le faire.
Voyons maintenant comment déterminer le rayoncercle en utilisant la zone du trapèze circonscrit. Nous abaissons la hauteur du haut B à la base de la pression artérielle. Puisque le cercle est inscrit dans le trapèze, alors BS + HELL = 2AB ou AB = (BS + HELL) / 2. A partir du triangle ABN, nous trouvons sinα = BN / AB = 2 * BN / (BS + HELL). PABSD = (BS + ENFER) * BN / 2, BN = 2R. On obtient PABSD = (BS + HELL) * R, il s'ensuit que R = PABSD / (BS + HELL).
.

Il est maintenant temps de passer au dernier élément de cette forme géométrique. Voyons quelle est la ligne médiane du trapèze (M):
1. À travers les bases: M = (A + B) / 2.
2. À travers la hauteur, la base et les coins:
• M = A-H * (ctgα + ctgβ) / 2;
• M = B + H * (ctgα + ctgβ) / 2.
3. Par la hauteur, les diagonales et l'angle entre elles. Par exemple, D1 et D2 sont les diagonales d'un trapèze; α, β - angles entre eux:
M = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.
4. À travers la zone et la hauteur: M = P / N.


























