מאפיינים ושיטות למציאת שורשי משוואה ריבועית

העולם מתוכנן כך שמספר גדול של החלטותהמשימות מצטמצמות למציאת שורשי המשוואה הריבועית. שורשי המשוואות חשובים לתיאור חוקים שונים. זה היה ידוע לסוקרי בבל העתיקה. אסטרונומים ומהנדסים נאלצו גם הם לפתור בעיות כאלה. כבר במאה השישית לספירה, פיתח המדען ההודי אריאבהאטה את היסודות למציאת שורשי המשוואה הריבועית. הנוסחאות רכשו מראה מוגמר במאה ה -19.

מושגים כלליים

אנו מציעים לך להכיר את חוקי היסוד של שוויון ריבועי. באופן כללי ניתן לכתוב שוויון באופן הבא:

אה² + bx + c = 0,

מספר השורשים של המשוואה הריבועית יכול להיות שווה לאחד או שניים. ניתן לבצע ניתוח מהיר תוך שימוש במושג מפלים:

ד = ב² - 4ac

בהתאם לערך המחושב, אנו מקבלים:

• עבור D> 0, ישנם שני שורשים שונים. הנוסחה הכללית לקביעת שורשי המשוואה הריבועית נראית (-b ± √D) / (2a).
• D = 0, במקרה זה השורש הוא אחד ומתאים לערך x = -b / (2a)
• D <0, לערך שלילי של ההפללה, אין פיתרון למשוואה.

הערה: אם המפלה שלילי, למשוואה אין שורשים רק באזור המספרים האמיתיים. אם האלגברה מורחבת למושג שורשים מורכבים, למשוואה יש פיתרון.

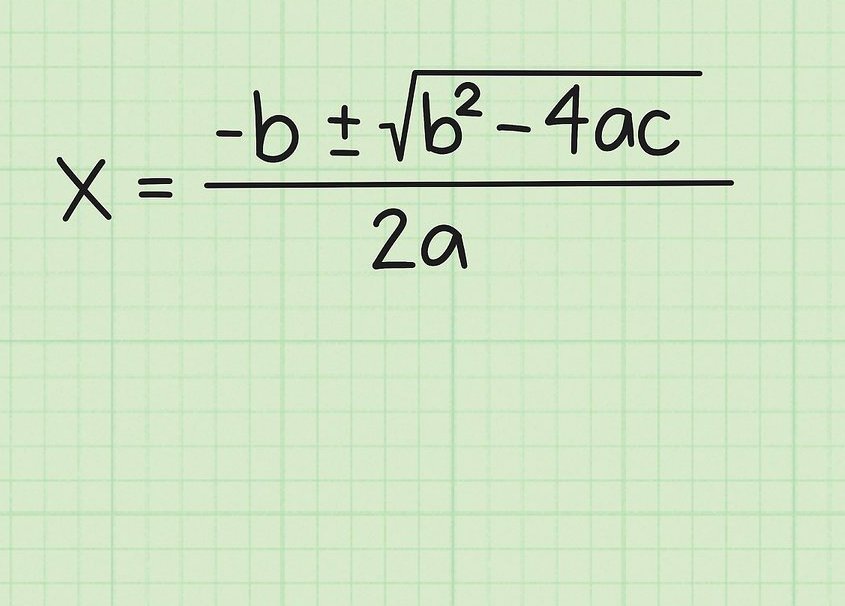
אנו נותנים שרשרת פעולות המאשרת את הנוסחה למציאת השורשים.

מהצורה הכללית של המשוואה נובע כך:

אה² + bx = -c

אנו מכפילים את הצד הימני והשמאלי ב- 4a ומוסיפים b²אנחנו מקבלים

צ'ה²עם² + 4abx + b² = -4ac + b²

אנו הופכים את הצד השמאלי בצורת ריבוע של פולינום (2ax + b)². אנו מחלצים את השורש הריבועי משני צידי המשוואה 2ax + b = -b ± √ (-4ac + b²), אנו מעבירים את המקדם b לצד הימני, אנו מקבלים:

2ax = -b ± √ (-4ac + b²)

להלן:

x = (-b ± √ (ב² - 4ac))

שנדרש להציג.

מקרה מיוחד

במקרים מסוימים ניתן לפשט את הפיתרון לבעיה. לכן, עם מקדם b אפילו אנו מקבלים נוסחה פשוטה יותר.

ציין k = 1 / 2b, ואז הנוסחה הכללית של שורשי המשוואה הריבועית מקבלת את הצורה:

x = (-k ± √ (k² - ac)) / א

עבור D = 0, אנו משיגים x = -k / a

מקרה מסוים אחר הוא פיתרון המשוואה עבור a = 1.

לצפייה x² + bx + c = 0 השורשים יהיו x = -k ± √ (k² - ג) כאשר המפליל גדול מ- 0. במקרה של D = 0, השורש ייקבע על ידי נוסחה פשוטה: x = -k.

באמצעות תרשימים

כל אדם, מבלי לחשוד בכך, נתקל כל העת בתופעות פיזיות, כימיות, ביולוגיות ואפילו חברתיות המתוארות היטב על ידי פונקציה ריבועית.

הערה: עקומה שנבנתה על בסיס פונקציה ריבועית נקראת פרבולה.

הנה כמה דוגמאות.

1. בעת חישוב נתיב הטיסה של הטיל, משתמשים בתכונות התנועה לאורך הפרבולה של גוף המשוחרר בזווית לאופק.
2. המאפיין של פרבולות להפצת העומס באופן שווה נמצא בשימוש נרחב באדריכלות.

בהבנת החשיבות של פונקציה פרבולית, אנו נדע כיצד ללמוד את תכונותיה באמצעות גרף בעזרת המושגים "מפלה" ו"שורשים של משוואה ריבועית ".

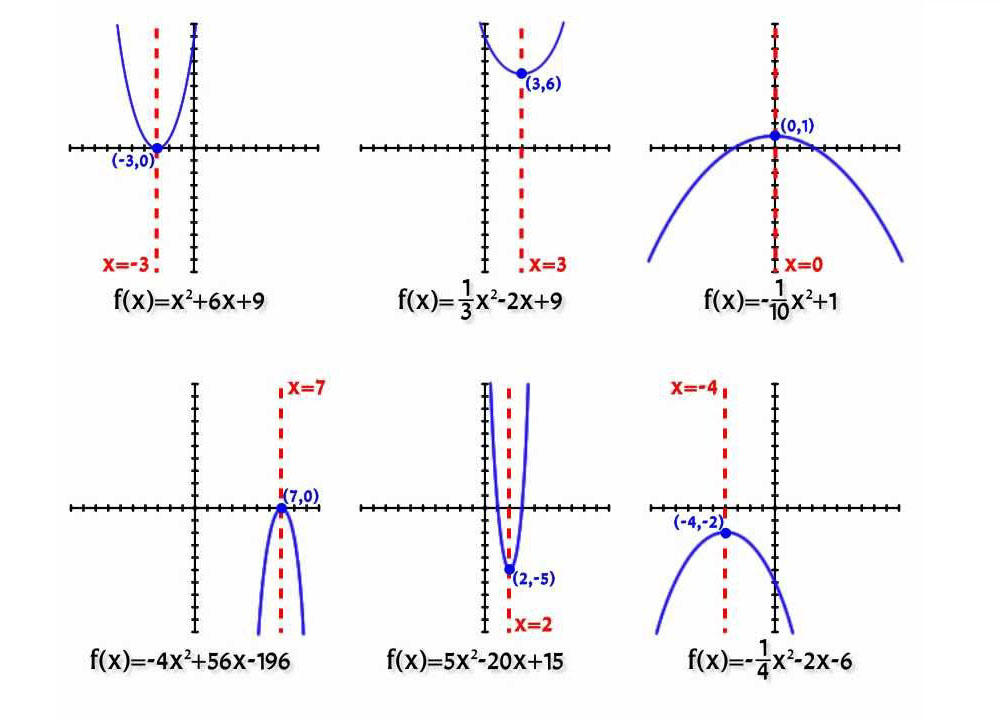
בהתאם לעוצמת המקדמים a ו- b, יש רק שש אפשרויות למיקום העקומה:

1. המפלה חיובי, a ו- b יש סימנים שונים. ענפי הפרבולה מסתכלים למעלה, למשוואה הריבועית שני פתרונות.
2. ההבדל והמקדם b שווים לאפס, המקדם a גדול מאפס. הגרף ממוקם באזור החיובי, למשוואה יש שורש 1.
3. להפללה ולכל המקדמים יש ערכים חיוביים. למשוואה הריבועית אין פיתרון.
4. ההבדל והמקדם a הם שליליים, b גדול מאפס. ענפי הגרף מופנים כלפי מטה, למשוואה יש שני שורשים.
5. ההבדל והמקדם b שווים לאפס, המקדם a שלילי. פרבולה מסתכלת למטה, למשוואה יש שורש אחד.
6. הערכים של המפלה וכל המקדמים הם שליליים. אין פתרונות, ערך הפונקציה נמצא לחלוטין באזור השלילי.

הערה: הווריאציה a = 0 אינה נחשבת, מכיוון שבמקרה זה הפרבולה מתדרדרת לקו ישר.

כל האמור לעיל מאויר היטב על ידי האיור שלהלן.

דוגמאות לפיתרון בעיות

מצב: בעזרת תכונות משותפות, ערכו משוואה ריבועית, ששורשיה שווים זה לזה.

פתרון:

על פי תנאי הבעיה x₁ = x₂, או -b + √ (ב² - 4ac) / (2a) = -b + √ (ב² - 4ac) / (2a). פשט את הערך:

-b + √ (ב² - 4ac) / (2a) - (-b - √ (b² - 4ac) / (2a)) = 0, פתח את הסוגריים ותן מונחים דומים. המשוואה מקבלת צורה 2√ (ב² - 4ac) = 0. הצהרה זו נכונה כאשר b² - 4ac = 0, ומכאן ב² = 4ac ואז הערך b = 2√ (ac) מוחלף למשוואה

אה² + 2√ (ac) x + c = 0, בצורה המופחתת נקבל x² + 2√ (c / a) x + c = 0.

התשובה היא:

עבור a לא שווה ל- 0 ולכל c, יש רק פתרון אחד אם b = 2√ (c / a).

משוואות ריבועיות על כל הפשטות שלהןהם בעלי חשיבות רבה בחישובים הנדסיים. ניתן לתאר כמעט כל תהליך פיזי בקירוב כלשהו באמצעות פונקציות הספק מסדר n. המשוואה הריבועית תהיה הקירוב הראשון שכזה.