
משולש הוא אחת מהדמויות הבסיסיות של פלנטמטריה.זה איתו בתוכנית הלימודים בבית הספר שמתחיל לימוד הגיאומטריה האמיתי, במובן מסוים. בהתאם לסוג הפינות, ניתן לחלק את הדמויות מסוג זה למספר סוגים. כאשר פותרים בעיות, הקל ביותר נחשב בדרך כלל למלבני. מבחינתו ישנם משפטים, כללים רבים, כמו גם פונקציות טריגונומטריות המאפשרות לך למצוא כל רגל או היפוזה, תוך ידיעה בלבד של אורך אחד הצדדים והזווית (כל אחד מלבד הקו הישר).
עם זאת, אם היה קיים רק מין כזהמשולשים, חייהם של תלמידי תיכון ותיכון היו הרבה יותר פשוטים וחסרי דאגות. אבל זה לא כך. לכל דמות שחוקרת הגיאומטריה יש מאפיינים ותכונות משלה. כדי לפתור בביטחון בעיות, עליכם לדעת את המאפיינים של כל המצולעים.

משולש השבילים דומה מאוד לחיית המחמדפיתגורס, שהוזכר במבוא. הכללים הקשורים לבנייתו או למציאת אלמנטים לא ידועים, אפילו תלמיד כיתה ה 'יבין. העיקר הוא לנווט היטב במושגים הבסיסיים של הגיאומטריה ובאלמנטים הבסיסיים של דמויות שטוחות.
מאפיינים של משולש שווה שוקיים צפים החוצהמהמבנה שלה. שתי הפינות בבסיס מצולע כזה זהות, וכך גם הצדדים. מסקנה מסוימת ניתן להסיק ממידע זה. על מנת למצוא את מידת המידה של קודקוד, לדעת את אחת מזוויות הבסיס, עליך להכפיל אותו בשניים ולהחסיר אותו מ -180 מעלות. שני צדדים, שנקודות הקיצון שלהם נמצאים בחלק העליון והתחתון, נקראים לרוחב.
לנתון זה אין כללים ככאלה - הכל נמצאהמשימות נובעות מהקמתה, מה שהופך אותה למובילה ונוחה לתלמידים. עם זאת, קיימת תכונה עיקרית אחת שניתן לכנותה תכונה של חציון משולש שווה שוקיים. הכל קשור לאופי הכפול שלו. אם תבנה משולש כזה על נייר על פי כל הכללים, תבחין שהקו במרכז הוא לא רק החציון, אלא גם הגובה והחציצה.
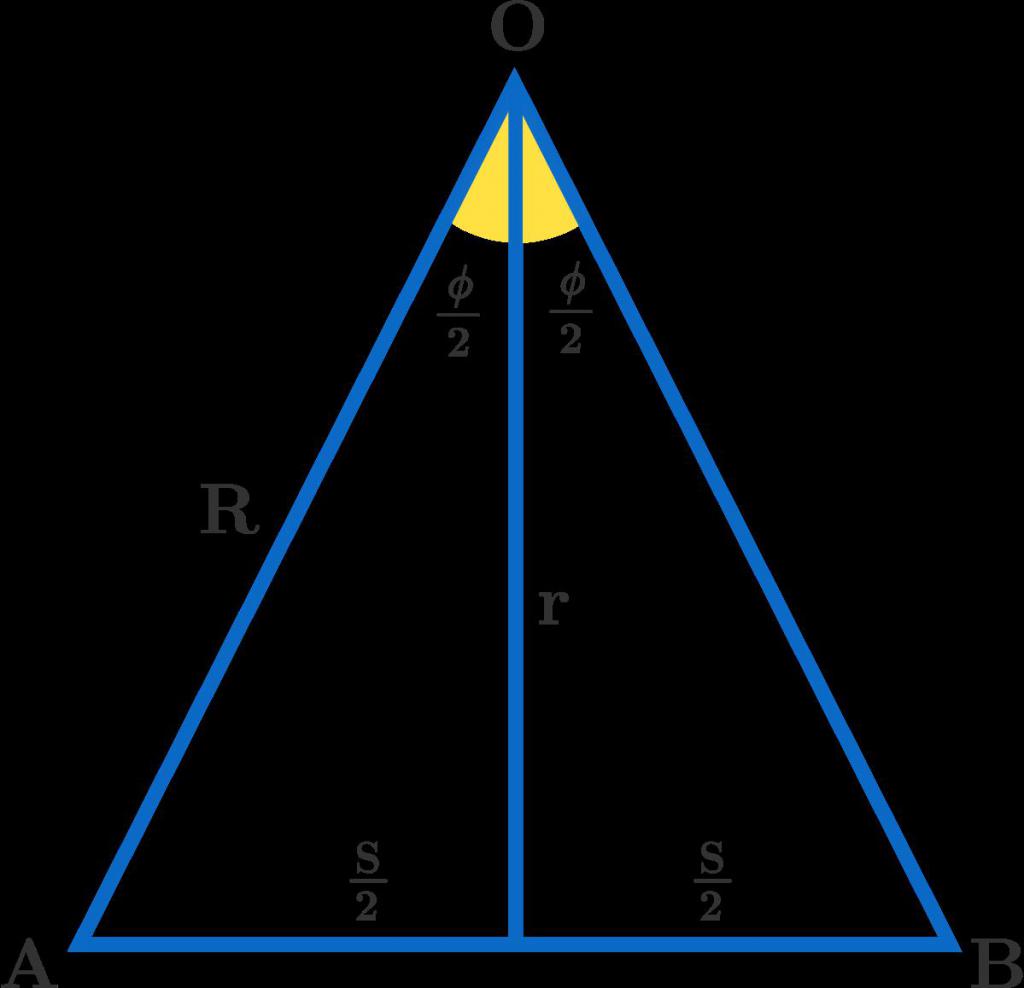
קו ישר משורטט מלמעלה למטהלא יהיה כה חד משמעי. מאפייניו נקבעים על פי המאפיינים העיקריים של משולש שווה שוקיים. בהורדתו מפינת הקודקוד לבסיס, הוא יוצר שני משולשים שווים, ועם הבסיס הוא יוצר בניצב המחלק אותו למקטעים שווים. אין לבלבל סוג משולשים זה עם משולשים שווי צלעות (טעות כזו נעשית לעיתים קרובות על ידי התלמידים). יש להם שלוש פינות זהות, ולא שתיים כמו כאן.


























