
Spręsti daugumą taikomųjų mokslų problemųjums reikia žinoti objekto ar taško vietą, kuri nustatoma naudojant vieną iš patvirtintų koordinatinių sistemų. Be to, yra pakilimo sistemos, kurios taip pat nustato aukščio aukščio vietą Žemės paviršiuje.
Koordinatės - skaitinės arba abėcėlės vertės, sunaudojant kurį galite nustatyti vietą, kurioje taškas yra ant žemės. Todėl koordinačių sistema yra panašių verčių rinkinys, turintis tą patį taško ar objekto paieškos principą.
Būtina rasti taško vietąspręsti daugelį praktinių problemų. Tokiame moksle, kaip geodezija, pagrindinis taškas yra taško nustatymas tam tikroje erdvėje, kurio pasiekimas yra pastatytas.

Dauguma koordinačių sistemų yranustatyti taško vietą plokštumoje, kurią riboja tik dvi ašys. Siekiant nustatyti taško padėtį trimatėje erdvėje, taip pat naudojama aukščių sistema. Su pagalba galite sužinoti tikslią norimo objekto vietą.
Koordinatės sistemos nustato taško vietą ant žemės paviršiaus, suteikdamos jai tris vertes. Jų skaičiavimo principai yra skirtingi kiekvienai koordinačių sistemai.

Pagrindinės geodezijoje naudojamos erdvinės koordinatės:
Visos sistemos turi savo atskaitos tašką, objekto vietos ir apimties vertes.
Pagrindinis skaičius, naudojamas etaloninėms geodezinėms koordinatėms, yra sausumos elipsoidas.
Elipsoidas yra trimatis suspaustas skaičiusgeriausias būdas yra pasaulio vaizdas. Atsižvelgiant į tai, kad pasaulis yra matematiniu požiūriu netaisyklingas skaičius, vietoj to geodezinės koordinatės nustatomos elipsoidu. Tai palengvina daugelio skaičiavimų įgyvendinimą, kad būtų galima nustatyti kūno padėtį ant paviršiaus.

Geodezines koordinates apibrėžia trys vertės: geodezinė platuma, ilguma ir aukštis.
Didesnio tikslumo aukštosios geodezijos uždaviniams spręstibūtina atskirti geodezines ir geografines koordinates. Inžinerinėje geodezijoje naudojamoje sistemoje tokie skirtumai dėl nedidelio darbo užimamo ploto dažniausiai nėra daromi.
Norint nustatyti geodezines koordinateselipsoidas naudojamas kaip atskaitos plokštuma, o geoidas naudojamas geografinėms. Geoidas yra matematiškai netaisyklinga figūra, artimesnė tikrajai Žemės figūrai. Laikoma, kad jo lygus paviršius ramioje būsenoje tęsiasi žemiau jūros lygio.

Geografinė koordinačių sistema, naudojamageodezija, apibūdina taško padėtį erdvėje su trimis vertėmis. Geografinės ilgumos apibrėžimas sutampa su geodeziniu, nes atskaitos taškas taip pat bus pagrindinis dienovidinis, vadinamas Greenwich. Jis eina per to paties pavadinimo observatoriją Londone. Geografinė platuma nustatoma iš pusiaujo, nupiešto ant geoido paviršiaus.
Vietoje naudojamų vietinių koordinačių sistemos aukštisgeodezija, matuojama nuo jūros lygio ramioje būsenoje. Rusijos ir buvusios Sovietų Sąjungos šalių teritorijoje ženklas, pagal kurį nustatomi aukščiai, yra Kronštato potvynio atsargos. Jis yra Baltijos jūros lygyje.
Poliarinė koordinačių sistema, naudojamageodezija, turi kitų matavimų atlikimo niuansų. Jis naudojamas mažuose reljefo plotuose, norint nustatyti santykinę taško vietą. Kilmė gali būti bet koks objektas, pažymėtas kaip kilmė. Taigi, naudojant polines koordinates, neįmanoma nustatyti vienareikšmės taško vietos žemės rutulio teritorijoje.
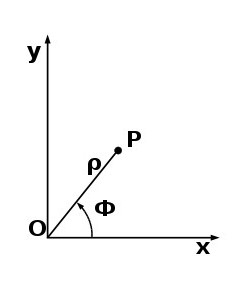
Polines koordinates apibrėžia dvi reikšmės:kampas ir atstumas. Kampas matuojamas nuo šiaurės dienovidinio iki nurodyto taško, nustatant jo padėtį erdvėje. Tačiau vieno kampo nepakaks, todėl įvedamas spindulio vektorius - atstumas nuo stovėjimo taško iki norimo objekto. Šie du parametrai gali būti naudojami vietos taškui surasti.
Paprastai ši koordinačių sistema naudojama inžinerijos darbams, atliekamiems nedideliame reljefo plote, atlikti.
Stačiakampio formos koordinačių sistema, naudojamageodezija taip pat naudojama nedideliuose reljefo plotuose. Pagrindinis sistemos elementas yra koordinačių ašis, iš kurios gaunamas skaičiavimas. Taško koordinatės randamos kaip statmenų, ištrauktų iš abscisės ir koordinačių ašių, ilgis iki norimo taško.

X ašies šiaurės kryptis ir Y ašies rytinė kryptis laikomos teigiamomis, o pietų ir vakarų - neigiama. Atsižvelgiant į ženklus ir ketvirčius, nustatoma taško vieta erdvėje.
Gauso-Krugerio koordinačių zoninė sistema yra panaši į stačiakampę. Skirtumas tas, kad jis gali būti taikomas visoje Žemės rutulio teritorijoje, ne tik mažuose plotuose.
Stačiakampės Gauso-Krugerio zonų koordinatės pagališ tikrųjų jie yra Žemės rutulio projekcija į plokštumą. Praktiniais tikslais atsirado popieriuje pavaizduoti didelius Žemės plotus. Perkėlimo iškraipymas laikomas nereikšmingu.
Pagal šią sistemą Žemės rutulys yra padalintas į ilgumą į šešių laipsnių zonas, kurių viduryje yra ašinis dienovidinis. Pusiaujas yra centre išilgai horizontalios linijos. Dėl to yra 60 tokių zonų.

Kiekviena iš šešiasdešimties zonų turi savostačiakampių koordinačių sistema, išmatuota iš ašinio dienovidinio X ir abscisės iš žemės pusiaujo Y atkarpos. Norėdami unikaliai nustatyti vietą viso Žemės rutulio teritorijoje, zonos numeris dedamas priešais X ir Y reikšmės.
X ašies vertės Rusijoje paprastai yrayra teigiami, o Y reikšmės gali būti neigiamos. Kad abscisės ašies reikšmėse būtų išvengta minuso ženklo, kiekvienos zonos ašinis dienovidinis paprastai perkeliamas 500 metrų į vakarus. Tada visos koordinatės tampa teigiamos.
Koordinačių sistemą pasiūlė Gaussas kaip įmanoma, o XX a. Viduryje matematiškai apskaičiavo Krugeris. Nuo tada jis buvo naudojamas geodezijoje kaip vienas pagrindinių.
Koordinatės ir pakilimo sistemos, naudojamosgeodezija naudojama tiksliai nustatyti taško padėtį Žemėje. Absoliutus aukštis matuojamas nuo jūros lygio ar kito paviršiaus, kuris yra atskaitos taškas. Be to, yra santykinis aukštis. Pastarieji yra skaičiuojami kaip perteklius nuo norimo taško iki kito. Juos patogu naudoti dirbant vietinėje koordinačių sistemoje, siekiant supaprastinti tolesnį rezultatų apdorojimą.
Be to, kas išdėstyta pirmiau, yra ir kitųgeodezijoje naudojamos koordinačių sistemos. Kiekvienas iš jų turi savo privalumų ir trūkumų. Taip pat yra darbo sričių, kurioms svarbus vienas ar kitas vietos nustatymo metodas.
Kurias sistemas lemia darbo tikslasgeriausiai tinka geodezijoje naudojamos koordinatės. Darbui mažose teritorijose patogu naudoti stačiakampes ir polines koordinačių sistemas, o didelio masto problemoms spręsti reikalingos sistemos, leidžiančios aprėpti visą žemės paviršiaus teritoriją.


























