
De geschiedenis van de stelling van Pythagoras kent verschillendemillennia. De bewering dat het kwadraat van de hypotenusa gelijk is aan de som van de vierkanten van de benen, was lang voor de geboorte van de Griekse wiskundige bekend. De stelling van Pythagoras, de scheppingsgeschiedenis en de bewijzen ervan zijn echter voor het merendeel verbonden met deze wetenschapper. Volgens sommige bronnen was de reden hiervoor het eerste bewijs van de stelling, die werd gegeven door Pythagoras. Sommige onderzoekers weerleggen dit feit echter.

Voordat je vertelt hoe het verhaalStelling van Pythagoras, kort stilstaan bij de biografie van een wiskundige. Hij leefde in de VI eeuw voor Christus. De geboortedatum van Pythagoras wordt beschouwd als 570 v.Chr. e., de plaats is het eiland Samos. Er is weinig bekend over het leven van de wetenschapper. Biografische gegevens in oude Griekse bronnen zijn verweven met voor de hand liggende fictie. Op de pagina's van de verhandelingen lijkt hij een grote wijze te zijn, die perfect het woord beheerst en het vermogen om te overtuigen. Trouwens, daarom kreeg de Griekse wiskundige de bijnaam Pythagoras, dat wil zeggen 'overtuigende spraak'. Volgens een andere versie werd de geboorte van de toekomstige wijze voorspeld door Pythia. Haar vader noemde de jongen Pythagoras.

De wijze leerde van de grote geesten van die tijd.Onder de leraren van de jonge Pythagoras zijn Germodamant en Feriqid van Syros. De eerste bracht hem liefde voor muziek bij, de tweede onderwees filosofie. Beide wetenschappen blijven zijn hele leven in de aandacht van de wetenschapper.
Volgens een versie, een nieuwsgierige jongeman,Pythagoras verliet zijn thuisland. Hij ging op zoek naar kennis in Egypte, waar hij, volgens verschillende bronnen, van 11 tot 22 jaar oud verbleef en vervolgens werd gevangengenomen en naar Babylon werd gestuurd. Pythagoras kon profiteren van zijn positie. Gedurende 12 jaar studeerde hij wiskunde, geometrie en magie in een oude staat. Pythagoras keerde pas op 56-jarige leeftijd terug naar Samos. Hier heerste de tiran Policrates op dat moment. Pythagoras kon een dergelijk politiek systeem niet accepteren en ging al snel naar het zuiden van Italië, waar de Griekse kolonie Croton was gevestigd.
Vandaag is het onmogelijk om met zekerheid te zeggen of Pythagoras in Egypte en Babylon was. Misschien verliet hij Samos later en ging rechtstreeks naar Croton.

De geschiedenis van de stelling van Pythagoras houdt verband met de ontwikkeling vangemaakt door de Griekse filosoofschool. Deze religieuze en ethische broederschap predikte een speciale levensstijl, studeerde rekenkunde, geometrie en astronomie, bestudeerde de filosofische en mystieke aspecten van getallen.
Alle ontdekkingen van studenten Griekse wiskundetoegeschreven aan hem. De geschiedenis van de opkomst van de stelling van Pythagoras wordt door oude biografen echter alleen geassocieerd met de filosoof zelf. Er wordt aangenomen dat hij de in Babylon en Egypte opgedane kennis aan de Grieken heeft doorgegeven. Er is ook een versie waarin hij echt een stelling ontdekte over de relatie tussen benen en hypotenusa, niet wetende over de prestaties van andere landen.
In sommige oude Griekse bronnende vreugde van Pythagoras wordt beschreven toen hij de stelling kon bewijzen. Ter ere van deze gebeurtenis bestelde hij een offer aan de goden in de vorm van honderd stieren en maakte een feestmaal. Sommige geleerden wijzen echter op de onmogelijkheid van een dergelijke daad vanwege de eigenaardigheden van de opvattingen van Pythagoras.
Er wordt aangenomen dat in de verhandeling "Begin" is gemaaktEuclid, de auteur geeft een bewijs van de stelling, waarvan de auteur de grote Griekse wiskundige was. Deze weergave werd echter niet door iedereen ondersteund. Zo wees de oude neoplatonische filosoof Proclus erop dat de auteur van het bewijs dat in de 'Elementen' wordt gegeven, Euclides zelf is.
Hoe het ook zij, maar de eerste die de stelling formuleerde, was nog steeds niet Pythagoras.

Stelling van Pythagoras waarvan de scheppingsgeschiedenisbeschouwd in het artikel, volgens de Duitse wiskundige Cantor, was bekend al in 2300 voor Christus. e. in Egypte. De oude inwoners van de Nijlvallei tijdens het bewind van farao Amenemkhet kende ik gelijkheid 32 + 4² = 5². Er wordt aangenomen dat met behulp van driehoeken met zijden 3, 4 en 5 de Egyptische "kabelspanners" rechte hoeken bouwden.
Ze kenden de stelling van Pythagoras in Babylon.Op kleitabletten die teruggaan tot 2000 voor Christus en daterend uit het bewind van koning Hammurabi, werd een geschatte berekening van de hypotenusa van een rechthoekige driehoek ontdekt.
De geschiedenis van de stelling van Pythagoras houdt verband met het oudebeschavingen van India en China. De verhandeling "Zhou-bi Xuan Jin" bevat aanwijzingen dat de Egyptische driehoek (de zijden corresponderen met 3: 4: 5) in de XII eeuw in China bekend was. BC. e., en tot de VI eeuw. BC. e. wiskundigen van deze staat kenden de algemene vorm van de stelling.
De constructie van de rechte hoek met behulp van de Egyptische driehoek werd ook beschreven in het Indiase traktaat "Sulva Sutra", daterend uit de 7e-5e eeuw. BC. e.
De geschiedenis van de stelling van Pythagoras ten tijde van de geboorte van de Griekse wiskundige en filosoof bedroeg dus enkele honderden jaren.
Tijdens zijn bestaan is de stelling één gewordenvan fundamenteel in geometrie. De geschiedenis van het bewijs van de stelling van Pythagoras begon waarschijnlijk met een beschouwing van een gelijkzijdige rechthoekige driehoek. Op zijn hypotenusa en benen zijn vierkanten gebouwd. Degene die "groeide" op hypotenusa zal bestaan uit vier driehoeken gelijk aan de eerste. De vierkanten op de benen bestaan in dit geval uit twee van dergelijke driehoeken. Een eenvoudig grafisch beeld toont duidelijk de geldigheid van de verklaring geformuleerd in de vorm van de beroemde stelling.
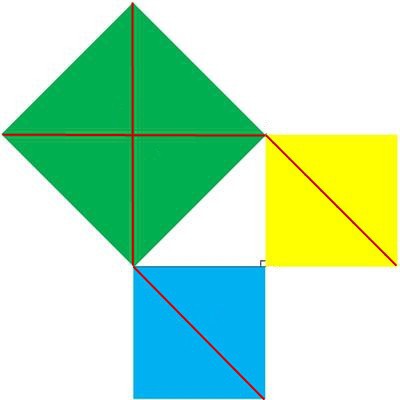
Een ander eenvoudig bewijs combineertgeometrie met algebra. Vier identieke rechthoekige driehoeken met zijden a, b, c zijn zo getekend dat ze twee vierkanten vormen: de buitenste met zijde (a + b) en de binnenste met zijde c. In dit geval is het gebied van het kleinere vierkant gelijk aan2. Het gebied van de grote wordt berekend uit de som van de gebieden van het kleine vierkant en alle driehoeken (het gebied van een rechthoekige driehoek, recall, wordt berekend met de formule (a * c) / 2), d.w.z.2 + 4 * ((a * b) / 2), wat gelijk is aan2 + 2av. De oppervlakte van een groot vierkant kan op een andere manier worden berekend - als het product van twee kanten, dat wil zeggen (a + c)2die gelijk is aan a2 + 2av + c2. Het blijkt:
en2 + 2av + c2 = s2 + 2av,
en2 + in2 = s2.
Er zijn veel opties om dit te bewijzen.Stelling. Euclid en Indiase wetenschappers en Leonardo da Vinci werkten aan hen. Vaak brachten oude wijzen tekeningen, waarvan voorbeelden hierboven staan, en vergezelden ze geen enkele uitleg, behalve de opmerking "Kijk!" De eenvoud van het geometrische bewijs, mits enige kennis beschikbaar was, vereiste geen commentaar.
De geschiedenis van de stelling van Pythagoras, samengevat inartikel, waarin de mythe van zijn oorsprong wordt ontkracht. Het is echter moeilijk om je zelfs voor te stellen dat de naam van de grote Griekse wiskundige en filosoof er op een dag niet meer mee geassocieerd zal worden.


























