Eigenschappen en methoden voor het vinden van de wortels van een kwadratische vergelijking

De wereld is zo ontworpen dat een groot aantal beslissingentaken worden gereduceerd tot het vinden van de wortels van de kwadratische vergelijking. De wortels van de vergelijkingen zijn belangrijk voor het beschrijven van verschillende patronen. Dit was bekend bij de landmeters van het oude Babylon. Astronomen en ingenieurs werden ook gedwongen dergelijke problemen op te lossen. Al in de 6e eeuw na Christus ontwikkelde de Indiase wetenschapper Ariabhata de basis voor het vinden van de wortels van de kwadratische vergelijking. De formules kregen in de 19e eeuw een afgewerkte look.

Algemene concepten

We raden u aan om vertrouwd te raken met de basiswetten van kwadratische gelijkheden. Over het algemeen kan gelijkheid als volgt worden geschreven:

Oh² + bx + c = 0,

Het aantal wortels van de kwadratische vergelijking kan gelijk zijn aan één of twee. Een snelle analyse kan worden gedaan met behulp van het concept van discriminanten:

D = b² - 4ac

Afhankelijk van de berekende waarde krijgen we:

• Voor D> 0 zijn er twee verschillende wortels. De algemene formule voor het bepalen van de wortels van de kwadratische vergelijking ziet eruit als (-b ± √D) / (2a).
• D = 0, in dit geval is de wortel één en komt overeen met de waarde x = -b / (2a)
• D <0, voor een negatieve waarde van de discriminant is er geen oplossing voor de vergelijking.

Opmerking: als de discriminant negatief is, heeft de vergelijking geen wortels alleen in het gebied van reële getallen. Als de algebra wordt uitgebreid tot het concept van complexe wortels, dan heeft de vergelijking een oplossing.

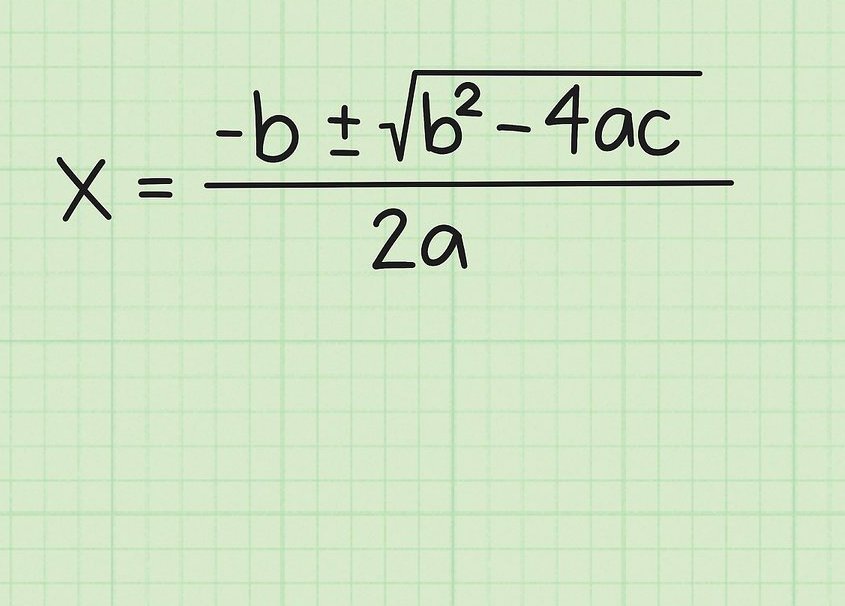
We geven een reeks acties die de formule bevestigen om de wortels te vinden.

Uit de algemene vorm van de vergelijking volgt:

Oh² + bx = -c

We vermenigvuldigen de rechter- en linkerkant met 4a en voegen b toe²we krijgen

cha²met² + 4abx + b² = -4ac + b²

We transformeren de linkerkant in de vorm van een vierkant van een polynoom (2ax + b)². We halen de vierkantswortel uit beide zijden van de vergelijking 2ax + b = -b ± √ (-4ac + b²), we brengen de coëfficiënt b over naar de rechterkant, we krijgen:

2ax = -b ± √ (-4ac + b²)

Dit houdt in:

x = (-b ± √ (b² - 4ac))

Wat nodig was om te laten zien.

Speciaal geval

In sommige gevallen kan de oplossing voor het probleem worden vereenvoudigd. Dus met een nog coëfficiënt b krijgen we een eenvoudigere formule.

Geeft k = 1 / 2b aan, dan krijgt de algemene formule van de wortels van de kwadratische vergelijking de vorm:

x = (-k ± √ (k² - ac)) / a

Voor D = 0 krijgen we x = -k / a

Een ander bijzonder geval is de oplossing van de vergelijking voor a = 1.

Voor weergave x² + bx + c = 0 de wortels zijn x = -k ± √ (k² - c) als de discriminant groter is dan 0. In het geval dat D = 0, wordt de wortel bepaald door een eenvoudige formule: x = -k.

Grafieken gebruiken

Elke persoon, zonder het zelfs maar te vermoeden, komt voortdurend fysieke, chemische, biologische en zelfs sociale verschijnselen tegen die goed worden beschreven door een kwadratische functie.

Let op: een curve die is opgebouwd op basis van een kwadratische functie wordt een parabool genoemd.

Hier zijn enkele voorbeelden.

1. Bij het berekenen van de vliegroute van het projectiel wordt de eigenschap van beweging langs de parabool van een lichaam dat onder een hoek ten opzichte van de horizon vrijkomt, gebruikt.
2. De eigenschap van parabolen om de belasting gelijkmatig te verdelen, wordt veel gebruikt in de architectuur.

We begrijpen het belang van een parabolische functie en gaan uitzoeken hoe we de eigenschappen ervan kunnen bestuderen met behulp van een grafiek met de concepten 'discriminant' en 'wortels van een kwadratische vergelijking'.

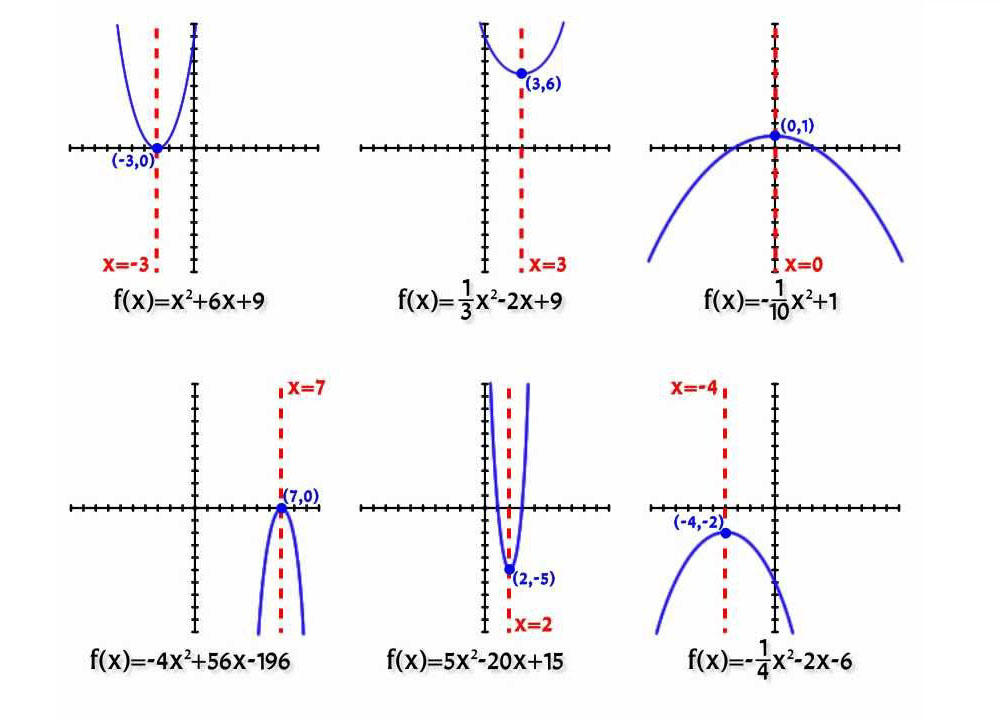
Afhankelijk van de grootte van de coëfficiënten a en b zijn er slechts zes opties voor de positie van de curve:

1. De discriminant is positief, a en b hebben verschillende tekens. De takken van de parabool kijken omhoog, de kwadratische vergelijking heeft twee oplossingen.
2. De discriminant en coëfficiënt b zijn gelijk aan nul, de coëfficiënt a is groter dan nul. De grafiek bevindt zich in de positieve zone, de vergelijking heeft 1 wortel.
3. De discriminant en alle coëfficiënten hebben positieve waarden. De kwadratische vergelijking heeft geen oplossing.
4. De discriminant en coëfficiënt a zijn negatief, b is groter dan nul. De takken van de grafiek zijn naar beneden gericht, de vergelijking heeft twee wortels.
5. De discriminant en de coëfficiënt b zijn gelijk aan nul, de coëfficiënt a is negatief. Parabola kijkt naar beneden, de vergelijking heeft één wortel.
6. De waarden van de discriminant en alle coëfficiënten zijn negatief. Er zijn geen oplossingen, de waarde van de functie ligt volledig in de negatieve zone.

Let op: de variant a = 0 wordt niet overwogen, omdat in dit geval de parabool degenereert tot een rechte lijn.

Al het bovenstaande wordt goed geïllustreerd door de onderstaande afbeelding.

Voorbeelden van het oplossen van problemen

Voorwaarde: maak met behulp van gemeenschappelijke eigenschappen een kwadratische vergelijking, waarvan de wortels gelijk zijn aan elkaar.

Oplossing:

door de toestand van probleem x₁ = x₂, of -b + √ (b² - 4ac) / (2a) = -b + √ (b² - 4ac) / (2a). Vereenvoudig de invoer:

-b + √ (b² - 4ac) / (2a) - (-b - √ (b² - 4ac) / (2a)) = 0, open de haakjes en geef vergelijkbare termen. De vergelijking heeft de vorm 2√ (b² - 4ac) = 0. Deze bewering is waar als b² - 4ac = 0, dus b² = 4ac, dan wordt de waarde b = 2√ (ac) vervangen door de vergelijking

Oh² + 2√ (ac) x + c = 0, in de gereduceerde vorm krijgen we x² + 2√ (c / a) x + c = 0.

Het antwoord is:

voor a niet gelijk aan 0 en c is er maar één oplossing als b = 2√ (c / a).

Kwadratische vergelijkingen voor al zijn eenvoudzijn van groot belang bij technische berekeningen. Vrijwel elk fysiek proces kan met enige benadering worden beschreven met behulp van powerfuncties van orde n. De kwadratische vergelijking zal de eerste dergelijke benadering zijn.