
In de wereld van vandaag gebruiken we steeds meereen verscheidenheid aan auto's en gadgets. En niet alleen wanneer het nodig is om letterlijk onmenselijke kracht te gebruiken: om de lading te verplaatsen, naar een hoogte te tillen, een lange en diepe geul te graven, enz. Auto's verzamelen vandaag robots, multicookers koken voedsel en rekenmachines voeren elementaire rekenkundige berekeningen uit. We horen steeds vaker de uitdrukking 'Booleaanse algebra'. Misschien is de tijd gekomen om de rol van de mens bij het maken van robots en het vermogen van machines om niet alleen wiskundige, maar ook logische problemen op te lossen, te begrijpen.
Vertaald uit het Grieks, is logicaeen geordend denksysteem dat relaties tussen gegeven omstandigheden creëert en ons in staat stelt conclusies te trekken op basis van aannames en aannames. Heel vaak vragen we elkaar: "Is het logisch?" Het ontvangen antwoord bevestigt onze veronderstellingen of bekritiseert de gedachtegang. Maar het proces stopt niet: we blijven redeneren.
Soms is het aantal voorwaarden (inleidend) zogeweldig, en de relatie tussen hen is zo verwarrend en complex dat het menselijk brein niet alles in één keer kan 'verteren'. Het kan meer dan een maand (week, jaar) duren om te begrijpen wat er gebeurt. Maar het moderne leven geeft ons niet zulke tijdsintervallen voor besluitvorming. En we nemen onze toevlucht tot computers. En dit is waar de algebra van de logica verschijnt, met zijn eigen wetten en eigenschappen. Nadat we alle initiële gegevens hebben gedownload, stellen we de computer in staat alle relaties te herkennen, tegenstrijdigheden te elimineren en een bevredigende oplossing te vinden.

De beroemdste Gottfried Wilhelm Leibnizformuleerde het concept van "wiskundige logica", waarvan de taken alleen toegankelijk waren voor een beperkt aantal wetenschappers. Dit gebied veroorzaakte niet veel belangstelling, en tot het midden van de XIX eeuw wisten maar weinigen wiskundige logica.
Grote belangstelling voor de wetenschappelijke gemeenschap is gewekteen geschil waarin de Engelsman George Bull zijn voornemen aankondigde om een tak van wiskunde te creëren die absoluut geen praktische toepassing heeft. Zoals we uit de geschiedenis herinneren, was de industriële productie in die tijd actief in ontwikkeling, er werden allerlei hulpmachines en werktuigmachines ontwikkeld, dat wil zeggen alle wetenschappelijke ontdekkingen hadden een praktische oriëntatie.
Vooruitkijkend zeggen we dat Booleaanse algebra het meest gebruikte onderdeel van de wiskunde in de moderne wereld is. Dus verloor Boule zijn argumentatie.
Сама личность автора заслуживает отдельного aandacht. Zelfs rekening houdend met het feit dat mensen in het verleden ouder werden dan wij, is het nog steeds onmogelijk om niet op te merken dat J. Bull op 16-jarige leeftijd les gaf op een dorpsschool en op 20-jarige leeftijd zijn eigen school opende in Lincoln. De wiskundige sprak vloeiend vijf vreemde talen en las in zijn vrije tijd de werken van Newton en Lagrange voor. En dit alles gaat over de zoon van een eenvoudige arbeider!

In 1839 stuurde Boole voor het eerst zijn wetenschappelijkewerk in het Cambridge Mathematical Journal. De wetenschapper werd 24 jaar oud. Het werk van Boole was zo geïnteresseerd in de leden van de Royal Scientific Society dat hij in 1844 een medaille ontving voor zijn bijdrage aan de ontwikkeling van wiskundige analyse. Een paar meer gepubliceerde werken die de elementen van de wiskundige logica beschreven, lieten de jonge wiskundige professor aan het Cork County College worden. Bedenk dat Buhl zelf geen opleiding had.
In principe is de Booleaanse algebra heel eenvoudig.Er zijn uitspraken (logische uitdrukkingen) die vanuit het oogpunt van wiskunde slechts in twee woorden kunnen worden gedefinieerd: "waarheid" of "onwaar". In het voorjaar bloeien bomen bijvoorbeeld - waar, in de zomer sneeuwt het - een leugen. De hele charme van deze wiskunde is dat het niet strikt noodzakelijk is om alleen cijfers te gebruiken. Voor propositionele algebra zijn uitspraken met een ondubbelzinnige betekenis redelijk geschikt.
Таким образом, алгебра логики может быть letterlijk overal gebruikt: bij het plannen en schrijven van instructies, het analyseren van tegenstrijdige informatie over gebeurtenissen en het bepalen van de volgorde van acties. Het belangrijkste is om te begrijpen dat het volkomen onbelangrijk is hoe we de waarheid of onwaarheid van de verklaring hebben bepaald. Van deze 'hoe' en 'waarom' moet je abstraheren. Waar het om gaat, is slechts een feitelijke verklaring: waar-onwaar.
Natuurlijk zijn functies belangrijk voor programmerenalgebra's van logica, die worden geschreven door de bijbehorende tekens en symbolen. En om ze te leren, moet je een nieuwe vreemde taal leren. Niets is onmogelijk.
Zonder de diepte in te gaan, zullen we ons bezighouden met terminologie. Dus, Booleaanse algebra impliceert de aanwezigheid van:
Verklaringen zijn alle bevestigende uitdrukkingen,die niet op twee plaatsen kan worden geïnterpreteerd. Ze zijn geschreven in de vorm van cijfers (5> 3) of zijn geformuleerd in de gebruikelijke woorden (de olifant is het grootste zoogdier). Bovendien heeft de zinsnede "de giraf heeft geen nek" ook bestaansrecht, alleen de Booleaanse algebra zal hem definiëren als "vals".
Alle verklaringen moeten ondubbelzinnig zijnkarakter, maar ze kunnen elementair en samengesteld zijn. Deze laatste gebruiken logische connectieven. Dat wil zeggen, in de algebra van oordelen worden samengestelde verklaringen gevormd door elementaire toe te voegen door middel van logische bewerkingen.

We herinneren ons al dat operaties in de algebra van proposities zijnlogisch. Net zoals de algebra van getallen rekenkundige bewerkingen gebruikt om getallen op te tellen, af te trekken of te vergelijken, kunt u met de elementen van de wiskundige logica complexe uitspraken doen, een ontkenning geven of het eindresultaat berekenen.
Logische bewerkingen voor formalisering en eenvoudzijn geschreven in formules die we in rekenkunde kennen. De eigenschappen van Booleaanse algebra maken het mogelijk om vergelijkingen te schrijven en onbekenden te berekenen. Logische bewerkingen worden meestal geschreven met behulp van een waarheidstabel. De kolommen definiëren de elementen van berekeningen en de bewerking die erop wordt uitgevoerd, en de rijen tonen het resultaat van de berekeningen.
Meest voorkomend in Booleaanse algebraoperaties zijn negatie (NOT) en logische AND en OR. Vrijwel alle handelingen in de algebra van oordelen kunnen op deze manier worden beschreven. Laten we elk van de drie bewerkingen in meer detail bestuderen.
Negatie (niet) is van toepassing op slechts éénelement (operand). Daarom wordt de negatieoperatie unair genoemd. Gebruik de volgende symbolen om het concept "niet A" te schrijven: ¬A, A¯¯¯ of! A. In tabelvorm ziet het er als volgt uit:
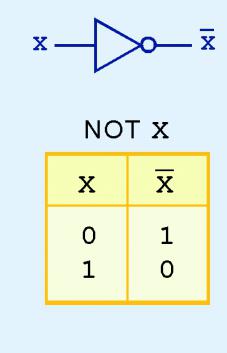
De negatiefunctie wordt gekenmerkt door de volgende stelling: als A waar is, dan is A onwaar. De maan draait bijvoorbeeld om de aarde - waar; De aarde draait om de maan - een leugen.
Logische EN wordt conjunctiebewerking genoemd. Wat betekent het? Ten eerste dat het kan worden toegepast op twee operanden, dat wil zeggen, AND is een binaire bewerking. Ten tweede dat alleen als beide operanden waar zijn (zowel A als B) de uitdrukking zelf waar is. Het spreekwoord "Geduld en werk zullen alles vermalen" suggereert dat alleen beide factoren een persoon zullen helpen om met moeilijkheden om te gaan.
De volgende symbolen worden gebruikt om te schrijven: A∧Б, A⋅Б of A && B.
Conjunctie is analoog aan vermenigvuldiging in rekenkunde. Soms zeggen ze het - logische vermenigvuldiging. Als we de elementen van de tabel met rijen vermenigvuldigen, krijgen we een resultaat dat lijkt op logisch denken.
Disjunctie is een logische OF-bewerking. Het krijgt de waarde van de waarheid als ten minste een van de uitspraken waar is (A of B). Het is als volgt geschreven: A∨B, A + B of A || B. De waarheidstabellen voor deze bewerkingen zijn:
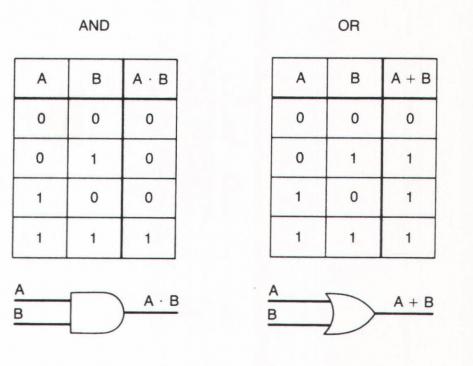
Disjunctie is als rekenkundige optelling. De logische optelbewerking heeft slechts één beperking: 1 + 1 = 1. Maar we onthouden dat de wiskundige logica in digitaal formaat beperkt is tot 0 en 1 (waarbij 1 waar is, 0 is onwaar). De uitspraak "in een museum kun je een meesterwerk zien of een interessante gesprekspartner ontmoeten" betekent bijvoorbeeld dat je kunstwerken kunt zien, of dat je een interessant persoon kunt ontmoeten. Tegelijkertijd is de mogelijkheid van gelijktijdig optreden van beide gebeurtenissen niet uitgesloten.
Dus we weten al wat logische bewerkingenmaakt gebruik van booleaanse algebra. Functies beschrijven alle eigenschappen van elementen van wiskundige logica en stellen u in staat complexe samengestelde probleemomstandigheden te vereenvoudigen. Het meest begrijpelijke en eenvoudigste lijkt de eigenschap te zijn dat afgeleide bewerkingen worden afgewezen. Derivaten betekenen exclusieve OR, implicatie en gelijkwaardigheid. Omdat we ons alleen vertrouwd hebben gemaakt met de basisbewerkingen, zullen we ook alleen de eigenschappen ervan in overweging nemen.
Associativiteit betekent dat in uitspraken als "A, B en C" de volgorde van opsomming van operanden er niet toe doet. De formule zal het als volgt schrijven:
(A∧Б) ∧В = A∧ (БВ) = A∧Б∧В,
(A∨B) ∨V = A∨ (B∨V) = A∨B∨V.
Zoals je kunt zien, is dit niet alleen kenmerkend voor conjunctie, maar ook voor disjunctie.

Commutativiteit stelt dat het resultaat van conjunctie of disjunctie niet afhankelijk is van welk element als eerste werd beschouwd:
A∧B = B∧A; A∨B = B∨A.
Distributiviteit stelt u in staat haakjes uit te breiden in complexe logische uitdrukkingen. De regels zijn vergelijkbaar met haakjesuitbreiding voor vermenigvuldigen en optellen in de algebra:
A∧ (B∨V) = A∧Б∨A∧В; A∨Б∧В = (A∨Б) ∧ (A∨В).
Een en nul eigenschappen, die een van de operanden kan zijn, zijn ook analoog aan algebraïsche vermenigvuldiging met nul of één en optellen met één:
A∧0 = 0, A∧1 = A; A∨0 = A, A∨1 = 1.
Idempotentie vertelt ons dat als relatief ten opzichte van tweevan gelijke operanden, het resultaat van de operatie vergelijkbaar blijkt te zijn, dan kun je onnodige operanden "weggooien", wat het redeneren bemoeilijkt. Zowel conjunctie als disjunctie zijn idempotente bewerkingen.
B∧B = B; B∨B = B.
Absorptie stelt ons ook in staat om de vergelijkingen te vereenvoudigen. Swallowing stelt dat wanneer een andere bewerking op hetzelfde element wordt toegepast op een uitdrukking met één operand, het resultaat de operand is van de slikoperatie.
A∧Б∨Б = B; (A∨B) ∧B = B.
De volgorde van bewerkingen heeft een belangrijkewaarde. Wat de algebra betreft, is er eigenlijk een prioriteit van functies die worden gebruikt door Booleaanse algebra. Formules kunnen alleen worden vereenvoudigd als het belang van de bewerkingen in acht wordt genomen. Rangschikking van meest significant tot onbeduidend, we krijgen de volgende volgorde:
1. Ontkenning.
2. Conjunctie.
3. Disjunctie, exclusief OR.
4. Implicatie, gelijkwaardigheid.
Zoals je kunt zien, hebben alleen negatie en conjunctie geen gelijke prioriteiten. En de prioriteit van disjunctie en exclusieve OR zijn gelijk, evenals de prioriteiten van implicatie en gelijkwaardigheid.
Zoals we al hebben gezegd, gebruiken wiskundige logica en de theorie van algoritmen naast logische basisbewerkingen ook afgeleiden. De meest gebruikte implicaties en equivalenties.
Implicatie, of logisch volgend, iseen verklaring waarin de ene handeling een voorwaarde is en de andere een gevolg van de uitvoering ervan. Met andere woorden, dit is een zin met het voorzetsel "als ... dan". "Hou je van rijden, hou je van sleeën." Dat wil zeggen, om te skiën moet je de slee de heuvel op spannen. Als er geen wens is om de berg af te dalen, dan is het niet nodig om een slee te dragen. Het is als volgt geschreven: A → B of A⇒B.
Equivalentie gaat ervan uit dat het resulterendede actie vindt alleen plaats als beide operanden waar zijn. De nacht maakt bijvoorbeeld plaats voor dag wanneer (en alleen wanneer) de zon boven de horizon opkomt. In de taal van de wiskundige logica is deze verklaring als volgt geschreven: A≡B, A⇔B, A == B.
De algebra van oordelen ontwikkelt zich, en veelgeïnteresseerde wetenschappers formuleerden nieuwe wetten. De bekendste zijn de postulaten van de Schotse wiskundige O. de Morgan. Hij merkte en definieerde eigenschappen als close-negatie, complement en dubbele negatie.
Sluit ontkenning gaat ervan uit dat er geen ontkenning voor het haakje staat: niet (A of B) = niet A of NIET B.
Wanneer de operand wordt ontkend, ongeacht zijn waarde, spreekt men van toevoeging:
B = B = 0; B∨¬B = 1.
En tenslotte tweemaal nee compenseert zichzelf. Die. vóór de operand verdwijnt ofwel de negatie, of blijft er slechts één over.
Wiskundige logica impliceert vereenvoudiginggegeven vergelijkingen. Net als in de algebra, moet je eerst de conditie zoveel mogelijk verzachten (complexe invoer en bewerkingen ermee wegwerken), en dan op zoek gaan naar het juiste antwoord.
Wat kan er worden gedaan om te vereenvoudigen?Converteer alle afgeleide bewerkingen naar eenvoudige bewerkingen. Vouw vervolgens alle haakjes uit (of omgekeerd, plaats ze buiten de haakjes om dit element in te korten). De volgende stap is het toepassen van de eigenschappen van Booleaanse algebra in de praktijk (absorptie, eigenschappen nul en één, etc.).

Uiteindelijk zou de vergelijking moeten bestaan uithet minimum aantal onbekenden gecombineerd door eenvoudige bewerkingen. De gemakkelijkste manier om een oplossing te vinden, is wanneer u veel afwijzingen krijgt. Dan verschijnt het antwoord alsof het vanzelf is.


























