Hvordan oppfører en kondensator seg i en vekselstrømskrets?

Hvis vekselstrømskilden er tilkoblettil motstanden, så vil strømmen og spenningen i kretsen på et hvilket som helst tidspunkt i tidsskjemaet være proporsjonal med hverandre. Dette betyr at strøm- og spenningskurvene vil nå en “topp” verdi samtidig. På denne måten sier vi at strøm og spenning er i fase.

Vi vurderer nå hvordan en kondensator i en vekselstrømskrets vil oppføre seg.

Hvis koblet til en vekselstrømskildekondensator, vil den maksimale verdien på spenningen på den være proporsjonal med den maksimale verdien av strømmen som strømmer i kretsen. Toppbølgespennings sinusoid vil imidlertid ikke oppstå samtidig med maksimal strøm.

I dette eksemplet når øyeblikkelig strømav sin maksimale verdi et kvarter (90 grader) tidligere enn spenningen gjør. I dette tilfellet sier de at "strømmen er 90 ° foran spenningen."

I motsetning til situasjonen i DC-kretsen,V / I-verdien er ikke konstant her. Imidlertid er forholdet V max / I max en veldig nyttig mengde og i elektroteknikk kalles komponentens kapasitans (Xc). Siden denne verdien fremdeles reflekterer forholdet mellom spenning og strøm, dvs. i fysisk forstand er motstand, dens måleenhet er Ohm. Verdien Xc for kondensatoren avhenger av dens kapasitans (C) og frekvensen av vekselstrømmen (f).

Siden kondensatoren i vekselstrømskretsenrms spenningsverdi påføres, strømmer den samme vekselstrømmen i denne kretsen, som er begrenset av kondensatoren. Denne begrensningen skyldes reaktansen fra kondensatoren.

Derfor bestemmes gjeldende verdi i en krets som ikke inneholder andre komponenter bortsett fra kondensatoren av en alternativ versjon av Ohms lov

og_RMS = Y_RMS / X_C

Hvor u_RMS - rms (effektiv) spenningsverdi. Legg merke til at X_med erstatter verdien av R i versjonen av Ohms lov for likestrøm.

Nå ser vi at kondensatoren i kretsenAC oppfører seg ganske annerledes enn en konstant motstand, og situasjonen her er følgelig mer komplisert. For bedre å forstå prosessene som skjer i en slik kjede, er det nyttig å introdusere et slikt konsept som en vektor.

Hovedideen til vektoren er ideen om atat den komplekse verdien av et tidsvarierende signal kan representeres som produktet av et komplekst antall (som ikke er avhengig av tid) og et visst komplekst signal, som er en funksjon av tiden.

For eksempel kan vi representere funksjonen A cos (2πνt + θ) ganske enkelt som en kompleks konstant A ∙ e^jΘ .

Siden vektorer er representert med styrke (eller modul) og vinkel, er de grafisk representert av en pil (eller vektor) som roterer i XY-planet.

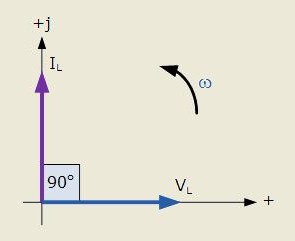
Gitt det faktum at spenningen over kondensatoren"Forsinket" med hensyn til strømmen, vektorene som representerer dem er lokalisert i det komplekse planet som vist på figuren over. I denne figuren roterer strøm- og spenningsvektorene i motsatt retning av bevegelsen med klokken.

I vårt eksempel skyldes strømmen på kondensatorenperiodisk lading. Siden kondensatoren i vekselstrømskretsen med jevne mellomrom kan akkumulere og utlade elektrisk ladning, mellom den og strømkilden, er det en konstant utveksling av energi, som i elektroteknikk kalles reaktiv.