
Datavitenskap som vitenskap om innsamlingsmetoder,bestilling og behandling av forskjellige data begynner utviklingen i midten av det tjuende århundre. Selv om noen historikere mener at dannelsen av informatikk begynte på 1600-tallet, med oppfinnelsen av den første mekaniske kalkulatoren, assosierer de fleste det med tiden for mer avansert databehandling. På 40-tallet av 1900-tallet, med ankomsten av de første datamaskinene, fikk informatikk en ny drivkraft i utvikling.
Det var med ankomsten av de første datamaskinenedet var behov for å utvikle nye metoder for systematisering, beregning og behandling av store datamengder, samt å utvikle algoritmer som ville tillate bruk av det fulle potensialet til nye datamaskiner. Informatikk fikk status som en uavhengig vitenskapelig disiplin og flyttet fra planen for matematiske beregninger til studiet av beregning generelt.

All moderne informatikk er basert pålogiske operasjoner. De kan kalles en grunnleggende komponent. Ved programmering av datasystemer er begrepet en logisk operasjon en slags handling, hvoretter et nytt konsept eller mening genereres, som dannes på grunnlag av eksisterende begreper. Settet med slike handlinger kan variere avhengig av prosessorelementet som må utføre kommandoene. Imidlertid er det noen operasjoner som er felles for nesten alle eksisterende systemer. Dette er operasjoner som arbeider med innholdet i selve verdiene, for eksempel negasjon, eller de som endrer et kvantitativt trekk ved et konsept - tillegg, subtraksjon, multiplikasjon, deling.
Siden algebra av logikk innebærer arbeid medabstrakte konsepter, deretter generaliserte datatyper fungerer som operander for alle logiske operasjoner. De klassiske elementene som proposisjonell algebra fungerer med er proposisjoner, falske eller sanne. I elektronikk og programmering brukes booleanere sant og usant, eller heltallverdiene 1 (sant) og 0 (usant), for å beskrive disse begrepene. Kombinasjonen av disse verdiene, uansett hvor utrolig det måtte høres ut, er bundet til arbeidet med de mest komplekse og store systemene. All programkode som kjøres på en datamaskin eller en hvilken som helst digital enhet, oversettes dynamisk til en sekvens av en eller flere nuller - en universell kode som kan behandles av hvilken som helst prosessor.
Som nevnt tidligere, i klassikerenBoolsk algebra er det to typer funksjoner. Grunnleggende logiske operasjoner på binære datatyper er handlinger som påvirker utsagnet i seg selv (unary, or unary, operation). Dette inkluderer også operasjoner som genererer nye utsagn basert på eksisterende verdier (binære operasjoner, eller toplasser). Rekkefølgen på logiske operasjoner er den samme som når du utfører matematiske beregninger: fra venstre til høyre, inkludert parenteser.

Den mest enkle og en av de mest kjenteBoolsk logikkfunksjon er negasjonsfunksjonen. Denne enkleste logiske operasjonen er motsatt av inngangsoperand. I elektronikk kalles denne handlingen også noen ganger inversjon. Hvis du for eksempel inverterer dommen "sann", er resultatet "usant." Omvendt vil negering av verdien "falsk" resultere i verdien "sann". En slik logisk operasjon i programmering brukes veldig ofte til å forgrense algoritmer og implementere "valget" av det neste settet med instruksjoner basert på resultatene som allerede er tilgjengelige eller endrede forhold.
Brukes i programmering og informatikkbegrenset sett med binære (binære) operasjoner. De får navnet sitt fra det latinske ordet bi, som betyr "to", og er en slags funksjon som tar to argumenter som input og returnerer en ny verdi som et resultat. Sannhetstabeller brukes til å beskrive alle funksjonene til boolsk algebra.
Dette systemet er samlet for en spesifikkantall inngangsoperander og beskriver alle resulterende verdier som en gitt logisk operasjon kan returnere for et gitt sett med inngangsparametere.
De mest brukte funksjonene innen informatikk og databehandling er logisk tillegg (disjunksjon) og logisk multiplikasjon (konjunksjon).
Den logiske OG-operasjonen er en valgfri funksjonden minste av to eller n inngangsoperander. Ved inngangen kan denne funksjonen ha to (binær funksjon), tre verdier (ternær) eller et ubegrenset antall operander (n-ary-operasjon). Når du vurderer funksjonens resultat, vil det være den minste av de medfølgende inngangsverdiene.
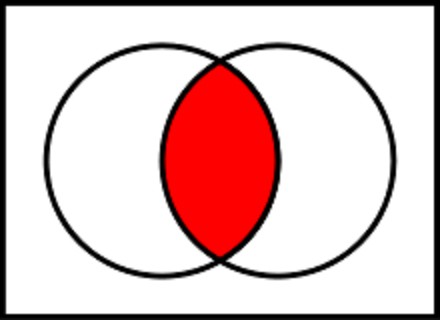
En analog i vanlig algebra er funksjonenmultiplikasjon. Derfor kalles kombinasjonsoperasjonen ofte logisk multiplikasjon. Når du skriver en funksjon, er tegnet enten multiplikasjonstegn (prikk) eller ampersant. Hvis du setter sammen en sannhetstabell for denne funksjonen, vil du se at funksjonen får verdien "sann", eller 1, bare hvis alle inngangsoperandene er sanne. Hvis minst en av inngangsparametrene er lik null, eller verdien er "falsk", vil resultatet av funksjonen også være "falsk".

Dette gjenspeiler analogien med aritmetisk multiplikasjon:å multiplisere et tall og et sett med tall med 0 vil alltid returnere 0. Denne logiske operasjonen er kommutativ: rekkefølgen den mottar inngangsparametrene vil ikke påvirke det endelige resultatet av beregningen.
En annen egenskap ved denne funksjonen erassosiativitet, eller kombinasjon. Denne egenskapen gjør det mulig å ignorere beregningsrekkefølgen når du beregner en sekvens av binære operasjoner. Derfor er det ikke nødvendig å vurdere parentes for 3 eller flere sekvensielle logiske multiplikasjonsoperasjoner. I programmeringen brukes denne funksjonen ofte for å sikre at spesifikke kommandoer bare utføres når et sett med visse betingelser er oppfylt.
Logisk operasjon "ELLER" - en slags boolsk funksjon,som er analogt med algebraisk tillegg. Andre navn på denne funksjonen er logisk tillegg, disjunksjon. Akkurat som en logisk multiplikasjonsoperasjon, kan en disjunksjon være binær (beregne en verdi basert på to argumenter), ternær eller n-ary.

Sannhetstabell for en gitt logisk operasjoner et slags alternativ til sammenheng. Den logiske ELLER-operasjonen beregner maksimalt resultat blant de angitte argumentene. Disjunction tar verdien "false" ved utgangen, eller 0 bare hvis alle inngangsparametre kommer med verdiene 0 ("false"). I alle andre tilfeller vil utdataene være "true", eller 1. For å skrive denne funksjonen brukes oftest det matematiske tegnet på tillegg ("pluss") eller to vertikale striper. Det andre alternativet er vanlig i de fleste programmeringsspråk og er å foretrekke fordi det lar deg tydelig skille en logisk operasjon fra en aritmetisk.
Grunnleggende logiske operasjoner, uansett om de erbinære, ternære eller andre funksjoner er underlagt visse regler og egenskaper som beskriver deres oppførsel. En av slike grunnleggende egenskaper som de ovenfor beskrevne logiske funksjonene har er kommutativitet.

Denne egenskapen sørger for at permutasjonensteder for operander vil ikke verdien av funksjonen endres. Ikke alle operasjoner har denne eiendommen. I motsetning til konjunksjon og disjunksjon, som tilfredsstiller kravene til kommutativitet, er ikke matrisemultiplikasjonsfunksjonen slik, og omorganisering av faktorene i denne operasjonen vil endre resultatet, samt eksponentiering.
En annen viktig egenskap som ofte brukes i elektronikk og kretsløp er underordning av par av logiske operasjoner til de Morgans lover.

Disse lovene forbinder par med logiske operasjoner medved hjelp av funksjonen til logisk negasjon, det vil si at de lar deg uttrykke en logisk operasjon ved hjelp av en annen. For eksempel kan negasjonsfunksjonen til en konjunktjon uttrykkes ved hjelp av en disjunksjon av negasjonen av individuelle operander. Ved hjelp av disse lovene kan logiske operasjoner "OG", "ELLER" uttrykkes og implementeres gjensidig med minimale maskinvarekostnader. Denne egenskapen er ekstremt nyttig i kretsløp, da den sparer ressurser når du beregner og former mikrokretsløp.


























