
No mundo de hoje, usamos cada vez maisvários carros e dispositivos. E não apenas quando é necessário usar literalmente a força sobre-humana: mover a carga, elevá-la a uma altura, cavar uma vala longa e profunda, etc. Hoje, os carros são montados por robôs, a comida é preparada por multicooker e cálculos aritméticos elementares são executados por calculadoras. Cada vez mais ouvimos a expressão "álgebra booleana". Talvez tenha chegado a hora de entender o papel do homem na criação de robôs e a capacidade das máquinas de resolver não apenas problemas matemáticos, mas também lógicos.
Traduzido do grego, a lógica éum sistema ordenado de pensamento que cria relações entre condições dadas e permite que inferências sejam feitas com base em premissas e suposições. Muitas vezes nos perguntamos: "É lógico?" A resposta recebida confirma nossas suposições ou critica a linha de pensamento. Mas o processo não para: continuamos a raciocinar.
Às vezes, o número de condições (introdutórias) é tãoé grande, e as interconexões entre eles são tão intrincadas e complexas que o cérebro humano não é capaz de "digerir" tudo de uma vez. Pode demorar mais de um mês (semana, ano) para entender o que está acontecendo. Mas a vida moderna não nos dá esses intervalos de tempo para tomar decisões. E usamos computadores. E é aí que surge a álgebra da lógica, com suas próprias leis e propriedades. Ao baixar todos os dados originais, permitimos que o computador reconheça todas as interconexões, elimine contradições e encontre uma solução satisfatória.

Gottfried Wilhelm Leibniz famosoformulou o conceito de "lógica matemática", cujas tarefas estavam disponíveis para compreensão apenas para um estreito círculo de cientistas. Essa direção não despertou muito interesse e, até meados do século 19, poucos sabiam sobre lógica matemática.
Despertou grande interesse nas comunidades científicasuma disputa em que o inglês George Boole anunciou sua intenção de criar um ramo da matemática que não tem absolutamente nenhuma aplicação prática. Como lembramos da história, nessa época a produção industrial estava se desenvolvendo ativamente, todos os tipos de máquinas auxiliares e máquinas-ferramenta foram desenvolvidas, ou seja, todas as descobertas científicas tinham uma orientação prática.
Olhando para o futuro, dizemos que a álgebra booleana é a parte da matemática mais usada no mundo moderno. Então Boole perdeu seu argumento.
A própria personalidade do autor merece um separadoatenção. Mesmo levando em consideração o fato de que no passado as pessoas cresceram antes de nós, ainda não se pode ignorar que aos 16 anos J. Boole lecionava em uma escola de aldeia e aos 20 abriu sua própria escola em Lincoln. O matemático era fluente em cinco línguas estrangeiras e nas horas vagas lia as obras de Newton e Lagrange. E tudo isso é filho de um simples trabalhador!

Em 1839, Boulle enviou pela primeira vez suatrabalho no Cambridge Mathematical Journal. O cientista tem 24 anos. O trabalho de Boole atraiu o interesse de membros da Royal Scientific Society, que em 1844 ele recebeu uma medalha por sua contribuição para o desenvolvimento da análise matemática. Vários outros trabalhos publicados descrevendo elementos de lógica matemática permitiram ao jovem matemático assumir o cargo de professor no County Cork College. Lembremos que o próprio Buhl não teve educação.
Em princípio, a álgebra booleana é muito simples.Existem afirmações (expressões lógicas) que, do ponto de vista da matemática, podem ser definidas apenas em duas palavras: "verdadeiro" ou "falso". Por exemplo, na primavera as árvores florescem - verdade, no verão neva - uma mentira. A beleza dessa matemática é que não há necessidade estrita de usar apenas números. Quaisquer declarações com um significado inequívoco são bastante adequadas para a álgebra de julgamentos.
Portanto, a álgebra da lógica pode serusado literalmente em qualquer lugar: na programação e redação de instruções, analisando informações conflitantes sobre eventos e determinando a sequência de ações. O mais importante é compreender que não importa em absoluto como determinamos a verdade ou falsidade de uma afirmação. Destes "como" e "por que" é necessário abstrair. Apenas a declaração do fato importa: verdadeiro-falso.
Claro, as funções são importantes para a programaçãoálgebras de lógica, que são escritas com os sinais e símbolos correspondentes. E aprendê-los significa dominar uma nova língua estrangeira. Nada é impossível.
Sem entrar em detalhes, vamos entender a terminologia. Portanto, a álgebra booleana assume a presença de:
Declarações - qualquer expressão afirmativa,que não pode ser interpretado de duas maneiras. Eles são escritos na forma de números (5> 3) ou formulados em palavras familiares (um elefante é o maior mamífero). Além disso, a frase "a girafa não tem pescoço" também tem o direito de existir, apenas a álgebra booleana a definirá como "falsa".
Todas as declarações devem ser inequívocascaráter, mas podem ser elementares e compostos. O último usa conectivos lógicos. Ou seja, na álgebra de julgamentos, as afirmações compostas são formadas pela adição de outras elementares por meio de operações lógicas.

Já lembramos que as operações na álgebra de julgamentos sãoquebra-cabeças. Assim como a álgebra numérica usa operações aritméticas para adicionar, subtrair ou comparar números, os elementos da lógica matemática podem ser usados para formar afirmações complexas, negar ou calcular o resultado final.
Operações lógicas para formalização e simplicidadesão escritos em fórmulas que conhecemos na aritmética. As propriedades da álgebra booleana tornam possível escrever equações e calcular incógnitas. As operações lógicas geralmente são escritas usando uma tabela verdade. Suas colunas definem os elementos dos cálculos e a operação que é realizada sobre eles, e as linhas mostram o resultado dos cálculos.
Mais comum na álgebra booleanaas operações são negação (NOT) e AND e OR lógicos. Quase todas as ações na álgebra de julgamentos podem ser descritas dessa maneira. Vamos estudar cada uma das três operações com mais detalhes.
Negação (não) se aplica a apenas umelemento (operando). Portanto, a operação de negação é chamada de unária. Para escrever o conceito "não A", use os seguintes símbolos: ¬A, A¯¯¯ ou! A. Na forma tabular, é assim:
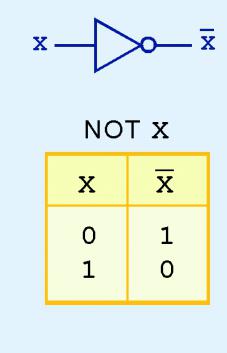
A função de negação é caracterizada pela seguinte afirmação: se A é verdadeiro, então A é falso. Por exemplo, a Lua gira em torno da Terra - verdade; A terra gira em torno da lua - uma mentira.
O AND lógico é chamado de operação de conjunção.O que isso significa? Primeiro, que pode ser aplicado a dois operandos, ou seja, AND é uma operação binária. Segundo, que apenas se ambos os operandos (A e B) forem verdadeiros, a própria expressão é verdadeira. O provérbio “Paciência e trabalho irão moer tudo” sugere que apenas os dois fatores ajudarão uma pessoa a lidar com as dificuldades.
Os seguintes símbolos são usados para escrever: A∧Б, A⋅Б ou A && B.
A conjunção é análoga à multiplicação na aritmética. Às vezes, eles dizem isso - multiplicação lógica. Se multiplicarmos os elementos da tabela por linhas, obteremos o resultado semelhante ao pensamento lógico.
A disjunção é uma operação OR lógica.Ele assume o valor de verdade quando pelo menos uma das afirmações é verdadeira (A ou B). Está escrito assim: A∨B, A + B ou A || B. As tabelas de verdade para essas operações são:
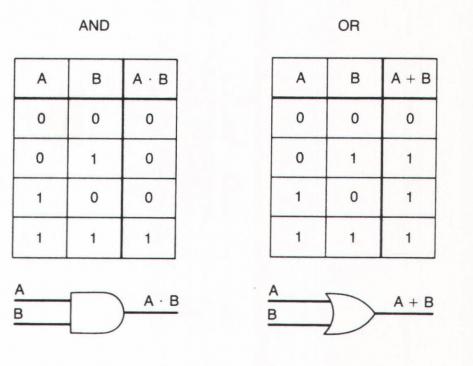
Disjunção é como adição aritmética.A operação de adição lógica tem apenas uma limitação: 1 + 1 = 1. Mas lembramos que no formato digital, a lógica matemática é limitada a 0 e 1 (onde 1 é verdadeiro, 0 é falso). Por exemplo, a declaração “em um museu você pode ver uma obra-prima ou encontrar um interlocutor interessante” significa que você pode ver obras de arte ou pode encontrar uma pessoa interessante. Ao mesmo tempo, não está excluída a opção de ocorrência simultânea de ambos os eventos.
Então, já sabemos quais operações lógicasusa álgebra booleana. As funções descrevem todas as propriedades dos elementos da lógica matemática e permitem que você simplifique as condições de problemas compostos complexos. A propriedade mais compreensível e simples parece ser a propriedade de rejeição de operações derivadas. Derivados significam OR, implicação e equivalência exclusivos. Como nos familiarizamos apenas com as operações básicas, também consideraremos as propriedades apenas delas.
Associatividade significa que em declarações como "A, B e C", a seqüência de enumeração dos operandos não importa. A fórmula será escrita assim:
(A∧B) ∧V = A∧ (B∧V) = A∧B∧V,
(A∨B) ∨V = A∨ (B∨V) = A∨B∨V.
Como você pode ver, isso é característico não apenas da conjunção, mas também da disjunção.

Comutatividade afirma que o resultado da conjunção ou disjunção não depende de qual elemento foi considerado primeiro:
A∧B = B∧A; A∨B = B∨A.
Distributividade permite expandir parênteses em expressões lógicas complexas. As regras são semelhantes à expansão de parênteses para multiplicação e adição em álgebra:
A∧ (B∨V) = A∧Б∨A∧В; A∨Б∧В = (A∨Б) ∧ (A∨В).
Propriedades de um e zero, que pode ser um dos operandos, também são análogos à multiplicação algébrica por zero ou um e adição por um:
A∧0 = 0, A∧1 = A; A∨0 = A, A∨1 = 1.
Idempotência nos diz que, se em relação a doisde operandos iguais, o resultado da operação acaba sendo o mesmo, então você pode "descartar" operandos desnecessários, complicando o curso do raciocínio. Tanto a conjunção quanto a disjunção são operações idempotentes.
B∧B = B; B∨B = B.
Absorção também nos permite simplificar as equações.Engolir afirma que, quando outra operação no mesmo elemento é aplicada a uma expressão com um operando, o resultado é o operando da operação de engolir.
A∧Б∨Б = B; (A∨B) ∧B = B.
A sequência de operações tem um importantevalor. Na verdade, como para a álgebra, há uma prioridade das funções usadas pela álgebra booleana. As fórmulas podem ser simplificadas apenas se o significado das operações for observado. Classificando do mais significativo ao insignificante, obtemos a seguinte sequência:
1. Negação.
2. Conjunção.
3. Disjunção, OU exclusivo.
4. Implicação, equivalência.
Como você pode ver, apenas negação e conjunção não têm prioridades iguais. E a prioridade de disjunção e OU exclusivo são iguais, assim como as prioridades de implicação e equivalência.
Como dissemos, além das operações lógicas básicas, a lógica matemática e a teoria dos algoritmos usam derivadas. Os mais comumente usados são implicação e equivalência.
Implicação, ou seguimento lógico, éuma afirmação em que uma ação é uma condição e a outra é uma consequência de seu desempenho. Em outras palavras, esta é uma frase com a preposição "se ... então". "Você gosta de andar, adora carregar trenós." Ou seja, para esquiar, você precisa apertar o trenó morro acima. Se não houver desejo de descer a montanha, não há necessidade de carregar um trenó. Está escrito assim: A → B ou A⇒B.
A equivalência assume que o resultadoa ação ocorre apenas quando ambos os operandos são verdadeiros. Por exemplo, a noite dá lugar ao dia quando (e só então) quando o sol nasce no horizonte. Na linguagem da lógica matemática, esta declaração é escrita da seguinte forma: A≡B, A⇔B, A == B.
A álgebra de julgamentos está se desenvolvendo, e muitoscientistas interessados formularam novas leis. Os mais famosos são os postulados do matemático escocês O. de Morgan. Ele percebeu e definiu propriedades como negação próxima, complemento e negação dupla.
Fechar negação assume que não há negação antes do parêntese: não (A ou B) = não A ou NÃO B.
Quando o operando é negado, independentemente de seu valor, fala-se de Adição:
B∧¬B = 0; B∨¬B = 1.
E finalmente duas vezes não compensa por si mesmo. Essa. antes do operando, ou a negação desaparece ou apenas uma permanece.
A lógica matemática implica simplificaçãodadas equações. Assim como na álgebra, você deve primeiro atenuar a condição tanto quanto possível (livrar-se de entradas e operações complexas com elas) e, em seguida, começar a procurar pela resposta correta.
O que pode ser feito para simplificar?Converta todas as operações derivadas em operações simples. Em seguida, expanda todos os parênteses (ou vice-versa, coloque-os fora dos parênteses para encurtar este elemento). O próximo passo é aplicar as propriedades da álgebra booleana na prática (absorção, propriedades de zero e um, etc.).

Em última análise, a equação deve consistir emo número mínimo de incógnitas combinadas por operações simples. A maneira mais fácil de encontrar uma solução é quando você obtém muitos negativos próximos. Então a resposta aparecerá como se fosse por si mesma.


























