
La începutul secolului al XIX-lea, geometrul berlinez Jakob Steinera stabilit sarcina de a lega trei sate, astfel încât lungimea lor să fie cea mai scurtă. Ulterior, el a generalizat această problemă: este necesar să se găsească un punct pe plan astfel încât distanța de la el la alte n puncte să fie cea mai mică. În secolul al XX-lea, lucrările pe această temă au continuat. S-a decis să se ia mai multe puncte și să le conecteze în așa fel încât distanța dintre ele să fie cea mai mică. Acesta este tot un caz special al problemei studiate.
Algoritmul lui Kruskal aparține algoritmilor „lacomi”.(se mai numesc și gradient). Esența acestora este cel mai mare câștig la fiecare pas. Nu întotdeauna algoritmii „lacomi” oferă cea mai bună soluție la problemă. Există o teorie care arată că atunci când sunt aplicate la anumite probleme, ele oferă soluția optimă. Aceasta este teoria matroidei. Algoritmul Kruskal aparține unor astfel de probleme.
Algoritmul considerat construiește optimulcadru grafic. Sarcina sa este următoarea. Având în vedere un grafic nedirecționat fără mai multe muchii și bucle, și pe mulțimea muchiilor sale, este dată o funcție de greutate w, care atribuie fiecărei muchii e un număr - greutatea muchiei - w(e). Greutatea fiecărui submult al setului de muchii este determinată de suma greutăților muchiilor sale. Este necesar să găsiți cadrul cu cea mai mică greutate.
Algoritmul lui Kruskal funcționează așa.În primul rând, toate marginile graficului original sunt aranjate în ordinea crescătoare a greutăților. Inițial, cadrul nu conține nicio muchie, dar include toate vârfurile graficului. După următorul pas al algoritmului, o margine este adăugată părții deja construite a cadrului, care este pădurea care se întinde. Nu este ales arbitrar. Toate marginile graficului care nu aparțin cadrului pot fi numite roșii și verzi. Vârfurile fiecărei margini roșii se află în aceeași componentă conexă a pădurii în construcție, iar vârfurile celei verzi se află în altele diferite. Prin urmare, dacă acolo se adaugă o margine roșie, apare un ciclu, iar dacă se adaugă o margine verde, componenta de conexiune în pădure obținută după acest pas va fi cu una mai mică. Astfel, nu poate fi adăugată nicio margine roșie la construcția rezultată, dar orice margine verde poate fi adăugată pentru a obține o pădure. Și se adaugă o margine verde cu o greutate minimă. Rezultatul este un cadru de cea mai mică greutate.
Să notăm pădurea actuală cu F.Împarte setul de vârfuri ale grafului în regiuni conectate (uniunea lor formează F și sunt disjunse pe perechi). Pentru marginile roșii, ambele vârfuri se află în aceeași parte. Part(x) este o funcție care, pentru fiecare vârf x, returnează numele părții căreia îi aparține x. Unite(x,y) este o procedură care construiește o nouă partiție constând din unirea părților x și y și a tuturor celorlalte părți. Fie n numărul muchiilor graficului. Toate aceste concepte sunt incluse în algoritmul lui Kruskal. Implementare:
Sortați toate marginile graficului de la 1 la a n-a în ordine crescătoare a greutăților. (ai, bi sunt vârfuri ale muchiei cu numărul i).
pentru i = 1 la n do.
x := Part(ai).
y := Partea(bi).
Dacă x nu este egal cu y, atunci Uniți (x, y), includeți muchia i în F.
Fie T cadrul graficului original construit folosind algoritmul Kruskal și S cadrul său arbitrar. Trebuie să demonstrăm că w(T) nu depășește w(S).
Fie M mulțimea muchiilor S, P mulțimea muchiilorT. Dacă S nu este egal cu T, atunci există o muchie et a cadrului T care nu aparține lui S. Atașați et la S. Se formează un ciclu, să-l numim C. Îndepărtați din C orice muchie aparținând lui S. Primim un nou cadru, pentru că marginile și sunt atât de multe vârfuri în el. Greutatea sa nu depășește w(S), deoarece w(et) este cel mult w(es) datorită algoritmului lui Kruskal. Vom repeta această operație (înlocuind muchiile lui S cu muchiile lui T) până când obținem T. Greutatea fiecărui cadru ulterior obținut nu este mai mare decât greutatea celui precedent, ceea ce implică faptul că w(T) nu este mai mare. decât w(S).
De asemenea, corectitudinea algoritmului lui Kruskal rezultă din teorema matroidei Rado-Edmonds.
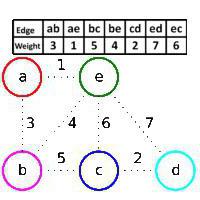
Dat un grafic cu vârfuri a, b, c, d, e și muchii (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Greutățile coastelor sunt prezentate în tabel și în figură. În primul rând, pădurea construită F conține toate vârfurile graficului și nu conține muchii. Algoritmul lui Kruskal va adăuga mai întâi muchia (a, e), deoarece are cea mai mică greutate, iar vârfurile a și e sunt în diferite componente conectate ale pădurii F (muchia (a, e) este verde), apoi muchia (c , d), astfel încât această muchie să aibă cea mai mică pondere dintre muchiile graficului care nu sunt în F și să fie verde, atunci muchia (a, b) se adaugă din aceleași motive. Dar muchia (b, e) se omite, deși are cea mai mică pondere dintre muchiile rămase, pentru că este roșie: vârfurile b și e aparțin aceleiași componente conexe a pădurii F, adică dacă adăugăm marginea (b, e) la F, obținem ciclu. Apoi se adaugă marginea verde (b, c), se omite marginea roșie (c, e) și apoi d, e. Astfel, muchiile (a, e), (c, d), (a, b), (b, c) sunt adăugate secvenţial. Cadrul optim al graficului original nu constă din nimic. Așa funcționează algoritmul în acest caz. Kraskala. Un exemplu a arătat acest lucru.

Figura prezintă un grafic format din două componente conectate. Liniile aldine arată marginile cadrului optim (verde) construit folosind algoritmul Kruskal.

Figura de sus arată graficul original, iar cea de jos arată cadrul de greutate minimă construit pentru acesta folosind algoritmul considerat.
Secvența muchiilor adăugate: (1,6); (0,3), (2,6) sau (2,6), (0,3) - nu contează; (3,4); (0.1), (1.6) sau (1.6), (0.1), de asemenea, nu contează (5.6).

Algoritmul Kraskal își găsește aplicație practică, de exemplu, pentru optimizarea amenajării comunicațiilor, drumurilor în noi microdistricte ale așezărilor din fiecare țară, precum și în alte cazuri.


























