
Сейчас речь пойдет о геометрической оптике.În această secțiune, este dedicat mult timp unui astfel de obiect precum o lentilă. La urma urmei, poate fi altfel. În același timp, formula unui obiectiv subțire este aceeași pentru toate cazurile. Trebuie doar să știi cum să o aplici corect.

Este întotdeauna un corp transparent la razele luminoase, care are o formă specială. Aspectul obiectului este dictat de două suprafețe sferice. Unul dintre ele poate fi înlocuit cu unul plat.
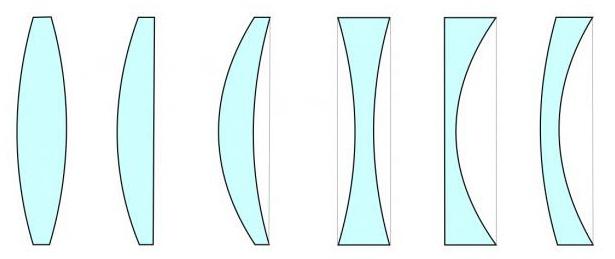
Причем у линзы может оказаться толще середина или marginile. În primul caz, se va numi convex, în al doilea - concave. Mai mult, în funcție de cum sunt combinate suprafețele concave, convexe și plane, lentilele pot fi de asemenea diferite. Anume: biconvexe și biconcave, plano-convexe și plano-concave, convexe-concave și concave-convexe.
В обычных условиях эти объекты используются в în văzduh. Sunt fabricate dintr-o substanță a cărei densitate optică este mai mare decât cea a aerului. Prin urmare, o lentilă convexă se va colecta, iar o lentilă concavă va fi împrăștiată.
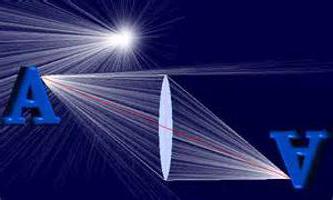
Înainte de a vorbi despre formulă subțire a lentilelor, trebuie să decideți conceptele de bază. Ele trebuie cunoscute. Întrucât vor fi abordate în mod constant prin diferite sarcini.
Главная оптическая ось — это прямая.Este desenat prin centrele ambelor suprafețe sferice și determină locația centrului lentilei. Există axe optice suplimentare. Ele sunt trase printr-un punct care este centrul lentilei, dar nu conțin centrele suprafețelor sferice.
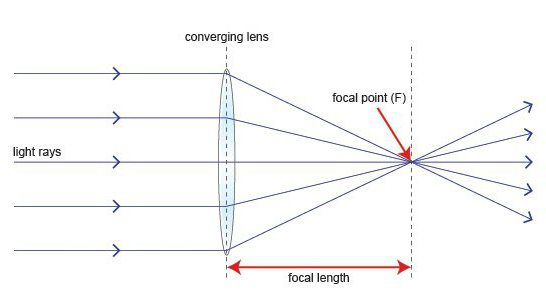
În formula unei lentile subțiri există o cantitate care îi determină distanța focală. Deci, accentul este un punct pe axa optică principală. În ea se intersectează razele care trec paralel cu axa specificată.
Mai mult, există întotdeauna două trucuri pentru fiecare lentilă subțire. Sunt localizate pe ambele părți ale suprafețelor sale. Ambele focus pe colecționar sunt valabile. În împrăștiere - imaginar.
Distanța de la obiectiv la punctul focal este distanța focală (literă F). Mai mult, valoarea sa poate fi pozitivă (în cazul colectării) sau negativă (pentru împrăștiere).
O altă caracteristică este asociată cu distanța focală - puterea optică. Este obișnuit să denotăm D. Valoarea sa este întotdeauna reciproca focalizării, adică. D = 1 /F. Puterea optică măsurată la dioptrii (dioptrii prescurtate).
Pe lângă distanța focală deja specificată, va trebui să cunoașteți mai multe distanțe și dimensiuni. Pentru toate tipurile de lentile sunt aceleași și sunt prezentate în tabel.
| denumire | nume |
| d | distanța față de subiect |
| x | înălțimea subiectului studiat |
| f | distanța față de imagine |
| X | înălțimea imaginii rezultate |
Toate distanțele și înălțimile indicate sunt de obicei măsurate în metri.
În fizică, noțiunea de mărire este asociată și cu formula unui obiectiv subțire. Este definit ca raportul dintre dimensiunea imaginii și înălțimea subiectului, adică H / h. Poate fi notat prin litera G.
Trebuie să știți acest lucru pentru a obține formulalentilă subțire, colectare sau împrăștiere. Desenul începe cu faptul că ambele lentile au propria lor imagine schematică. Ambele arată ca o tăietură. Numai în colectarea de la capetele sale săgețile sunt îndreptate spre exterior, iar în împrăștiere - în interiorul acestui segment.
Acum este necesar să se atragă către acest segmentperpendicular pe mijlocul său. Aceasta va arăta axa optică principală. Pe ea, pe ambele părți ale lentilei la aceeași distanță, se presupune că notează trucuri.
Obiectul a cărui imagine doriți să o construiți este desenat sub forma unei săgeți. Acesta arată unde se află partea de sus a articolului. În general, un obiect este plasat paralel cu lentila.
Pentru a construi o imagine a unui obiect,găsiți doar punctele capetelor imaginii și apoi conectați-le. Fiecare dintre aceste două puncte poate rezulta din intersecția a două raze. Cele mai simple de construit sunt două dintre ele.
Venind din punctul specificat paralel cu principalulaxa optică. După contactul cu lentila, el trece prin focalizarea principală. Dacă vorbim despre o lentilă colectoare, atunci această focalizare se află în spatele lentilei și fasciculul trece prin ea. Când se are în vedere împrăștierea, fasciculul trebuie desenat astfel încât continuarea lui să treacă prin focalizarea din fața obiectivului.
Trecând direct prin centrul optic al obiectivului. El nu-și schimbă direcția după ea.
Există situații când un articol este livratperpendicular pe axa optică principală și se termină pe ea. Apoi, este suficient să construiți o imagine a unui punct care să corespundă cu marginea săgeții, care nu se află pe axa. Și apoi trageți din ea o perpendiculară pe axă. Aceasta va fi imaginea subiectului.
Intersecția punctelor construite dă o imagine.Într-o lentilă subțire de colectare, se obține o imagine reală. Adică se obține direct la intersecția razelor. O excepție este situația când subiectul este plasat între obiectiv și focalizare (ca într-o lupă), apoi imaginea se dovedește a fi imaginară. În împrăștiere, se dovedește întotdeauna imaginar. La urma urmei, se obține la intersecția nu a razelor în sine, ci a extensiilor acestora.
Imaginea reală este de obicei desenată cu o linie solidă. Dar imaginarul - linie punctată. Acest lucru se datorează faptului că primul este de fapt prezent acolo, iar al doilea este văzut doar.
Acest lucru este realizat în mod convenabil pe baza unui desen care ilustrează construcția unei imagini reale într-un obiectiv de colectare. Desemnarea segmentelor este indicată pe desen.
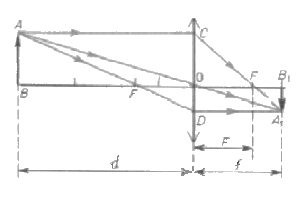
Secțiunea optică nu se numește degeaba geometrică. Va lua cunoștințe din această secțiune de matematică. Mai întâi trebuie să luați în considerare triunghiurile AOW și A1OB1. Sunt similare, deoarece au două unghiuri egale (drept și vertical). Din similitudinea lor rezultă că modulele segmentelor A1În1 și AB se referă ca module ale segmentelor OB1 și OB.
Similare (bazate pe același principiu în două unghiuri) sunt încă două triunghiuri: COF și A1SE1. În ele, relațiile unor astfel de module de segmente sunt egale: A1În1 cu CO și SE1cu DE. Pe baza construcției, segmentele AB și CO vor fi egale. Prin urmare, partea stângă a egalităților de relații indicate este aceeași. Prin urmare, drepturile sunt egale. Adică OB1 / S este egal SE1/ DE.
În egalitatea indicată, segmentele indicate prin puncte pot fi înlocuite cu conceptele fizice corespunzătoare. Deci ov1 Este distanța de la obiectiv la imagine. OB este distanța de la subiect la obiectiv. DE - distanta focala. Un segment SE1 este egal cu diferența dintre distanța față de imagine și focalizare. Prin urmare, poate fi rescris într-un mod diferit:
f / d = (f - F) / F sau Ff = df - dF.
Pentru a obține formula pentru o lentilă subțire, ultima egalitate trebuie împărțită la dfF. Apoi se dovedește:
1 / d + 1 / f = 1 / F.
Are formula unei lentile colectoare subțiri.Distanța focală divergentă este negativă. Acest lucru duce la o schimbare a egalității. Adevărat, este nesemnificativ. Doar că în formula unei lentile difuze subțiri există un minus înainte de raportul 1 /F. Adică:
1 / d + 1 / f = - 1 / F.
Condiție. Distanța focală a obiectivului colector este de 0,26 m. Este necesar să se calculeze mărirea acestuia dacă obiectul se află la o distanță de 30 cm.
Decizie. Ar trebui să înceapă cu introducerea desemnărilor și conversia unităților în C. Deci, cunoscut d = 30 cm = 0,3 m și F = 0,26 m. Acum trebuie să alegeți formulele, cea principală este cea indicată pentru mărire, a doua este pentru o lentilă subțire de colectare.
Trebuie combinate cumva. Pentru a face acest lucru, va trebui să luați în considerare un desen pentru construirea unei imagini într-un obiectiv de colectare. Se poate vedea din astfel de triunghiuri că Г = H / h= f / d. Adică, pentru a găsi mărirea, va trebui să calculați raportul dintre distanța față de imagine și distanța față de obiect.
Al doilea este cunoscut. Dar distanța față de imagine ar trebui să fie derivată din formula indicată anterior. Se pare că
f = dF / (d - F).
Acum aceste două formule trebuie combinate.
Г = dF / (d(d - F)) = F / (d - F).
În acest moment, soluția problemei pentru formula pentru o lentilă subțire este redusă la calcule elementare. Rămâne să înlocuiți valorile cunoscute:
G = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Răspuns: obiectivul oferă o mărire de 6,5 ori.

Condiție. Lampa este situată la un metru de obiectivul colector. Imaginea spiralei sale este obținută pe un ecran situat la 25 cm distanță de obiectiv.Calculați distanța focală a obiectivului specificat.
Decizie. Se presupune că va scrie următoarele date în date: d = 1 m și f = 25 cm = 0,25 m. Aceste informații sunt suficiente pentru a calcula distanța focală din formula pentru un obiectiv subțire.
Deci 1 /F = 1/1 + 1 / 0,25 = 1 + 4 = 5. Dar sarcina necesită cunoașterea focalizării, nu puterea optică. Prin urmare, rămâne doar să împărțiți 1 la 5 și obțineți distanța focală:
F = 1/5 = 0,2 m.
Răspuns: Distanța focală a obiectivului colector este de 0,2 m.
Condiție... Lumânarea a fost plasată la o distanță de 15 cm de lentila colectoare. Puterea sa optică este de 10 dioptrii. Ecranul din spatele obiectivului este poziționat astfel încât să se obțină o imagine clară a lumânării. Cu ce este egală această distanță?
Decizie. Se presupune că scrie următoarele date într-o scurtă înregistrare: d = 15 cm = 0,15 m, D = 10 dioptrii. Formula prezentată mai sus trebuie scrisă cu o ușoară modificare. Și anume, pe partea dreaptă a egalității, puneți D în loc de 1 /F.
După mai multe transformări, se obține următoarea formulă pentru distanța de la obiectiv la imagine:
f = d / (dD - unu).
Acum trebuie să înlocuiți toate numerele și să numărați. Se dovedește o astfel de valoare pentru f: 0,3 m.
Răspuns: Distanța de la obiectiv la ecran este de 0,3 m.

Condiție. Obiectul și imaginea sa sunt separate una de cealaltă cu 11 cm. Obiectivul colector dă o mărire de 3 ori. Găsiți distanța focală.
Decizie. Distanța dintre obiect și imaginea sa este indicată în mod convenabil printr-o scrisoare L = 72 cm = 0,72 m. Mărire G = 3.
Două situații sunt posibile aici.Primul este că subiectul se află în spatele focalizării, adică imaginea este reală. În al doilea, există un obiect între focalizare și obiectiv. Apoi imaginea este din aceeași parte cu obiectul și este imaginară.
Să luăm în considerare prima situație. Obiectul și imaginea se află pe părțile opuse ale obiectivului colector. Aici puteți scrie următoarea formulă: L = d + f. A doua ecuație ar trebui să fie scrisă: Г = f / d. Este necesar să se rezolve sistemul acestor ecuații cu două necunoscute. Pentru a face acest lucru, înlocuiți L cu 0,72 m, iar G cu 3.
Din a doua ecuație rezultă că f = 3d. Apoi primul se transformă astfel: 0,72 = 4d. Este ușor de numărat din ea d = 0,18 (m). Acum este ușor de definit f = 0,54 (m).
Rămâne să folosiți formula lentilelor subțiri pentru a calcula distanța focală. F = (0,18 * 0,54) / (0,18 + 0,54) = 0,135 (m). Acesta este răspunsul pentru primul caz.
În a doua situație, imaginea este imaginară, iar formula pentru L va fi diferit: L = f - d. A doua ecuație pentru sistem va fi aceeași. Argumentând în mod similar, constatăm că d = 0,36 (m) și f = 1,08 (m). Un calcul similar al distanței focale va da următorul rezultat: 0,54 (m).
Răspuns: Distanța focală a obiectivului este de 0,135 m sau 0,54 m.
Calea razelor într-o lentilă subțire este importantăaplicarea practică a opticii geometrice. La urma urmei, acestea sunt utilizate în multe dispozitive, de la simple lupe la microscopuri și telescoape de precizie. Prin urmare, este necesar să știm despre ele.
Formula derivată a unei lentile subțiri face posibilă rezolvareamulte sarcini. Mai mult, vă permite să trageți concluzii despre ce imagine oferă diferite tipuri de lentile. În acest caz, este suficient să îi cunoaștem distanța focală și distanța față de obiect.


























