
História pythagorejskej vety má niekoľkotisícročia. Tvrdenie, že štvorec prepony sa rovná súčtu štvorcov nôh, bola známa dávno pred narodením gréckeho matematika. Pythagorova veta, história stvorenia a jej dôkaz sú však pre väčšinu vedcov spojené s týmto vedcom. Podľa niektorých prameňov to bol prvý dôkaz vety, ktorý dal Pythagoras. Niektorí vedci však túto skutočnosť vyvracajú.

Predtým, ako ti poviem, ako sa príbeh formovalVeta z Pythagora, stručne sa zaoberáme biografiou matematika. Žil v 6. storočí pred naším letopočtom. Dátum narodenia Pythagoras sa považuje za 570 rokov pred Kristom. e., miesto - ostrov Samos. O živote vedca je málo známe. Biografické údaje v starogréckych prameňoch sú previazané s čistou fikciou. Na stránkach pojednaní sa javí ako veľký mudrc, vynikajúco ovládajúce slová a schopnosť presvedčiť. Mimochodom, z tohto dôvodu sa grécky matematik nazýval Pythagoras, to znamená „presvedčivá reč“. Podľa inej verzie, Pythia predpovedal vznik budúceho mudrca. Otec menoval chlapca Pythagorasom na svoju česť.

Mudrc sa poučil z veľkých myslí dňa.Medzi učiteľmi mladých Pythagorov sú Hermodamantus a Therekides of Syros. Prvý v ňom vštepil lásku k hudbe, druhý ho naučil filozofii. Obidve tieto vedy budú počas celého života ostať stredobodom pozornosti vedcov.
Podľa jednej verzie je zvedavý mladý muž,Pythagoras opustil svoju vlasť. Šiel hľadať vedomosti v Egypte, kde podľa rôznych zdrojov zostal od 11 do 22 rokov, potom bol zajatý a poslaný do Babylona. Pythagoras mal z jeho postavenia úžitok. 12 rokov študoval matematiku, geometriu a mágiu v starovekom štáte. Pythagoras sa k Samosovi vrátil až vo veku 56 rokov. V tom čase vládol tyranský polycrát. Pythagoras nemohol akceptovať takýto politický systém a čoskoro išiel na juh Talianska, kde sa nachádzala grécka kolónia Croton.
Dnes nie je možné s istotou povedať, či sa Pythagoras nachádzal v Egypte a Babylone. Možno odišiel Samos neskôr a išiel priamo do Crotonu.

S vývojom súvisí aj história pytagorejskej vetyškola vytvorená gréckym filozofom. Toto náboženské a etické bratstvo kázalo dodržiavanie osobitného spôsobu života, študovalo aritmetiku, geometriu a astronómiu a študovalo filozofickú a mystickú stránku čísel.
Все открытия учеников греческого математика prisúdil mu. Dejiny vzniku pythagorejskej vety však spájajú starí životopisci iba so samotným filozofom. Predpokladá sa, že Grékom odovzdal vedomosti, ktoré získal v Babylone a Egypte. Existuje aj verzia, ktorú skutočne objavil vetu o pomeroch nôh a prepony, nevediac o úspechoch iných národov.
V niektorých starogréckych prameňochpopisuje radosť Pytagorova, keď sa mu podarilo dokázať vetu. Na počesť takejto udalosti nariadil obetovať bohom v podobe stoviek býkov a urobil hostinu. Niektorí vedci však poukazujú na nemožnosť takéhoto činu kvôli zvláštnostiam názorov Pytagorejcov.
Predpokladá sa, že v pojednaní "Začiatky", vytvorilEuclid, autor podáva dôkaz o vete, ktorej autorom bol veľký grécky matematik. Nie všetci však tento názor podporili. Napríklad staroveký neopoplatonistický filozof Proclus poukázal na to, že autorom dôkazu poskytnutého v Prvkoch je sám Euklid.
Nech je to už akokoľvek, ale Pythagoras nebol prvý, kto formuloval vetu.

Pytagorova veta, ktorej história vzniklapovažovaný v článku, podľa nemeckého matematika Cantora, bol známy už v roku 2300 pred naším letopočtom. e. v Egypte. Starí obyvatelia údolia Nílu za vlády faraóna Amenemhata som poznal rovnosť 32 + 4² = 5²... Predpokladá sa, že pomocou trojuholníkov so stranami 3, 4 a 5 sa egyptské „ťahy lanom“ zoradia do pravých uhlov.
Poznali vetu o Pytagorasovi v Babylone.Hlinené tablety pochádzajúce z roku 2000 pred naším letopočtom a pripísaná vláde kráľa Hammurabího, sa našiel približný výpočet prepony pravouhlého trojuholníka.
História Pytagorovej vety je spojená so starýmicivilizácie Indie a Číny. Pojednanie „Zhou-bi Xuan Jin“ obsahuje náznaky, že egyptský trojuholník (jeho strany sú vo vzájomnom vzťahu 3: 4: 5) bol v Číne známy už v 12. storočí. Pred Kr e. a do VI. storočia. Pred Kr e. matematici tohto štátu poznali všeobecnú podobu vety.
Konštrukciu pravého uhla pomocou egyptského trojuholníka popísalo aj indické pojednanie „Sulva Sutra“, ktoré sa datuje do 7. - 5. storočia. Pred Kr e.
Takže história Pytagorovej vety v čase narodenia gréckeho matematika a filozofa bola už niekoľko sto rokov stará.
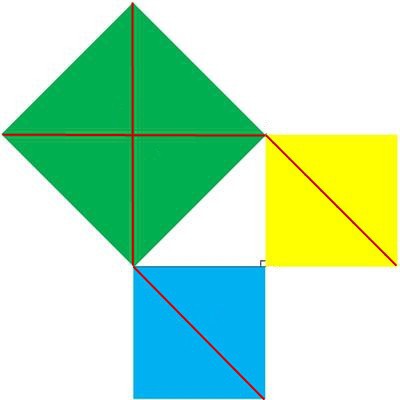
Počas svojej existencie sa teorém stal jednýmzákladných v geometrii. História dôkazu Pytagorovej vety sa pravdepodobne začala zvažovaním rovnostranného pravouhlého trojuholníka. Na jej prepone a nohách sú postavené štvorce. Ten, ktorý „vyrástol“ na preponu, bude pozostávať zo štyroch trojuholníkov, ktoré sa rovnajú prvému. V tomto prípade sa štvorce na nohách skladajú z dvoch takýchto trojuholníkov. Jednoduché grafické znázornenie jasne ukazuje platnosť výroku formulovaného v podobe slávnej vety.
Kombinuje sa ďalší jednoduchý dôkazgeometria s algebrou. Štyri rovnaké pravouhlé trojuholníky so stranami a, b, c sú nakreslené tak, že tvoria dva štvorce: vonkajší so stranou (a + b) a vnútorný so stranou c. V takom prípade sa plocha menšieho štvorca bude rovnať2... Plocha veľkého sa počíta zo súčtu plôch malého štvorca a všetkých trojuholníkov (plocha pravouhlého trojuholníka, vyvolanie, sa počíta podľa vzorca (a * b) / 2), teda s2 + 4 * ((a * b) / 2), čo sa rovná c2 + 2av. Plochu veľkého štvorca je možné vypočítať iným spôsobom - ako produkt dvoch strán, to znamená (a + b)2, ktorá sa rovná a2 + 2av + b2... Ukázalo sa:
a2 + 2av + b2 = s2 + 2av,
a2 + v2 = s2.
Existuje mnoho spôsobov, ako to dokázaťvety. Pracovali na nich aj Euclid, indickí vedci a Leonardo da Vinci. Starovekí mudrci často uvádzali kresby, ktorých príklady sú umiestnené vyššie, a okrem poznámky „Pozri sa!“ Ich nesprevádzali žiadnym vysvetlením. Jednoduchosť geometrického dôkazu, s výhradou určitých znalostí, si nevyžadovala komentáre.
História Pytagorovej vety, zhrnutá v rokutento článok odhaľuje mýtus o jeho pôvode. Je však ťažké si vôbec predstaviť, že by meno veľkej gréckej matematičky a filozofky s ňou niekedy prestalo byť spájané.


























