
Teraz sa zameriame na geometrickú optiku.V tejto časti sa veľa času venuje objektom, ako sú šošovky. Môže to byť predsa iné. V takom prípade je vzorec pre tenkú šošovku rovnaký pre všetky prípady. Musíte len vedieť, ako ho správne aplikovať.

Vždy ide o telo priehľadné pre lúče svetla, ktoré má zvláštny tvar. Vzhľad objektu je diktovaný dvoma sférickými povrchmi. Jeden z nich je možné nahradiť plochým.
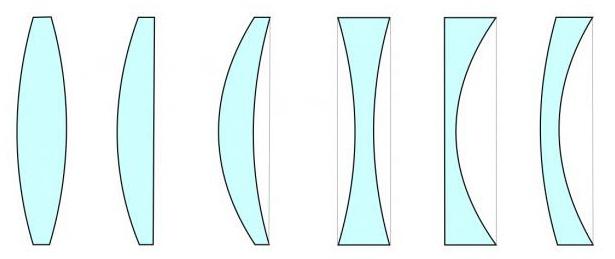
Okrem toho môže byť šošovka v strede silnejšia alebookraje. V prvom prípade sa bude nazývať konvexný, v druhom - konkávny. Okrem toho sa šošovky môžu líšiť v závislosti od toho, ako sú kombinované konkávne, konvexné a ploché povrchy. Menovite: bikonvexné a bikonkávne, plano-konvexné a plano-konkávne, konvexné-konkávne a konkávne-konvexné.
Za normálnych podmienok sa tieto objekty používajú vvzduch. Sú vyrobené z látky, ktorej optická hustota je vyššia ako optická hustota vzduchu. Preto sa bude zhromažďovať konvexná šošovka a konkávna šošovka sa bude rozptyľovať.
Predtým, ako hovoríme o vzorec tenkej šošovky, musíte definovať základné pojmy. Určite ich musíte poznať. Pretože ich budú neustále oslovovať rôzne úlohy.
Hlavná optická os je priamka.Je nakreslený cez stredy oboch sférických povrchov a definuje, kde je stred šošovky. Existujú aj ďalšie optické osi. Sú nakreslené stredovým bodom šošovky, ale neobsahujú stredy sférických povrchov.
Vo vzorci pre tenký objektív existuje hodnota, ktorá určuje jeho ohniskovú vzdialenosť. Takže zameranie je bod na hlavnej optickej osi. Pretína lúče prebiehajúce rovnobežne so zadanou osou.
Pre každý tenký objektív navyše existujú vždy dva triky. Sú umiestnené na oboch stranách jeho povrchov. Obidve zamerania sú platné. Ten rozptýlený je imaginárny.
Vzdialenosť od objektívu k ohnisku je ohnisková vzdialenosť (písmeno F). Jeho hodnota môže byť navyše kladná (v prípade zhromažďovania) alebo záporná (pre rozptyl).
S ohniskovou vzdialenosťou je spojená ďalšia charakteristika - optická sila. Je zvykom to označovať D. Jeho hodnota je vždy inverzná od zamerania, to znamená D = 1 /F. Optický výkon sa meria v dioptriách (skrátene dioptrie).
Okrem už naznačenej ohniskovej vzdialenosti budete musieť poznať niekoľko vzdialeností a veľkostí. Sú rovnaké pre všetky typy šošoviek a sú uvedené v tabuľke.
| označenie | názov |
| d | vzdialenosť k objektu |
| X | výška študovaného predmetu |
| F | vzdialenosť obrazu |
| X | výška výsledného obrázka |
Všetky uvedené vzdialenosti a výšky sa zvyčajne merajú v metroch.
Vo fyzike je koncept zväčšenia spojený aj so vzorcom tenkej šošovky. Je definovaná ako pomer rozmerov obrazu k výške objektu, to znamená H / h. Môže byť označený písmenom G.
Musíte to vedieť, aby ste dostali vzorectenká šošovka, ktorá sa zhromažďuje alebo rozptyľuje. Kresba začína skutočnosťou, že obidve šošovky majú svoje vlastné schematické znázornenie. Oba vyzerajú ako úsečka. Iba pre ten, ktorý sa zhromažďuje na svojich koncoch, sú šípky smerované von a pre rozptyl - vo vnútri tohto segmentu.
Teraz je potrebné ťahať k tomuto segmentukolmo na jeho stred. To bude predstavovať hlavnú optickú os. Na ňom na oboch stranách objektívu v rovnakej vzdialenosti má označovať zaostrenia.
Objekt, ktorý chcete postaviť, je nakreslený vo forme šípky. Ukazuje vám, kde je horná časť položky. Všeobecne je objekt umiestnený rovnobežne s objektívom.
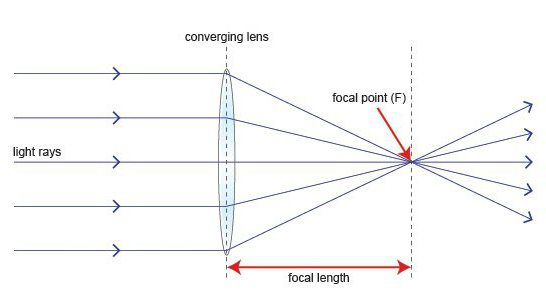
S cieľom vytvoriť obraz objektu,stačí vyhľadať body koncov obrazu a potom ich spojiť. Každý z týchto dvoch bodov možno získať z priesečníka dvoch lúčov. Najľahšie sa budujú dve z nich.
Beží od určeného bodu rovnobežne s hlavnýmoptická os. Po kontakte s objektívom prejde hlavným ohniskom. Ak hovoríme o zbernej šošovke, potom je toto zaostrenie umiestnené za šošovkou a lúč ňou prechádza. Keď sa uvažuje s rozptylovým lúčom, musí byť lúč nasmerovaný tak, aby jeho pokračovanie prešlo ohniskom pred šošovkou.
Ide priamo cez optické zaostrovanie objektívu. Svoj smer po nej nemení.
Existujú situácie, keď je položka dodanákolmo na hlavnú optickú os a končí na nej. Potom stačí zostrojiť obraz bodu, ktorý zodpovedá okraju šípky, ktorý neleží na osi. A potom z nej nakreslite kolmicu na os. Toto bude obrázok objektu.
Priesečník vykreslených bodov dáva obraz.Skutočný obraz sa získa v tenkom konvergujúcom objektíve. To znamená, že sa získava priamo na priesečníku lúčov. Výnimkou je situácia, keď je predmet umiestnený medzi objektívom a ohniskom (ako v lupe), potom sa obraz ukáže ako imaginárny. U rozhádzaného sa vždy ukáže, že je imaginárny. Koniec koncov, to nie je získané na priesečníku samotných lúčov, ale ich rozšírení.
Je obvyklé nakresliť skutočný obrázok plnou čiarou. Ale imaginárne je bodkovaná čiara. Je to spôsobené tým, že prvý tam skutočne je a druhý je iba viditeľný.
Je vhodné to urobiť na základe výkresu ilustrujúceho stavbu skutočného obrazu v zbernej šošovke. Označenie segmentov je uvedené na výkrese.
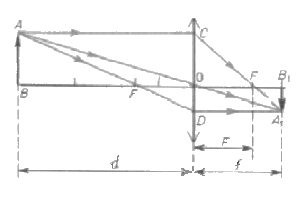
Optická časť sa z nejakého dôvodu nazýva geometrická. Budete potrebovať znalosti z tejto konkrétnej sekcie matematiky. Najprv musíte zvážiť trojuholníky AOB a A1OV1... Sú podobné, pretože majú dva rovnaké uhly (rovný a zvislý). Z ich podobnosti vyplýva, že moduly segmentov A1V1 a AB označujú ako moduly segmentov OB1 a OV.
Dva ďalšie trojuholníky sú podobné (založené na rovnakom princípe v dvoch uhloch): COF a A.1FB1... V nich sú pomery takýchto modulov segmentov rovnaké: А1V1 s CO a FB1s OF. Na základe konštrukcie budú segmenty AB a CO rovnaké. Ľavé strany týchto vzťahov sú preto rovnaké. Preto je aj právo rovnaké. Teda OV1 / ОВ sa rovná FB1/ OF.
V tejto rovnosti môžu byť segmenty označené bodkami nahradené zodpovedajúcimi fyzikálnymi konceptmi. Takže OV1 Je vzdialenosť od objektívu k obrázku. RH je vzdialenosť od objektu k šošovke. OF - ohnisková vzdialenosť. Segment FB1 sa rovná rozdielu medzi vzdialenosťou k obrázku a zaostrením. Preto ho možno prepísať iným spôsobom:
f / d = (f - F) / F alebo Ff = df - dF.
Na odvodenie vzorca pre tenký objektív musí byť posledná rovnosť delená dfF. Potom sa ukáže:
1 / d + 1 / f = 1 / F.
Má tenký vzorec zberných šošoviek.Divergentná ohnisková vzdialenosť je negatívna. To vedie k zmene rovnosti. Je pravda, že je to bezvýznamné. Je to tak, že vo vzorci tenkého difúzneho objektívu je mínus pred pomerom 1 /F. Tj.
1 / d + 1 / f = - 1 / F.
Stav. Ohnisková vzdialenosť zbernej šošovky je 0,26 m. Je potrebné vypočítať jej zväčšenie, ak je predmet vo vzdialenosti 30 cm.
Riešenie. Malo by sa začať zavedením označení a konverziou jednotiek v C. Takže známe d = 30 cm = 0,3 m a F = 0,26 m. Teraz si musíte vybrať vzorce, hlavný je ten, ktorý je určený na zväčšenie, druhý je na tenkú zbernú šošovku.
Treba ich nejako skombinovať. Aby ste to urobili, budete musieť zvážiť kresbu konštrukcie obrazu v zbernej šošovke. Z takých trojuholníkov je vidieť, že Г = H / h= f / d. To znamená, že na to, aby ste našli zväčšenie, budete musieť vypočítať pomer vzdialenosti k obrázku k vzdialenosti k objektu.
Druhý je známy. Vzdialenosť k obrázku však má byť odvodená z vyššie uvedeného vzorca. Ukazuje sa to
F = dF / (d - F).
Teraz je potrebné tieto dva vzorce skombinovať.
Г = dF / (d(d - F)) = F / (d - F).
V tomto momente je riešenie problému pre vzorec pre tenký objektív redukované na elementárne výpočty. Zostáva nahradiť známe hodnoty:
G = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Odpoveď: Objektív sa zväčšuje 6,5 -krát.

Stav. Lampa je umiestnená jeden meter od zbernej šošovky. Obraz jeho špirály sa získa na obrazovke vzdialenej 25 cm od šošovky. Vypočítajte ohniskovú vzdialenosť určenej šošovky.
Rozhodnutie. Údajne má do údajov zapísať nasledujúce hodnoty: d = 1 m a F = 25 cm = 0,25 m. Tieto informácie postačujú na výpočet ohniskovej vzdialenosti zo vzorca pre tenký objektív.
Takže 1 /F = 1/1 + 1 / 0,25 = 1 + 4 = 5. Úloha však vyžaduje poznať zaostrenie, nie optickú mohutnosť. Preto zostáva len rozdeliť 1 na 5 a získate ohniskovú vzdialenosť:
F = 1/5 = 0,2 m.
Odpoveď: Ohnisková vzdialenosť zbernej šošovky je 0,2 m.
podmienka... Sviečka bola umiestnená vo vzdialenosti 15 cm od zbernej šošovky. Jeho optický výkon je 10 dioptrií. Obrazovka za šošovkou je umiestnená tak, aby na nej bol získaný jasný obraz sviečky. Čomu sa rovná táto vzdialenosť?
Rozhodnutie. Má to byť zapísanie nasledujúcich údajov do krátkeho záznamu: d = 15 cm = 0,15 m, D = 10 dioptrií. Vyššie uvedený vzorec by mal byť napísaný s malou zmenou. Totiž, na pravej strane rovnosti, polož D namiesto 1 /F.
Po niekoľkých transformáciách sa získa nasledujúci vzorec pre vzdialenosť od objektívu k obrázku:
F = d / (dD - jeden).
Teraz musíte nahradiť všetky čísla a počítať. Ukazuje sa, že takáto hodnota pre f: 0,3 m.
Odpoveď: Vzdialenosť od objektívu k obrazovke je 0,3 m.

Stav. Objekt a jeho obraz sú od seba vo vzdialenosti 11 cm. Zberná šošovka poskytuje trojnásobné zväčšenie. Nájdite jeho ohniskovú vzdialenosť.
Rozhodnutie. Vzdialenosť medzi objektom a jeho obrazom je vhodne označená písmenom L = 72 cm = 0,72 m. Zväčšenie G = 3.
Tu sú možné dve situácie.Prvá je, že predmet je za zaostrením, to znamená, že obraz je skutočný. V druhom je predmet medzi ohniskom a objektívom. Potom je obrázok z tej istej strany ako predmet a je imaginárny.
Uvažujme o prvej situácii. Objekt a obrázok sú na opačných stranách zbernej šošovky. Tu môžete napísať nasledujúci vzorec: L = d + f. Druhá rovnica má byť napísaná: Г = F / d. Sústavu týchto rovníc je potrebné vyriešiť dvoma neznámymi. Ak to chcete urobiť, vymeňte ho L o 0,72 m a G o 3.
Z druhej rovnice vyplýva, že F = 3d. Potom sa prvý transformuje takto: 0,72 = 4d. Je ľahké počítať d = 0,18 (m). Teraz je ľahké ho definovať F = 0,54 (m).
Zostáva použiť vzorec tenkých šošoviek na výpočet ohniskovej vzdialenosti. F = (0,18 x 0,54) / (0,18 + 0,54) = 0,135 (m). Toto je odpoveď na prvý prípad.
V druhej situácii je obraz imaginárny a vzorec pre L bude iný: L = F - d. Druhá rovnica pre systém bude rovnaká. Keď argumentujeme podobne, zistíme to d = 0,36 (m) a F = 1,08 (m). Podobný výpočet ohniskovej vzdialenosti poskytne nasledujúci výsledok: 0,54 (m).
Odpoveď: Ohnisková vzdialenosť objektívu je 0,135 m alebo 0,54 m.
Dráha lúčov v tenkej šošovke je dôležitápraktické využitie geometrickej optiky. Koniec koncov, používajú sa v mnohých zariadeniach, od jednoduchých lupov až po presné mikroskopy a teleskopy. Preto je potrebné o nich vedieť.
Odvodený vzorec tenkej šošovky umožňuje riešenieveľa úloh. Okrem toho vám umožňuje vyvodiť závery o tom, aký obraz poskytujú rôzne typy šošoviek. V tomto prípade stačí poznať jeho ohniskovú vzdialenosť a vzdialenosť od objektu.


























