Vlastnosti a metódy hľadania koreňov kvadratickej rovnice

Svet je usporiadaný tak, že riešenie veľkého počtuproblémy sa redukuje na nájdenie koreňov kvadratickej rovnice. Korene rovníc sú dôležité pre opis rôznych vzorcov. To vedeli dokonca aj zememerači v starovekom Babylone. Astronómovia a inžinieri boli nútení vyriešiť aj tieto problémy. V 6. storočí n. L. Indický vedec Aryabhata vyvinul základy pre nájdenie koreňov kvadratickej rovnice. Vzorce nabrali v 19. storočí hotový vzhľad.

Všeobecné pojmy

Odporúčame vám, aby ste sa zoznámili so základnými zákonmi kvadratických rovností. Vo všeobecnosti možno rovnosť napísať takto:

ach² + bx + c = 0,

Počet koreňov kvadratickej rovnice môže byť jeden alebo dva. Rýchlu analýzu je možné vykonať pomocou pojmu diskriminátory:

D = b² - 4ac

V závislosti od vypočítanej hodnoty dostaneme:

• Pre D> 0 existujú dva rôzne korene. Všeobecný vzorec na určenie koreňov kvadratickej rovnice vyzerá (-b ± √D) / (2a).
• D = 0, v tomto prípade je koreň jedna a zodpovedá hodnote x = -b / (2a)
• D <0, neexistuje riešenie rovnice pre zápornú hodnotu diskriminátora.

Poznámka: ak je diskriminant negatívny, rovnica nemá korene iba v oblasti. Ak je algebra rozšírená o koncept komplexných koreňov, potom má rovnica riešenie.

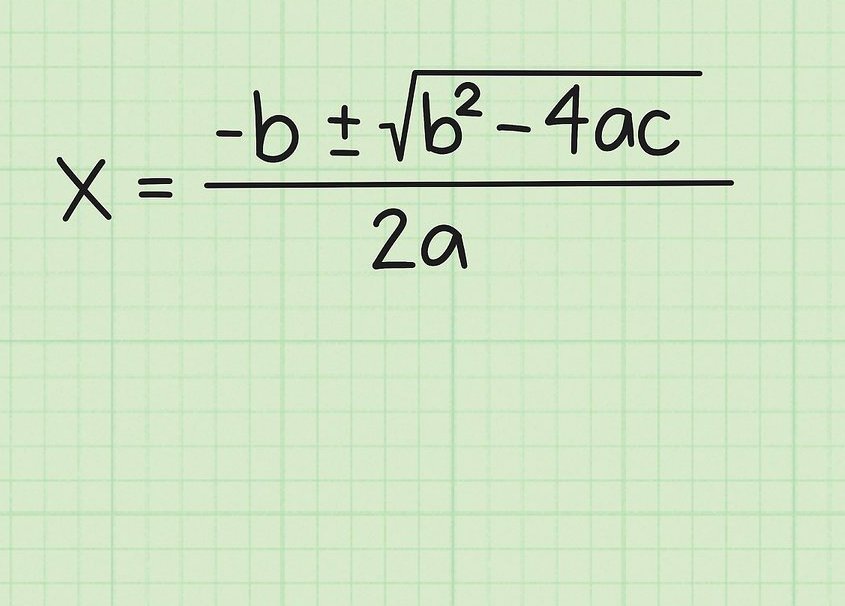
Tu je reťazec akcií potvrdzujúcich vzorec na nájdenie koreňov.

Zo všeobecnej podoby rovnice vyplýva:

ach² + bx = -c

Vynásobte pravú a ľavú stranu číslom 4a a pridajte b², dostaneme

4a²s² + 4abx + b² = -4ac + b²

Transformujte ľavú stranu ako štvorcový polynóm (2ax + b)²... Vezmite druhú odmocninu z oboch strán rovnice 2ax + b = -b ± √ (-4ac + b²), prenesieme koeficient b na pravú stranu, dostaneme:

2ax = -b ± √ (-4ac + b²)

To znamená:

x = (-b ± √ (b² - 4ac))

Čo bolo potrebné ukázať.

Špeciálny prípad

V niektorých prípadoch je možné riešenie problému zjednodušiť. Takže pre párny koeficient b dostaneme jednoduchší vzorec.

Označíme k = 1 / 2b, potom vzorec všeobecnej formy koreňov kvadratickej rovnice má tvar:

x = (-k ± √ (k² - ac)) / a

Pre D = 0 dostaneme x = -k / a

Ďalším špeciálnym prípadom bude riešenie rovnice pre a = 1.

Pre pohľad x² + bx + c = 0, korene budú x = -k ± √ (k² - c) keď je diskriminant väčší ako 0. V prípade, keď D = 0, koreň bude určený jednoduchým vzorcom: x = -k.

Použitie grafov

Každý človek, bez toho, aby o tom vedel, sa neustále stretáva s fyzikálnymi, chemickými, biologickými a dokonca sociálnymi javmi, ktoré sú dobre popísané kvadratickou funkciou.

Poznámka: Krivka založená na kvadratickej funkcii sa nazýva parabola.

Tu je niekoľko príkladov.

1. Pri výpočte trajektórie strely sa používa vlastnosť pohybu pozdĺž paraboly telesa vystreleného pod uhlom k horizontu.
2. Vlastnosť paraboly na rovnomerné rozloženie záťaže je v architektúre široko používaná.

Pochopme dôležitosť parabolickej funkcie a poďme zistiť, ako pomocou grafu skúmať jeho vlastnosti pomocou pojmov „diskriminačný“ a „korene kvadratickej rovnice“.

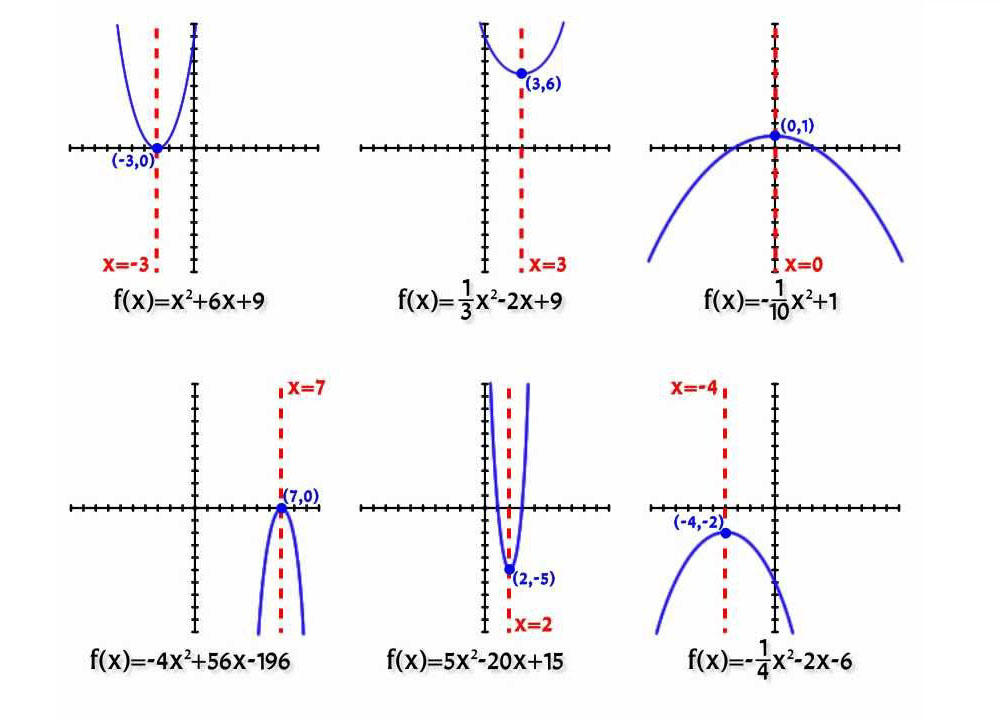
V závislosti od hodnoty koeficientov a a b existuje pre polohu krivky iba šesť možností:

1. Diskriminant je pozitívny, a a b majú rôzne znaky. Vetvy paraboly smerujú nahor, kvadratická rovnica má dve riešenia.
2. Diskriminant a koeficient b sa rovnajú nule, koeficient a je väčší ako nula. Graf je v kladnej zóne, rovnica má 1 koreň.
3. Diskriminačný a všetky koeficienty sú pozitívne. Kvadratická rovnica nemá riešenie.
4. Rozdiel a koeficient a sú záporné, b je väčšie ako nula. Vetvy grafu smerujú nadol, rovnica má dva korene.
5. Diskriminant a koeficient b sa rovnajú nule, koeficient a je záporný. Parabola sa pozerá nadol, rovnica má jeden koreň.
6. Diskriminačný a všetky koeficienty sú negatívne. Neexistujú žiadne riešenia, hodnoty funkcií sú úplne v negatívnej zóne.

Poznámka: možnosť a = 0 sa neberie do úvahy, pretože v tomto prípade parabola degeneruje do priamky.

Všetky vyššie uvedené skutočnosti dobre ilustruje nasledujúci obrázok.

Príklady riešenia problémov

Podmienka: pomocou všeobecných vlastností vytvorte kvadratickú rovnicu, ktorej korene sú navzájom rovnaké.

riešenie:

podľa stavu problému x₁ = x₂alebo -b + √ (b² - 4ac) / (2a) = -b + √ (b² - 4ac) / (2a). Zjednodušenie zadávania:

-b + √ (b² - 4ac) / (2a) - (-b - √ (b² - 4ac) / (2a)) = 0, otvorte zátvorky a zadajte podobné výrazy. Rovnica má tvar 2√ (b² - 4ac) = 0. Toto tvrdenie platí, ak b² - 4ac = 0, preto b² = 4ac, potom sa do rovnice dosadí hodnota b = 2√ (ac)

ach² + 2√ (ac) x + c = 0, v redukovanej forme dostaneme x² + 2√ (c / a) x + c = 0.

odpoveď:

pre a nerovná sa 0 a akékoľvek c existuje iba jedno riešenie, ak b = 2√ (c / a).

Kvadratické rovnice napriek ich jednoduchostimajú veľký význam v technických výpočtoch. Takmer každý fyzikálny proces je možné popísať s určitou aproximáciou pomocou mocnino-právnych funkcií rádu n. Kvadratická rovnica bude prvou takouto aproximáciou.