
Да бисте креирали било који програм, требају вам основниалгоритамске конструкције. Следи најједноставнији начин решавања проблема. Може се користити, на пример, за рад са примерима истог типа. Постоје и друге врсте: гранање и петљање. О њима ће бити речи у овом чланку. Али прво морате да схватите који је алгоритам у целини.
Реч „алгоритам“ потиче од латинског алгоритми.Шта то значи? Аутентична реч потиче од имена математичара, чија је делатност пала у 9. век. Захваљујући расправи о ал-Хваризмију, човечанство је успело да се упозна са основном врстом алгоритамске конструкције и, уопште, са општим концептом.
Раније је усвојен облик писања речи - „алгоритам“. Сада се користи само у неколико случајева.
Алгоритам је процес који значи променупочетни подаци који се јављају у облику дискретних корака. Свака особа се у животу сусреће са овим концептом, ко год да је. Алгоритмима се можемо назвати припрема чаја или хране, множење или сабирање, решавање једначина итд. Сви кућански апарати, чији је радни процес аутоматизован, функционишу захваљујући јасним корацима уписаним у меморију процесора. Такви алгоритми се називају кућним алгоритмима. Постоје и друге врсте. Размотримо их.
Главне алгоритамске конструкције подељене су у неколико типова, о чему ће бити речи у овом пододељку. Шта су они?
У основи је алгоритам прецизан до најмањегдетаљи упутства. Међутим, не могу се сви такви подаци назвати описаним концептом. Да бисте разумели да ли је алгоритам инструкција или не, требало би да га проверите за одређена својства.
Све основне алгоритамске конструкције морају имати радње које им се „покоравају“. Размотримо ово питање детаљније.
Ако у потпуности пратите рад алгоритама и њиховихсвојства, можете видети да није неопходно разумети њихове компоненте, сасвим јасно одговарају плану. Добиће се тачан резултат, чак и ако се само механички придржавате неопходних радњи. Из овога можемо закључити да је због недостатка значења у свести о радњама сасвим могуће дати алгоритам имплементацији рачунара. Другим речима, овај поступак је потребан за аутоматизоване уређаје.
Које особине би требало да имају основне алгоритамске конструкције за најтачнији рад?
Ако говоримо о методама писања алгоритама, онда треба истаћи следеће:
Треба разјаснити последњу тачку.Шта је блок дијаграм? То је линеарни или нелинеарни алгоритам чији су кораци написани помоћу посебних блокова. Они имају своју конфигурацију, сврху и функцију. У случају таквог описа, алгоритам се записује у блок дијаграме, који су међусобно повезани линијама. Морају додатно снимити једну или другу радњу (корак).

Неки тврде да алгоритми немају 3тип и 4. Основне алгоритамске конструкције: линеарна, разграната, циклична. Шта је разлог ове заблуде није јасно. Међутим, за једноставно решење сложених проблема, рачунар користи алгоритме ове три прилично велике групе. Размотримо их.
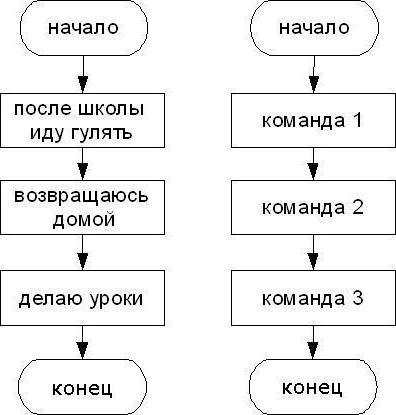
Треба напоменути да су све главне алгоритамске конструкције (праћење, гранање, петља) међусобно повезане, иако се могу користити засебно.
Шта је потребно за стварање циклуса?
Петље могу бити детерминистичке иитеративни. Прва је понављање радњи са познатим бројем понављања. Итеративна петља је она која се понавља неограничено много пута док услов не постане тачан или нетачан.
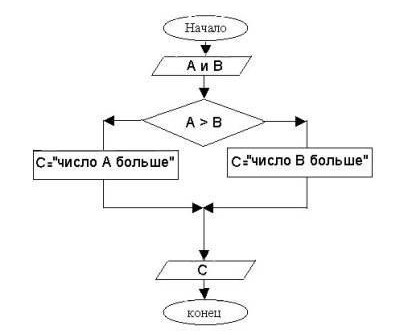
Вриједно је запамтити да је главниосновни алгоритам се не односи на алгоритамске конструкције. Какав је он Овај концепт већ дуго није пронађен у савременој литератури, али то не значи да више уопште не постоји. С обзиром да се у решавању проблема може појавити неколико грана или понављања, може се истаћи следећи закључак. Основне алгоритамске конструкције (линеарне, разгранате, цикличне) су основне. У ствари, они представљају „структурну целину“ сваке такозване инструкције.
Као што је већ јасно из горе наведеног, алгоритмипостоје линеарни и нелинеарни. Размотримо прву опцију. Зашто се тако зове? Све је крајње једноставно. Чињеница је да све радње које се репродукују у алгоритму имају јасно секвенцијално извршење, сви кораци се изводе строго један за другим. Такви задаци су по правилу мали и имају низак ниво сложености.
Пример линеарног алгоритма био би поступак прављења чаја:
Програмирање основних алгоритамских конструкција је довољно тешко, али када је реч о линеарним алгоритмима, често је врло лако применити их.

Како знати да ли се алгоритам грана?Довољно је осигурати избор између две или више опција за деловање, у зависности од тога да ли је услов испуњен или не. Свака стаза назива се грана.
Главна карактеристика алгоритма гранања је постојање условне гране. Појављује се када се израз тестира на тачно или нетачно.
Типично, логички изрази су представљени сазнаци „мање од“, „веће од“, „мање или једнако“, „веће или једнако“, „једнако“, „није једнако“. Понекад постоје варијанте у којима је стање међусобно повезано помоћу наредби и (и) и или (или).
Пример таквог алгоритма може бити решењеследећи задатак: ако је израз ((к + 3) / 1) једнак позитивном броју, онда на екрану прикажите резултат, ако је негативан, обавестите корисника о грешци.
Прилично је једноставно користити основне алгоритамске конструкције у пракси. Разгранавање је једна од најчешћих метода решења.
Бројач циклуса - циклус који укључујепроменљива која вредност мења у корацима. Корак поставља корисник или га програмер записује приликом писања софтвера. Већина језика користи изјаву фор за такву петљу.
Да би програм приказао два реда 4 пута:
Морате створити детерминистичку петљу. Како то изгледа? Користимо језик Пасцал за бољу перцепцију структуре.
1. За и: = 1 до 2 урадите:
- и је бројач петље, он је тај који одређује број понављања у петљи.
2. Почните (заграде оператора се отварају тако да су обе фразе тело петље и понављају се заједно.)
3. Напишите („Како сте?“):
- реч врителн значи излаз фразе у појединачним наводницима.
4. Врителн ("У реду, хвала").
5. Крај.
6.и: = и + 1.
Као што видите, прилично је лако, па чак и занимљиво користити основне алгоритамске конструкције. Основни алгоритми су заиста широко познати, без њих је немогуће писати програме.

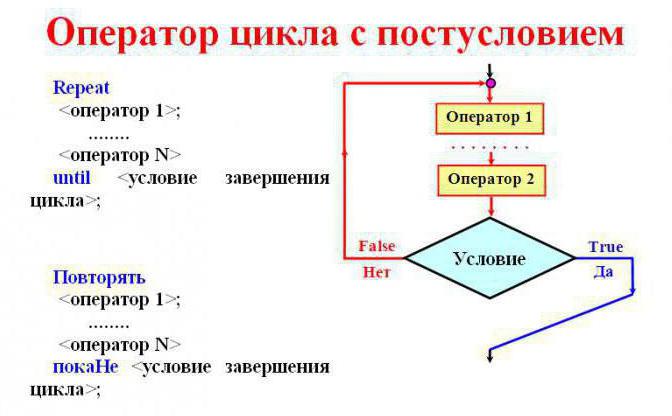
Петља са постусловом се може поновитинеодређени број радњи без уметања заграда оператора или сложених речи у њих. Дефинитивно ће се извршити бар једном. Петља ради док је услов нетачан. Престаје када индикатори постану тачни. Алгоритам је заснован на овоме. Основни алгоритамски конструкти овог типа делују управо овим темпом.
Да би се спровео овај циклус, потребна је конструкцијаПонављајте А до Б. Дословно се преводи као „понављање радњи док је услов нетачан“. Сходно томе, кроз А се изражава сам поступак понављања, кроз Б - податке, који би као резултат требало да поприме тачну вредност.
Петља са постусловом конструисана је тако дау сваком случају се извршава најмање једном. Међутим, постоје случајеви када је циклус неопходан у случају одређеног стања, а у његовом одсуству понављање не би требало вршити. У супротном, резултат ће бити нетачан. Овде се користи петља предуслова. Да бисте је креирали, потребна вам је конструкција „док А до Б“. Прва команда се дословно преводи као „ћао“. А - услов и Б - радње које ће се поновити. Цела конструкција значи: „све док је услов тачан, изводите радње“.
Сви основни алгоритамски конструкти радесамо у одређеним случајевима. Какви су у петљи са предусловом? Ако требате поновити више од једне радње, али неколико одједном, требало би да користите сложене операторе или посебне заграде. Петља може пропасти ако, приликом уласка у њу, услов није тачан. Сходно томе, радње ће се поновити ако је тачно.

Помоћни алгоритам се користи у другимобрађује наводећи само његово име. Не припада главним алгоритамским конструкцијама. У програмским језицима такав процес радњи назива се потпрограмом. Да би се олакшао рад са кодом и последично лакше решавање проблема, свака радња се комбинује у један блок, што је помоћни алгоритам. Сваком од њих се може дати име, што вам омогућава да се касније на њега више пута позивате.


























