
Geometri çok yönlü bir bilimdir.Mantık, hayal gücü ve zeka geliştirir. Tabii ki, karmaşıklığı ve çok sayıda teorem ve aksiyom nedeniyle, okul çocukları her zaman hoşlanmıyor. Ek olarak, genel kabul görmüş standartları ve kuralları kullanarak bulgularını sürekli kanıtlamaya ihtiyaç vardır.

köşeleri Eğitim
Herhangi bir açı iki kesişme tarafından oluşturulurbir noktadan iki ışın yönlendirmek veya tutmak. Bir harf ya da üç olarak adlandırılabilirler ve bunlar art arda açının yapım noktalarını gösterir.
Açılar derece cinsinden ölçülür veanlamlarından) farklı denir. Yani, keskin, kör ve konuşlu bir dik açı var. İsimlerin her biri belirli bir derece ölçüsüne veya aralığına karşılık gelir.
Geniş bir açı 90 dereceden büyük.
Derecesi 90 ise açı doğrudan denir.
Tek bir katı çizgi ile oluşturulmuş ve derece ölçüsü 180 olduğunda, genişletilmiş olarak adlandırılır.
Komşu köşeleri
Ortak tarafı olan köşeleri, ikinci tarafıbirbirlerine devam eden, bitişik denir. Keskin veya donuk olabilirler. Açılma açısının çizgi ile kesişmesi bitişik açıları oluşturur. Özellikleri şöyle:
Bu özellikler sayesinde, açının derecesini, başka bir açının değerine veya en azından aralarındaki orana sahip olarak hesaplayabilirsiniz.

Kenarları birbirinin bir devamı olan açılara dikey denir. Böyle bir çift, çeşitlerinden herhangi biri olabilir. Dikey açılar daima eşittir.
Çizgilerin kesişiminde oluşurlar. Onlarla birlikte daima mevcut ve bitişik köşeler bulunur. Açı eşzamanlı olarak birine bitişik olabilir ve diğerine dikey olabilir.
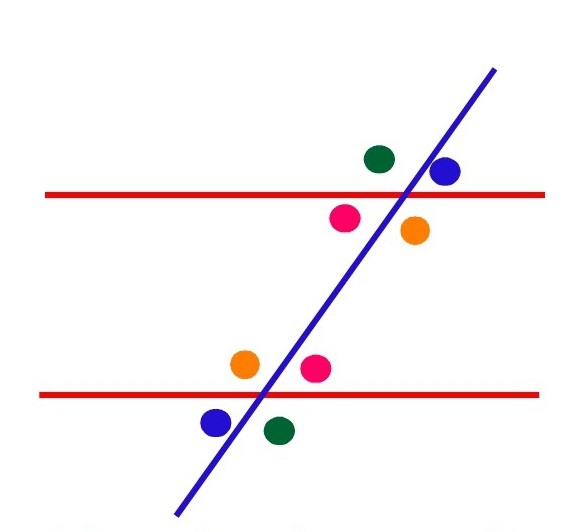
Paralel rastgele paralel çizgilerden geçerkenBu çizgi ayrıca birkaç farklı açı tipini de göz önünde bulundurur. Böyle bir çizgi bir sekant olarak adlandırılır ve karşılık gelen, tek taraflı ve çaprazlamasına uzanan köşeleri oluşturur. Birbirlerine eşittirler. Dikey ve bitişik açıları olan özellikler ışığında düşünülebilir.
Yani köşelerin teması güzel görünüyorbasit ve anlaşılır. Tüm özelliklerinin hatırlanması ve ispatlanması kolaydır. Köşeler sayısal bir değere denk geldiği sürece problem çözme karmaşık görünmez. Ayrıca, günah ve cos çalışması başladığında, birçok karmaşık formülü, sonuçlarını ve sonuçlarını ezberlemek gerekecektir. O zamana kadar, bitişik açıları bulmanız gereken basit görevlerin tadını çıkarabilirsiniz.


























