
Üçgen geometrik bir şekildir.düzlemde tek bir düz çizgi üzerinde bulunmayan çizgilerle birbirine bağlanmış üç nokta. Bir üçgenin köşeleri, açıların tabanındaki noktalardır ve onları birleştiren çizgilere üçgenin kenarları denir. Böyle bir şeklin alanını belirlemek için, üçgenin içi sıklıkla kullanılır.
Farklı olan üçgenlere ek olarakişte eşkenar, yani iki özdeş taraf var. Figürün tabanı - onlar ve diğer taraf olarak adlandırılır. Bu tür çokgenlerin başka bir türü daha var - eşkenar. Yanlarının üçü de aynı uzunluktadır.
Üçgenler için, bir derece ölçüm sistemi doğaldır. Bu rakamların farklı açıları olabilir, bu nedenle aşağıdaki gibi sınıflandırılır:
Daha önce de belirtildiği gibi, bir üçgençokgenler, üç köşesi ve onları birleştiren düz çizgiler vardır. Çizgiler genellikle aynı şekilde işaretlenir: küçük Latin harfleriyle köşeler ve karşılık gelen büyük harfte her birinin karşı tarafları.
Bir üçgenin tüm köşelerini toplarsanız, toplam 180 derece elde edersiniz. İç açıyı bulmak için 180'den derece ile üçgenin dış açısının değerini çıkarın. Dışarıdaki açının ne olduğunu bulmak için içinden iki ayrı açıyı katlamaya değer.

Her üçgende keskin veya donuk muaçıları, büyük köşenin karşısındaki en büyük taraftır. Köşeler arasındaki düz çizgiler aynıysa, buna göre her açı 60 derecedir.
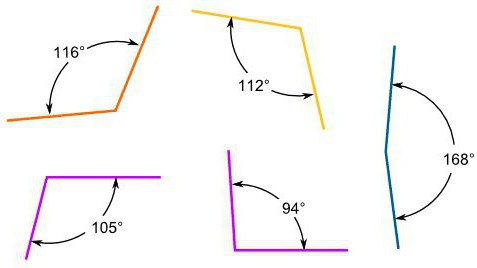
Bir üçgenin geniş açısı her zaman 90 derecelik bir açıdan daha büyüktür, ancak katlanmamış bir açıdan daha azdır. Böylece, geniş açı 90 ila 180 derecedir.
Soru ortaya çıkıyor: böyle bir şekilde birden fazla geniş açı var mı? Cevap yüzeydedir: hayır, çünkü açıların toplamı 180'den az olmalıdır0. Eğer iki açı örneğin 95 derecede ise, o zaman üçüncü açı bulunamaz.
İki geniş çokgen eşittir:
Geniş açılı tüm üçgenlerçizgiler harika denir. Birincisi yükseklik. Köşelerden birinden ona karşılık gelen tarafa diktir. Bütün yükseklikler bir orkenter adı verilen bir noktada çarpışır. Geniş açılı bir üçgende, şeklin kendisinin dışında yer alacaktır. Keskin köşelere gelince, merkez üçgenin kendisinde.
Başka bir çizgi medyan. Bu, karşılık gelen tarafın tepesinden merkezine doğru çizilen bir çizgidir. Tüm medyanlar bir üçgende birleşir ve kombinasyonlarının yeri böyle bir çokgenin ağırlık merkezidir.

Bisektör, hem geniş açıları hem de gerisini ikiye bölen bir çizgidir. Bu tür üç çizginin kesişimi her zaman sadece şeklin kendisinde gerçekleşir ve üçgende yazılı dairenin merkezi olarak tanımlanır.
Buna karşılık, dairenin merkezi etrafında dönüyordurakamlar üç medyan dikten elde edilebilir. Bunlar, köşeleri birleştiren çizgilerin orta noktalarından düşürülen çizgilerdir. Üç orta dik üçgenin geniş açılara sahip bir üçgende kesişimi şeklin dışında bulunur.


























