Властивості і способи пошуку коренів квадратного рівняння

Світ влаштований так, що рішення великої кількостізадач зводиться до знаходження коренів квадратного рівняння. Коріння рівнянь мають важливе значення для опису різних закономірностей. Це було відомо ще землемірам стародавнього Вавилона. Астрономи і інженери теж були змушені вирішувати такі завдання. Ще в VI столітті нашої ери індійський вчений Аріабхата розробив основи знаходження коренів квадратного рівняння. Формули придбали закінчений вигляд в XIX столітті.

загальні поняття

Пропонуємо ознайомитися з основними закономірностями квадратичних рівності. У загальному вигляді рівність може бути записано так:

ах² + Bx + c = 0,

Число коренів квадратного рівняння може дорівнювати одному або двом. Швидкий аналіз можна провести, використовуючи поняття дискримінант:

D = b² - 4ac

Залежно від обчисленого значення отримуємо:

• При D> 0 існують два різних кореня. Формула в загальному вигляді для визначення коренів квадратного рівняння виглядає як (-b ± √D) / (2a).
• D = 0, в цьому випадку корінь один і відповідає значенню x = -b / (2a)
• D <0, для від'ємного значення дискримінанту рішення рівняння не існує.

Зауваження: якщо дискримінант від'ємний, рівняння не має коренів тільки в області дійсних чисел. Якщо алгебру розширити до поняття комплексних коренів, то рівняння має рішення.

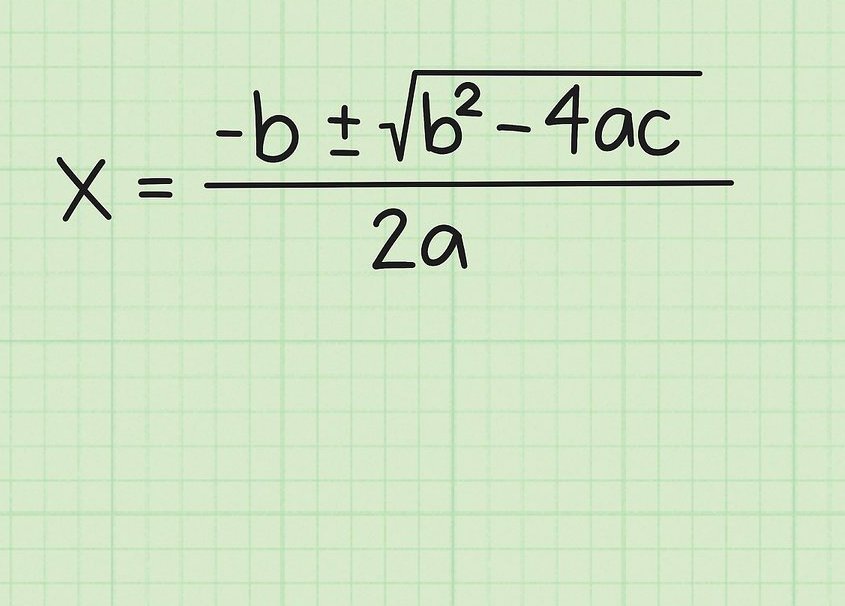
Наведемо ланцюжок дій, що підтверджує формулу знаходження коренів.

З загального вигляду рівняння, слід:

ах² + Bx = -c

Праву і ліву частини множимо на 4a і додаємо b², отримуємо

4a²з² + 4abx + b² = -4ac + b²

Перетворимо ліву частину у вигляді квадрата многочлена (2ax + b)². Витягуємо квадратний корінь з обох частин рівняння 2ax + b = -b ± √ (-4ac + b²), Переносимо коефіцієнт b в праву частину, отримаємо:

2ax = -b ± √ (-4ac + b²)

Звідси випливає:

x = (-b ± √ (b² - 4ac))

Що й треба було показати.

Окремий випадок

У деяких випадках рішення задачі може спроститися. Так, при парному коефіцієнті b отримаємо більш просту формулу.

Позначимо k = 1 / 2b, тоді формула загального вигляду коренів квадратного рівняння набуває вигляду:

x = (-k ± √ (k² - ac)) / a

При D = 0, отримуємо x = -k / a

Іншим окремим випадком буде рішення рівняння при a = 1.

Про людське око x² + Bx + c = 0 корені будуть x = -k ± √ (k² - c) при дискримінант більше 0. Для випадку коли D = 0, корінь буде визначатися простою формулою: x = -k.

Використання графіків

Будь-яка людина, навіть не підозрюючи цього, постійно стикається з фізичними, хімічними, біологічними і навіть соціальними явищами, які добре описуються квадратичною функцією.

Зауваження: крива, побудована на підставі квадратичної функції, отримала назву параболи.

Наведемо кілька прикладів.

1. При розрахунку траєкторії польоту снаряда використовують властивість руху по параболі тіла, випущеного під кутом до горизонту.
2. Властивість параболи рівномірно розподіляти навантаження широко використовується в архітектурі.

Розуміючи всю важливість параболічної функції, розберемося, як за допомогою графіка досліджувати її властивості, використовуючи поняття "дискриминант" і "коріння квадратного рівняння".

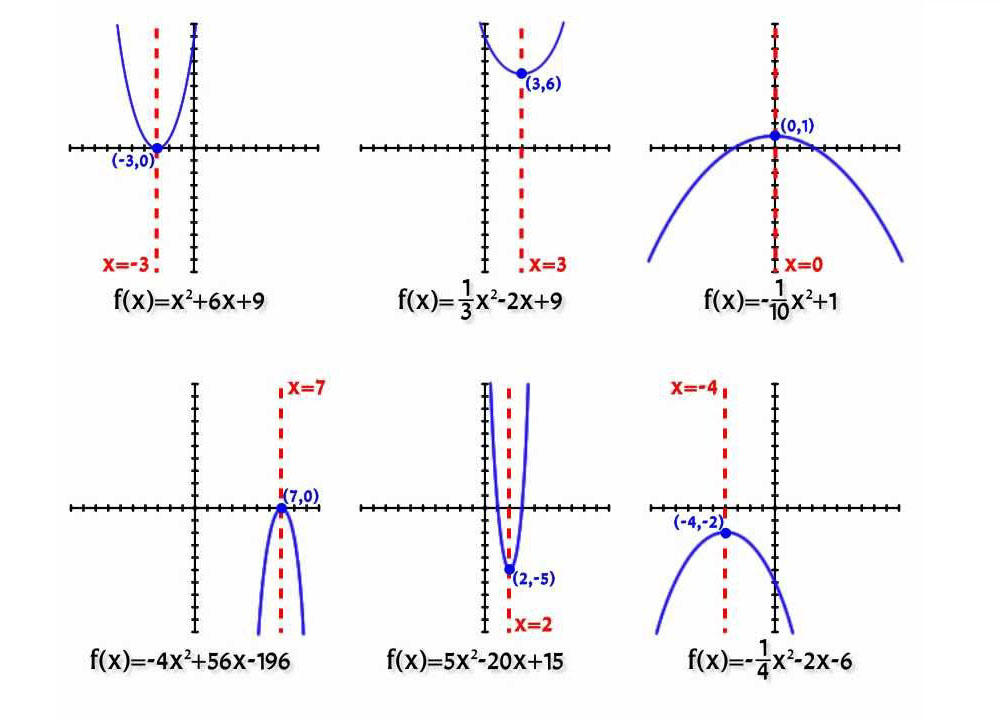
Залежно від величини коефіцієнтів a і b, існує всього шість варіантів положення кривої:

1. Дискримінант позитивний, a і b мають різні знаки. Гілки параболи дивляться вгору, у квадратичного рівняння два рішення.
2. Дискримінант і коефіцієнт b дорівнюють нулю, коефіцієнт a більше нуля. Графік розташований в позитивній зоні, рівняння має 1 корінь.
3. Дискримінант і всі коефіцієнти мають позитивні значення. У квадратичного рівняння немає рішення.
4. Дискримінант і коефіцієнт а - негативні, b - більше нуля. Гілки графіка спрямовані вниз, у рівняння два кореня.
5. Дискримінант і коефіцієнт b дорівнюють нулю, коефіцієнт a - негативний. Парабола дивиться вниз, у рівняння один корінь.
6. Значення дискримінанту і всіх коефіцієнтів - негативні. Рішень немає, значення функції повністю в негативній зоні.

Зауваження: варіант a = 0 не розглядається, тому що в цьому випадку парабола вироджується в пряму.

Все сказане добре ілюструє малюнок, представлений нижче.

Приклади розв'язання задач

Умова: використовуючи загальні властивості, складіть квадратне рівняння, корені якого рівні між собою.

Рішення:

за умовою завдання x₁ = x₂, Або -b + √ (b² - 4ac) / (2a) = -b + √ (b² - 4ac) / (2a). Спрощуємо запис:

-b + √ (b² - 4ac) / (2a) - (-b - √ (b² - 4ac) / (2a)) = 0, розкриваємо дужки і наводимо подібні члени. Рівняння набуває вигляду 2√ (b² - 4ac) = 0. Це твердження вірне, коли b² - 4ac = 0, звідси b² = 4ac, тоді значення b = 2√ (ac) підставляємо в рівняння

ах² + 2√ (ac) x + c = 0, в наведеному вигляді отримуємо x² + 2√ (c / a) x + c = 0.

відповідь:

при a не в рівному 0 і будь-якому c існує тільки одне рішення, якщо b = 2√ (c / a).

Квадратні рівняння при всій своїй простотімають велике значення в інженерних розрахунках. Практично будь-який фізичний процес можна описати з деяким наближенням, використовуючи статечні функції порядку n. Квадратне рівняння буде першим таким наближенням.