
Počítačová věda jako věda o metodách sběru,objednání a zpracování různých dat začíná jeho vývoj v polovině dvacátého století. Ačkoli někteří historici věří, že tvorba počítačové vědy začala v 17. století, s vynálezem první mechanické kalkulačky, nejvíce spojit to s dobou pokročilejšího počítače. Ve 40. letech 20. století, s příchodem prvních počítačů, získala informatika nový impuls ve vývoji.
Bylo to s příchodem prvních počítačůbylo třeba vyvinout nové metody systematizace, výpočtu a zpracování velkého množství dat a také vyvinout algoritmy, které by umožnily plně využívat potenciál nových počítačů. Počítačová věda získala status nezávislé vědecké disciplíny a přesunula se z roviny matematických výpočtů ke studiu výpočetní techniky jako celku.

Вся современная компьютерная наука базируется на logické operace. Lze je nazvat základní složkou. V programovacích počítačových systémech je koncept logické operace určitou akcí, po které je vygenerován nový koncept nebo hodnota, která je vytvořena na základě existujících konceptů. Sada takových akcí se může lišit v závislosti na elementu procesoru, který musí provádět příkazy. Existují však některé operace, které jsou společné téměř všem existujícím systémům. Jsou to operace, které pracují s obsahem samotných významů, například negace, nebo ty, které mění kvantitativní charakteristiku pojmu - sčítání, odčítání, násobení, dělení.
Protože algebra logiky zahrnuje práciabstraktní pojmy, pak zobecněné datové typy fungují jako operandy všech logických operací. Klasické prvky, s nimiž výroková algebra pracuje, jsou výroky, nepravdivé nebo pravdivé. V elektronice a programování se k popisu těchto termínů používají booleovské proměnné true a false nebo celočíselné hodnoty 1 (true) a 0 (false). Kombinace těchto hodnot, bez ohledu na to, jak neuvěřitelně může znít, je spojena s prací nejsložitějších a rozsáhlých systémů. Veškerý programový kód, který běží na počítači nebo na jakémkoli digitálním zařízení, je dynamicky převeden do posloupnosti nul a nul - univerzálního kódu, který může zpracovat jakýkoli procesor.
Как было уже сказано ранее, в классической Booleovská algebra, existují 2 typy funkcí. Základní logické operace u binárních datových typů jsou akce, které ovlivňují samotný příkaz (unární nebo unární operace). To také zahrnuje operace, které generují nové příkazy na základě existujících hodnot (binární operace nebo dvojité). Pořadí logických operací je stejné jako při provádění matematických výpočtů: zleva doprava, s přihlédnutím k závorkám.

Nejjednodušší a jeden z nejslavnějšíchfunkce logické logiky je negační funkce. Tato nejjednodušší logická operace je opačnou hodnotou vstupního operandu. V elektronice se tato akce někdy nazývá inverze. Pokud například převrátíte výrok „pravda“, bude výsledek „nepravdivý“. A naopak - negace smyslu „nepravdivé“ povede k významu „pravdy“. Taková logická operace v programování se velmi často používá pro větvení algoritmů a implementaci „výběru“ následné sady příkazů na základě existujících výsledků nebo změněných podmínek.
V programování a informatice se používáomezená sada binárních (binárních) operací. Oni dostali jejich jméno od latinského slova bi, znamenat “dva”, a být druh funkce, která vezme dva argumenty na vstupu a jako výsledek vrací jednu novou hodnotu. Tabulky pravdy se používají k popisu všech funkcí booleovské algebry.
Tento systém je navržen pro konkrétnípočet vstupních operandů a popisuje všechny výsledné hodnoty, které se daná logická operace může vrátit se zadanou sadou vstupních parametrů.
Nejčastěji používanými funkcemi v oblasti informatiky a výpočetní techniky jsou operace logického sčítání (disjunkce) a logického násobení (spojení).
Logická operace „AND“ je funkcí volbynejmenší ze dvou nebo n vstupních operandů. Na vstupu může mít tato funkce dvě (binární funkce), tři hodnoty (ternární) nebo neomezený počet operandů (n-ary operace). Při výpočtu výsledku funkce bude nejmenší ze zadaných vstupních hodnot.
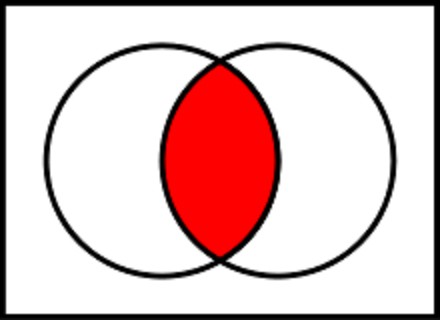
Funkce v běžné algebře je funkcenásobení. Proto se operace spojování často nazývá logickým násobením. Při psaní funkce je znaménkem buď znaménko násobení (tečka) nebo ampersant. Pokud pro tuto funkci sestavíte tabulku pravdy, uvidíte, že funkce vezme hodnotu „true“ nebo 1, pouze pokud jsou všechny vstupní operandy pravdivé. Pokud se alespoň jeden ze vstupních parametrů rovná nule nebo hodnotě „false“, bude výsledek funkce také „false“.

Toto odráží analogii s aritmetickým násobením:vynásobením libovolného čísla a množiny čísel 0 se vždy vrací 0. Tato logická operace je komutativní: pořadí, ve kterém přijímá vstupní parametry, neovlivní konečný výsledek výpočtu.
Další vlastností této funkce jeasociativita nebo kombinace. Tato vlastnost umožňuje nezohlednit pořadí výpočtu při výpočtu sekvence binárních operací. Proto pro 3 nebo více po sobě jdoucích logických multiplikačních operací není třeba uvažovat závorky. Při programování se tato funkce často používá k zajištění toho, aby konkrétní příkazy byly prováděny pouze při splnění určitých podmínek.
Logická operace „NEBO“ - typ booleovské funkce,což je analog algebraického sčítání. Jiné názvy této funkce jsou logické sčítání, disjunkce. Stejně jako operace logického násobení může být disjunkce binární (vypočítat hodnotu na základě dvou argumentů), ternární nebo n-ary.

Tabulka pravdy pro danou logickou operacije druh alternativy ke spojení. Logická operace „NEBO“ vypočítá maximální výsledek z poskytnutých argumentů. Disjunkce vezme hodnotu false na výstup, nebo 0, pouze pokud všechny vstupní parametry přicházejí s hodnotami 0 (false). V každém případě výstup získá hodnotu „true“ nebo 1. K zaznamenání této funkce se nejčastěji používá matematické znaménko sčítání („plus“) nebo dva svislé pruhy. Druhá možnost je běžná ve většině programovacích jazyků a je výhodnější, protože umožňuje jasně oddělit logickou operaci od aritmetické.
Základní logické operace, ať už jsou unárny,binární, ternární nebo jiné funkce podléhají určitým pravidlům a vlastnostem, které popisují jejich chování. Jednou ze základních vlastností logických funkcí popsaných výše je komutativita.

Tato vlastnost zajišťuje, že z permutacena místech operandů se hodnota funkce nemění. Ne všechny operace mají tuto vlastnost. Na rozdíl od spojek a disjunkcí, které splňují požadavky na komutativitu, funkce násobení matice není, a permutace faktorů v této operaci bude mít za následek změnu výsledku i exformaci.
Další důležitou vlastností, která se často používá v elektronice a obvodech, je podřízení párů logických operací zákonům de Morgan.

Tyto zákony spojují dvojice logických operacípomocí funkce logické negace, to znamená, že umožňují vyjádřit jednu logickou operaci pomocí jiné. Například spojovací negační funkce může být vyjádřena disjunkcí negací jednotlivých operandů. Pomocí těchto zákonů lze logické operace „AND“, „OR“ vzájemně vyjádřit a implementovat s minimálními náklady na hardware. Tato vlastnost je velmi užitečná v obvodech, protože vám umožňuje šetřit zdroje při výpočtu a vytváření mikroobvodů.


























