
Η γεωμετρία είναι μια ακριβής και πολύ περίπλοκη επιστήμη,που με όλα αυτά είναι ένα είδος τέχνης. Γραμμές, αεροπλάνα, αναλογίες - όλα αυτά βοηθούν στη δημιουργία πολλών πραγματικά όμορφων πραγμάτων. Και παραδόξως, αυτό βασίζεται στη γεωμετρία στις πιο διαφορετικές μορφές της. Σε αυτό το άρθρο θα εξετάσουμε ένα πολύ ασυνήθιστο πράγμα που σχετίζεται άμεσα με αυτό. Η χρυσή αναλογία είναι ακριβώς η γεωμετρική προσέγγιση που θα συζητηθεί.
Οι άνθρωποι καθοδηγούνται συχνότερα από το σχήμα του αντικειμένου.για να τον αναγνωρίσουμε ανάμεσα σε εκατομμύρια άλλους. Με τη μορφή καθορίζουμε τι είδους πράγματα βρίσκεται μπροστά μας ή στέκεται μακριά. Καταρχάς αναγνωρίζουμε τους ανθρώπους από τα σχήματα του σώματος και του προσώπου τους. Επομένως, μπορούμε να πούμε με σιγουριά ότι το ίδιο το σχήμα, το μέγεθος και η εμφάνισή του είναι ένα από τα πιο σημαντικά πράγματα στην ανθρώπινη αντίληψη.
Για τους ανθρώπους, η μορφή αντιπροσωπεύει τα πάνταενδιαφέρον για δύο βασικούς λόγους: είτε υπαγορεύεται από ζωτική αναγκαιότητα, είτε προκαλείται από αισθητική απόλαυση από την ομορφιά. Η καλύτερη οπτική αντίληψη και η αίσθηση της αρμονίας και της ομορφιάς συχνότερα έρχεται όταν ένα άτομο παρατηρεί ένα σχήμα στην κατασκευή του οποίου χρησιμοποιήθηκε η συμμετρία και μια ειδική αναλογία, που ονομάζεται χρυσός λόγος.
Έτσι, η χρυσή αναλογία είναι η χρυσή αναλογία,που είναι επίσης αρμονική διαίρεση. Για να το εξηγήσετε πιο καθαρά, σκεφτείτε μερικά από τα χαρακτηριστικά της φόρμας. Δηλαδή: η φόρμα είναι κάτι ολόκληρο, αλλά το σύνολο, με τη σειρά του, αποτελείται πάντα από μερικά μέρη. Αυτά τα μέρη είναι πιθανό να έχουν διαφορετικά χαρακτηριστικά, τουλάχιστον διαφορετικά μεγέθη. Λοιπόν, τέτοιες διαστάσεις είναι πάντα σε μια συγκεκριμένη αναλογία, τόσο μεταξύ τους όσο και σε σχέση με το σύνολο.

Επομένως, με άλλα λόγια, μπορούμε να το υποστηρίξουμεη χρυσή αναλογία είναι η αναλογία δύο ποσοτήτων, η οποία έχει τη δική της φόρμουλα. Η χρήση αυτής της αναλογίας κατά τη δημιουργία ενός σχήματος βοηθά να το κάνει όσο το δυνατόν πιο όμορφο και αρμονικό για το ανθρώπινο μάτι.
Η χρυσή αναλογία χρησιμοποιείται συχνά σεπολύ διαφορετικές σφαίρες της ζωής σήμερα. Αλλά η ιστορία αυτής της έννοιας ανάγεται στην αρχαιότητα, όταν μόλις εμφανίστηκαν επιστήμες όπως τα μαθηματικά και η φιλοσοφία. Ως επιστημονική ιδέα, η χρυσή αναλογία τέθηκε σε χρήση κατά την εποχή του Πυθαγόρα, δηλαδή τον 6ο αιώνα π.Χ. Αλλά ακόμη και πριν από αυτό, η γνώση μιας τέτοιας αναλογίας χρησιμοποιήθηκε στην πράξη στην Αρχαία Αίγυπτο και τη Βαβυλώνα. Μια ζωντανή απόδειξη αυτού είναι οι πυραμίδες, για την κατασκευή των οποίων χρησιμοποιήθηκε ακριβώς μια τέτοια χρυσή αναλογία.
Η Αναγέννηση έχει γίνει μια νέα ανάσα γιααρμονική διαίρεση, ειδικά χάρη στον Leonardo da Vinci. Αυτή η αναλογία άρχισε να χρησιμοποιείται όλο και περισσότερο τόσο στις ακριβείς επιστήμες, όπως η γεωμετρία, όσο και στην τέχνη. Επιστήμονες και καλλιτέχνες άρχισαν να μελετούν βαθύτερα τη χρυσή αναλογία και να δημιουργούν βιβλία που αντιμετωπίζουν αυτό το ζήτημα.
Ένα από τα πιο σημαντικά ιστορικά έργα,που σχετίζεται με τη χρυσή αναλογία είναι ένα βιβλίο της Luca Pancholi με τίτλο "Divine Proportion". Οι ιστορικοί υποψιάζονται ότι οι εικόνες σε αυτό το βιβλίο έγιναν από τον ίδιο τον Λεονάρντο πριν από τον Βίντσι.
Τα μαθηματικά δίνουν έναν πολύ σαφή ορισμόαναλογία, που δείχνει ότι είναι η ισότητα δύο αναλογιών. Μαθηματικά, αυτό μπορεί να εκφραστεί με την ακόλουθη ισότητα: a: b = c: d, όπου a, b, c, d είναι ορισμένες συγκεκριμένες τιμές.

Εάν εξετάσουμε την αναλογία ενός τμήματος που χωρίζεται σε δύο μέρη, τότε μπορούμε να αντιμετωπίσουμε μόνο μερικές καταστάσεις:
Όσον αφορά τη χρυσή αναλογία, αυτό είναιαναλογική διαίρεση του τμήματος σε άνισα μέρη, όταν ολόκληρο το τμήμα ανήκει στο μεγαλύτερο μέρος, καθώς και το ίδιο το μεγαλύτερο μέρος ανήκει στο μικρότερο. Υπάρχει μια άλλη διατύπωση: το μικρότερο τμήμα αναφέρεται στο μεγαλύτερο καθώς και το μεγαλύτερο σε ολόκληρο το τμήμα. Σε μαθηματικούς όρους, μοιάζει με αυτό: a: b = b: c ή c: b = b: a. Αυτή είναι η μορφή του τύπου χρυσού λόγου.
Η χρυσή αναλογία, παραδείγματα των οποίων είμαστε τώρασκεφτείτε, αναφέρεται σε απίστευτα φαινόμενα στη φύση. Αυτά είναι πολύ όμορφα παραδείγματα του γεγονότος ότι τα μαθηματικά δεν είναι απλώς αριθμοί και τύποι, αλλά η επιστήμη, η οποία έχει κάτι περισσότερο από έναν πραγματικό προβληματισμό στη φύση και τη ζωή μας γενικά.

Για τους ζωντανούς οργανισμούς, μια από τις βασικές ζωέςτα καθήκοντα είναι ανάπτυξη. Αυτή η επιθυμία να πάρει τη θέση της στο διάστημα, στην πραγματικότητα, πραγματοποιείται με διάφορες μορφές - ανοδική ανάπτυξη, σχεδόν οριζόντια απλώνεται κατά μήκος του εδάφους ή στρίβεται σε μια σπείρα σε μια συγκεκριμένη στήριξη. Και όσο απίστευτο μπορεί να είναι, πολλά φυτά αναπτύσσονται σύμφωνα με τη χρυσή αναλογία.
Ένα άλλο σχεδόν απίστευτο γεγονός είναι οι λόγοιστο σώμα των σαυρών. Το σώμα τους φαίνεται αρκετά ευχάριστο στο ανθρώπινο μάτι, και αυτό είναι δυνατό χάρη στην ίδια χρυσή αναλογία. Για να είμαστε πιο ακριβείς, το μήκος της ουράς τους αναφέρεται στο μήκος ολόκληρου του σώματος ως 62: 38.
Η χρυσή αναλογία είναι μια πραγματικά απίστευτη ιδέα, που σημαίνει ότι σε όλη την ιστορία μπορούμε να βρούμε πολλά πραγματικά ενδιαφέροντα γεγονότα σχετικά με μια τέτοια αναλογία. Εδώ είναι μερικά από αυτά:

Αυτή η ενότητα πρέπει να αναφέρει ένα πολύ σημαντικόάτομο, δηλαδή - S. Zeising. Πρόκειται για έναν Γερμανό ερευνητή που έχει κάνει τεράστια δουλειά στη μελέτη της χρυσής αναλογίας. Δημοσίευσε ένα έργο με τίτλο "Αισθητική Έρευνα". Στο έργο του, παρουσίασε τη χρυσή αναλογία ως απόλυτη έννοια που είναι καθολική για όλα τα φαινόμενα, τόσο στη φύση όσο και στην τέχνη. Εδώ μπορείτε να θυμηθείτε τη χρυσή αναλογία της πυραμίδας μαζί με την αρμονική αναλογία του ανθρώπινου σώματος και ούτω καθεξής.
Ήταν ο Zeising που κατάφερε να αποδείξει αυτό το χρυσόΗ διατομή είναι στην πραγματικότητα ο μέσος στατιστικός νόμος για το ανθρώπινο σώμα. Αυτό αποδείχθηκε στην πράξη, γιατί κατά τη διάρκεια της εργασίας του έπρεπε να μετρήσει πολλά ανθρώπινα σώματα. Οι ιστορικοί πιστεύουν ότι περισσότεροι από δύο χιλιάδες άνθρωποι συμμετείχαν σε αυτήν την εμπειρία. Σύμφωνα με την έρευνα του Zeising, ο κύριος δείκτης της χρυσής αναλογίας είναι η διαίρεση του σώματος από το σημείο του ομφαλού. Έτσι, το ανδρικό σώμα με μέσο λόγο 13: 8 είναι ελαφρώς πιο κοντά στον χρυσό λόγο από το γυναικείο σώμα, όπου ο χρυσός λόγος είναι 8: 5. Επίσης, η χρυσή αναλογία μπορεί να παρατηρηθεί σε άλλα μέρη του σώματος, όπως, για παράδειγμα, το χέρι.
Στην πραγματικότητα, η κατασκευή του χρυσού λόγου είναι θέμααπλός. Όπως μπορούμε να δούμε, ακόμη και οι αρχαίοι άνθρωποι το αντιμετώπισαν πολύ εύκολα. Τι μπορούμε να πούμε για τις σύγχρονες γνώσεις και τεχνολογίες της ανθρωπότητας. Σε αυτό το άρθρο, δεν θα δείξουμε πώς αυτό μπορεί να γίνει απλά σε ένα κομμάτι χαρτί και με ένα μολύβι στο χέρι, αλλά λέμε με σιγουριά ότι αυτό είναι πραγματικά δυνατό. Επιπλέον, αυτό μπορεί να γίνει με περισσότερους από έναν τρόπους.
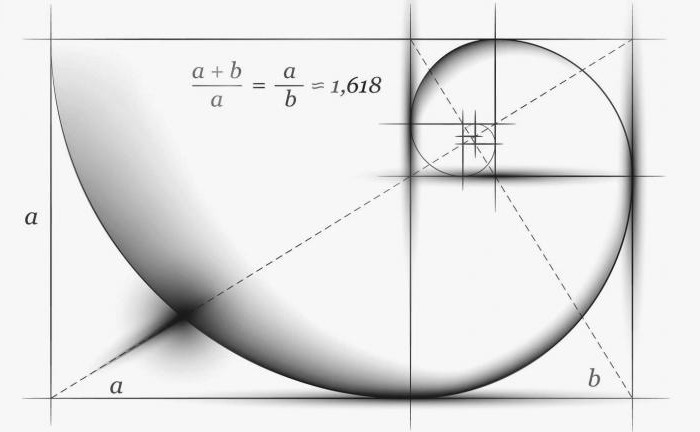
Δεδομένου ότι αυτή είναι μια αρκετά απλή γεωμετρία,η χρυσή αναλογία είναι αρκετά εύκολη στην κατασκευή ακόμη και στο σχολείο. Επομένως, πληροφορίες σχετικά με αυτό μπορούν εύκολα να βρεθούν σε εξειδικευμένα βιβλία. Μελετώντας τη χρυσή αναλογία, ο βαθμός 6 είναι πλήρως σε θέση να κατανοήσει τις αρχές της κατασκευής του, πράγμα που σημαίνει ότι ακόμη και τα παιδιά είναι αρκετά έξυπνα για να καταλάβουν ένα τέτοιο έργο.
Η πρώτη γνωριμία με τη χρυσή αναλογία στην πράξη ξεκινά με μια απλή διαίρεση ενός τμήματος ευθείας γραμμής, όλα με τις ίδιες αναλογίες. Τις περισσότερες φορές αυτό γίνεται με χάρακα, πυξίδα και, φυσικά, με μολύβι.
Τα τμήματα του χρυσού λόγου εκφράζονται ωςάπειρο παράλογο κλάσμα AE = 0,618 ..., εάν το AB λαμβάνεται ως μονάδα, BE = 0,382 ... Για να γίνει αυτός ο υπολογισμός πιο πρακτικός, δεν είναι ακριβής, αλλά χρησιμοποιούνται κατά προσέγγιση τιμές, δηλαδή - 0,62 και 0 38. Εάν το τμήμα AB λαμβάνεται ως 100 μέρη, τότε το μεγαλύτερο μέρος του θα είναι ίσο με 62, αλλά το μικρότερο θα είναι 38 μέρη, αντίστοιχα.

Η κύρια ιδιότητα του χρυσού λόγου μπορεί να εκφραστεί με την εξίσωση: x2-x-1 = 0. Κατά την επίλυση, έχουμε τις ακόλουθες ρίζες: x1,2=. Αν και τα μαθηματικά είναι μια ακριβής και αυστηρή επιστήμη, όπως το τμήμα της - γεωμετρία, αλλά είναι ακριβώς τέτοιες ιδιότητες όπως οι νόμοι της χρυσής αναλογίας που φέρνουν μυστήριο σε αυτό το θέμα.
Για να συνοψίσουμε, σκεφτείτε εν συντομία τι έχει ήδη ειπωθεί.
Κυρίως υπό τον κανόνα της χρυσής αναλογίαςΥπάρχουν πολλά παραδείγματα τέχνης, όπου η αναλογία είναι κοντά στα 3/8 και 5/8. Αυτή είναι η πρόχειρη φόρμουλα για τη χρυσή αναλογία. Το άρθρο έχει ήδη αναφέρει πολλά για παραδείγματα χρήσης της ενότητας, αλλά θα το εξετάσουμε ξανά μέσω του πρίσματος της αρχαίας και της σύγχρονης τέχνης. Έτσι, τα πιο εντυπωσιακά παραδείγματα από την αρχαιότητα:

Όσο για τους ήδη πιθανώς συνειδητούςΗ χρήση της αναλογίας, λοιπόν, ξεκινώντας από την εποχή του Λεονάρντο ντα Βίντσι, τέθηκε σε χρήση σε σχεδόν όλους τους κλάδους της ζωής - από την επιστήμη έως την τέχνη. Ακόμη και η βιολογία και η ιατρική έχουν αποδείξει ότι η χρυσή αναλογία λειτουργεί ακόμη και σε ζωντανά συστήματα και οργανισμούς.


























