
Prosessien tutkimus tilastollisessa muodossajärjestelmät, jotka ovat monimutkaisia pienimmän hiukkaskoon ja niiden valtavan määrän perusteella. On käytännössä mahdotonta tarkastella kutakin hiukkasta erikseen, siksi otetaan käyttöön tilastolliset suureet: hiukkasten keskimääräinen nopeus, niiden pitoisuus ja hiukkasten massa. Kaavaa, joka kuvaa järjestelmän tilaa ottaen huomioon mikroskooppiset parametrit, kutsutaan kaasujen molekyylikineettisen teorian (MKT) perusyhtälöksi.
Hiukkasten nopeuden määrittäminen suoritettiin ensinsuoritettiin kokeellisesti. Otto Sternin johtamasta kouluopetuksesta saatu kokemus antoi meille mahdollisuuden luoda idea hiukkasten nopeuksista. Kokeen aikana tutkittiin hopeatomien liikettä pyörivissä sylintereissä: ensin laitteen liikkumattomassa tilassa, sitten kun sitä pyöritetään tietyllä kulmanopeudella.
Tuloksena todettiin, että molekyylien nopeushopea ylittää äänen nopeuden arvon ja on 500 m / s. Tosiasia on melko mielenkiintoinen, koska ihmisen on vaikea tuntea tällaista aineiden hiukkasten nopeutta.
Продолжить исследование представляется возможным vain järjestelmässä, jonka parametrit voidaan määrittää suorilla mittauksilla fyysisiä laitteita käyttämällä. Nopeus mitataan nopeusmittarilla, mutta ajatus kiinnittää nopeusmittari erilliseen hiukkasiin on järjetöntä. Vain hiukkasten liikkeeseen liittyvä makroskooppinen parametri voidaan mitata suoraan.
Mikä tahansa vuorovaikutuksessa olevien elinten järjestelmäjolle on ominaista potentiaalienergia ja liikkeen kineettinen energia. Oikea kaasu on monimutkainen järjestelmä. Potentiaalienergian vaihtelua ei voida systemaatisoida. Ongelma voidaan ratkaista ottamalla käyttöön malli, jolla on kaasun ominaispiirteet huomioiden vuorovaikutuksen monimutkaisuus.
Ihanteellinen kaasu on aineen tila, jossahiukkasten vuorovaikutus on merkityksetöntä, vuorovaikutuksen potentiaalinen energia taipuu nollaan. Merkittävänä voidaan pitää vain liikkeen energiaa hiukkasten nopeudesta riippuen.

Tunnista kaasun paineen ja nopeuden välinen suhdesen hiukkasten liike sallii MKT-ihantekaasun perusyhtälön. Astiassa liikkuva hiukkanen, kun se osuu seinään, antaa sille impulssin, jonka arvo voidaan määrittää Newtonin lain II perusteella:
Hiukkasen liikemäärän muutos elastisen iskun aikana liittyy muutokseen sen nopeuden vaakakomponentissa. F on voima, joka vaikuttaa seinämään hiukkasesta lyhyeksi ajaksi t; m0 - hiukkasten massa.
Kaikki kaasupartikkelit, jotka liikkuvat pinnan suunnassa nopeudella vkanssa ja se sijaitsee Sυ-tilavuuden sylinterissäkanssaΔt. Kun hiukkasten pitoisuus on n, tarkalleen puolet molekyyleistä liikkuu seinää kohti, toinen puoli vastakkaiseen suuntaan.
Harkittuaan kaikkien hiukkasten törmäyksen voimme kirjoittaa Newtonin lain paikalle vaikuttavalle voimalle:
Koska kaasun paine määritellään pintaan kohtisuoraan vaikuttavan voiman suhteena jälkimmäisen pinta-alaan, voimme kirjoittaa:
Tuloksena oleva suhde MKT: n perusyhtälönä ei voi kuvata koko järjestelmää, koska otetaan huomioon vain liike yhteen suuntaan.
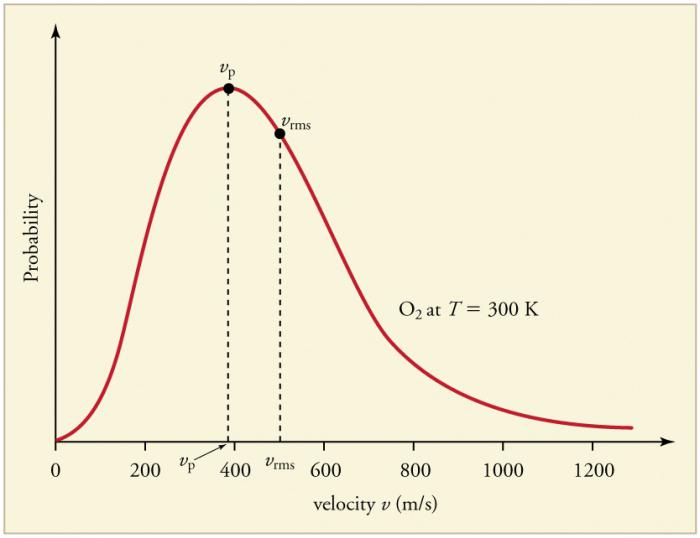
Kaasupartikkelien jatkuvat toistuvat törmäyksetseinät ja johtavat toistensa kanssa tietyn hiukkasten tilastollisen jakauman muodostumiseen nopeuksien (energioiden) mukaan. Kaikkien nopeusvektorien suunnat ovat yhtä todennäköiset. Tätä jakaumaa kutsutaan Maxwell-jakaumaksi. Vuonna 1860 J. Maxwell päätti tämän mallin MKT: n perusteella. Jakelulain pääparametreja kutsutaan nopeuksiksi: todennäköiset, jotka vastaavat käyrän maksimiarvoa, ja rms vm². = √ ‹v2›- hiukkasten nopeuden keskimääräinen neliö.
Kaasun lämpötilan nousu vastaa nopeusarvon nousua.
Perustuen siihen, että kaikki nopeudet ovat samat ja niiden moduuleilla on sama arvo, voimme harkita:
MKT: n perusyhtälö, ottaen huomioon kaasun paineen keskiarvo, on muoto:
Tämä suhde on ainutlaatuinen siinä mielessä, että se määrittää mikroskooppisten parametrien välisen suhteen: nopeuden, hiukkasten massan, hiukkasten pitoisuuden ja yleensä kaasun paineen.
Käyttämällä hiukkasten kineettisen energian käsitettä MKT: n perusyhtälö voidaan kirjoittaa uudestaan:
Kaasun paine on verrannollinen hiukkasten keskimääräiseen kineettiseen energiaan.
On mielenkiintoista, että tasaisella kaasumäärälläsuljettu astia, voit verrata kaasun painetta ja hiukkasten liikkeen energian keskiarvoa. Tässä tapauksessa paineen mittaus voidaan suorittaa mittaamalla hiukkasten energia.
Kuinka edetä? Mitä määrää voidaan verrata kineettiseen energiaan? Tämä arvo osoittautuu lämpötilaksi.


Mielenkiintoisempi riippumattomuuskäyttönesteen ominaisuuksia voidaan pitää kaasulämpömittareina. Niiden asteikko on riippumaton käytetystä kaasutyypistä. Tällaisessa laitteessa voidaan hypoteettisesti valita lämpötila, jossa kaasun paine pyrkii nollaan. Laskelmat osoittavat, että tämä arvo vastaa arvoa -273,15 noinAlkaen.Lämpötila-asteikko (absoluuttinen lämpötila-asteikko tai Kelvin-asteikko) otettiin käyttöön vuonna 1848. Mahdollinen nollakaasun paineen lämpötila otettiin tämän asteikon pääpisteeksi. Asteikon yksikköosuus on yhtä suuri kuin Celsius-asteikon yksikköarvo. MKT: n perusyhtälö on helpompi kirjoittaa lämpötilaa käyttäen kaasuprosesseja tutkittaessa.
Empiirisesti voit varmistaa, että kaasun paine on verrannollinen sen lämpötilaan. Samanaikaisesti todettiin, että paine on suoraan verrannollinen hiukkasten pitoisuuteen:
missä Т on absoluuttinen lämpötila, k on vakioarvo, joka on 1,38 • 10-23J / K.
Perusmäärää, jolla on vakio arvo kaikille kaasuille, kutsutaan Boltzmannin vakiona.
Vertaamalla paineen riippuvuutta lämpötilasta ja MKT-kaasujen perusyhtälöä, voit kirjoittaa:
Kaasumolekyylien liike-energian keskiarvo on verrannollinen sen lämpötilaan. Toisin sanoen lämpötila voi toimia hiukkasliikkeen kineettisen energian mittana.


























