
Kolmio on yksi yleisimmistägeometriset muodot, jotka opimme tuntemaan jo ala-asteella. Jokainen geometrialuokkien opiskelija kohtaa kysymyksen siitä, kuinka löytää kolmion pinta-ala. Joten mitä piirteitä tietyn hahmon alueen löytämiselle voidaan erottaa? Tässä artikkelissa tarkastellaan tämän tehtävän suorittamiseen tarvittavia peruskaavoja ja analysoidaan myös kolmiotyyppejä.

Löydät kolmion pinta-alan täysin eri tavoin, koska geometriassa erottuu useampi kuin yksi kuva, joka sisältää kolme kulmaa. Näihin tyyppeihin kuuluvat:
Tarkastellaan yksityiskohtaisemmin kaikkia olemassa olevia kolmioita.

Tällaista geometrista kuvaa pidetään enitenyleinen ratkaistaessa geometrisiä ongelmia. Kun on tarpeen piirtää mielivaltainen kolmio, tämä vaihtoehto tulee auttamaan.
Kuten nimestä käy ilmi, teräväkulmaisessa kolmiossa, kaikki kulmat ovat teräviä ja lisäävät jopa 180 °.
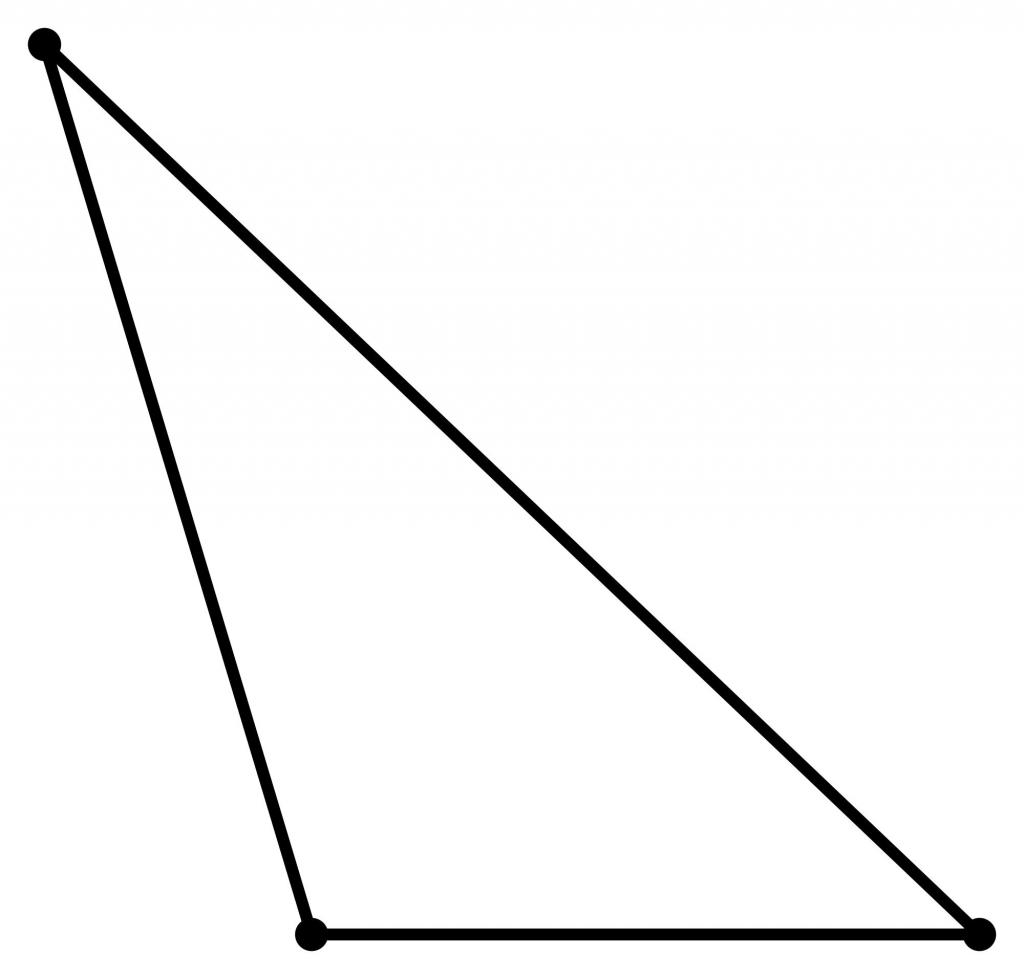
Tällainen kolmio on myös hyvin yleinen,se on kuitenkin jonkin verran harvempaa kuin akuutin kulman. Esimerkiksi ratkaistaessa kolmioita (ts. Useita sen sivuja ja kulmia tunnetaan ja jäljelle jäävät elementit on löydettävä), joskus on tarpeen selvittää, onko kulma tylppä vai ei. Kaltevuuskulman kosini on negatiivinen luku.
Häiriöttömässä kolmiossa yhden kulman arvo ylittää 90 °, joten loput kaksi kulmaa voivat ottaa pieniä arvoja (esimerkiksi 15 ° tai jopa 3 °).
Tämän tyyppisen kolmion alueen löytämiseksi sinun on tiedettävä joitain vivahteista, joista puhumme myöhemmin.
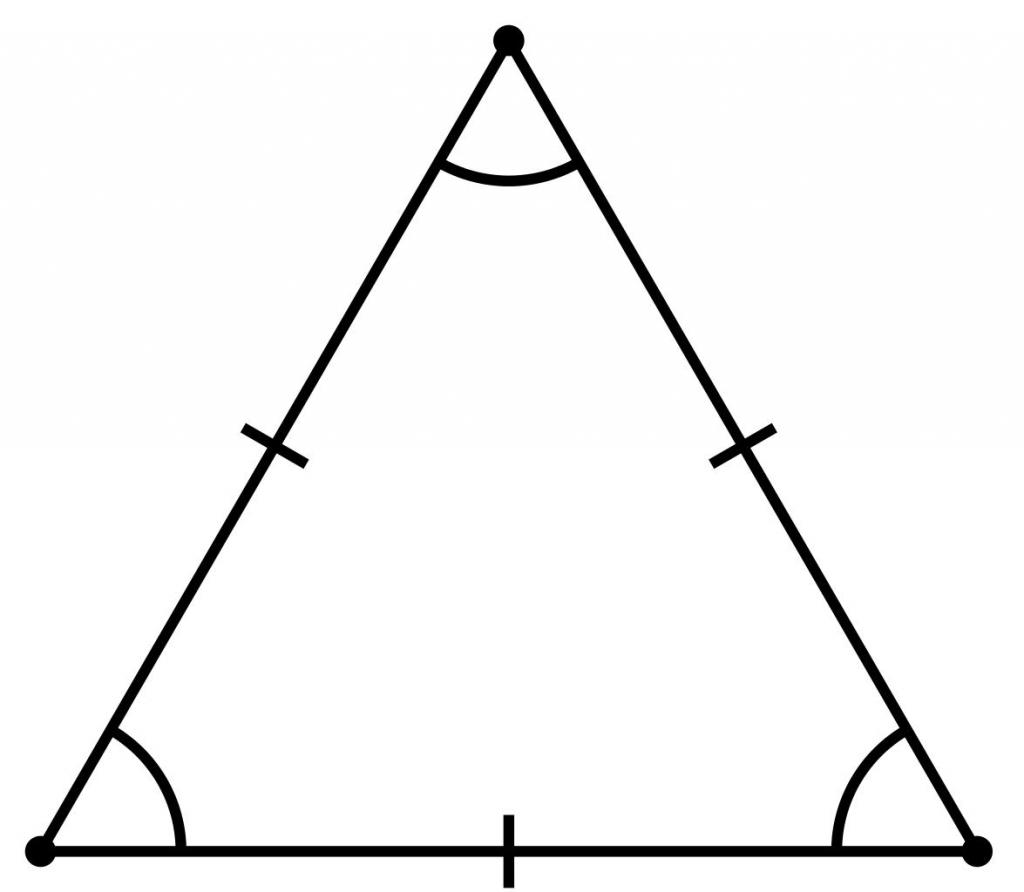
Säännöllinen monikulmio on muoto,mukaan lukien n kulma, jossa kaikki sivut ja kulmat ovat yhtä suuret. Se on säännöllinen kolmio. Koska kolmion kaikkien kulmien summa on 180 °, niin jokainen kolmesta kulmasta on 60 °.
Säännöllistä kolmiota, ominaisuutensa vuoksi, kutsutaan myös tasasivuiseksi lukuksi.
On myös syytä huomata, että normaaliin kolmioon voidaan kirjoittaa vain yksi ympyrä ja sen ympärille voidaan kuvata vain yksi ympyrä ja niiden keskipisteet sijaitsevat yhdessä pisteessä.

Tasasivuisen tyypin lisäksi voimme erottaa myös toisistaantasakulmainen kolmio, hiukan erilainen siitä. Tällaisessa kolmiossa kaksi puolta ja kaksi kulmaa ovat keskenään yhtä suuret, ja kolmas puoli (jonka kanssa yhtä suuret kulmat ovat vierekkäin) on pohja.
Kuvassa on tasakulmainen kolmio DEF, jonka kulmat D ja F ovat yhtä suuret ja DF on perusta.

Suorakulmainen kolmio on niin kutsuttu, koska yksi sen kulmista on suora, ts. 90 °. Kaksi muuta kulmaa lisäävät jopa 90 °.
Tällaisen kolmion suurin puoli, joka on 90 ° kulmaa vasten, on hypotenuse, kun taas kaksi muuta puolta ovat jalkoja. Tämän tyyppisille kolmioille voidaan soveltaa Pythagoran lausetta:
Jalkojen neliöpituuksien summa on yhtä suuri kuin hypotenuksen neliöpituus.
Kuvassa on esitetty suorakulmainen kolmio BAC hypotenuusiilla AC ja jaloilla AB ja BC.
Suorakulmaisen kolmion alueen löytämiseksi sinun on tiedettävä sen jalkojen numeeriset arvot.
Otamme kaavoja tämän kuvan alueen löytämiseksi.
Geometriassa on kaksi kaavaasopii useimpien kolmiotyyppien, nimittäin akuutti-, tylppä-, säännöllisten ja tasakulmaisten kolmioiden, löytämiseen. Analysoimme kutakin niistä.
Tämä kaava on universaalilöytää luku, jota me pidämme. Tämän tekemiseksi riittää, että tiedät sivun pituuden ja siihen vetettyn korkeuden pituuden. Itse kaava (puolet pohjan korkeudesta) on seuraava:
S = ½ * A * H,
missä A on annetun kolmion sivu ja H on kolmion korkeus.

Esimerkiksi, kun haluat löytää akuutin kulman kolmion ACB alueen, sinun täytyy kertoa sen sivu AB korkeudella CD ja jakaa saatu arvo kahdella.
Alueen löytäminen ei kuitenkaan ole aina helppoa.kolmio tällä tavalla. Esimerkiksi, jotta tätä kaavaa voitaisiin käyttää synkkään kolmioon, sinun on jatkettava yhtä sen sivua ja vasta sen jälkeen piirrä siihen korkeus.
Käytännössä tätä kaavaa käytetään useammin kuin toisia.
Tämä kaava, kuten edellinen, sopiiUseimmat kolmiot ja niiden merkityksessä ovat seurausta kaavasta, jolla löydetään alue kolmion sivua ja korkeutta pitkin. Eli harkittu kaava voidaan helposti johtaa edellisestä. Sen sanamuoto näyttää tältä:
S = ½ * sinO * A * B,
missä A ja B ovat kolmion sivut ja O on kulma A: n ja B: n välillä.
Muista, että kulman sini löytyy erityisestä taulukosta, joka on nimetty erinomaisen Neuvostoliiton matemaatikon V. M. Bradiksen mukaan.
Siirrytään nyt muihin kaavoihin, jotka soveltuvat vain poikkeuksellisille kolmiotyypeille.
Yleismaailmallisen kaavan lisäksi, johon sisältyy tarve piirtää korkeus kolmioon, jalat löytävät suorakulmaisen kolmion pinnan.
Joten suorakulmaisen kolmion pinta-ala on puolet jalkojensa tuloksesta, tai:
S = ½ * a * b,
missä a ja b ovat suorakulmaisen kolmion jalat.
Tämäntyyppiset geometriset muodot eroavat siinäettä sen pinta-ala löytyy vain yhden sivun osoitetulla arvolla (koska säännöllisen kolmion kaikki sivut ovat yhtä suuret). Joten suoritettuaan tehtävän "löytää kolmion pinta-ala, kun sivut ovat samat", sinun on käytettävä seuraavaa kaavaa:
S = a2* √3 / 4,
missä A on tasasivuisen kolmion sivu.
Viimeinen vaihtoehto kolmion pinta-alan löytämiseksi on Heron-kaava. Jotta sitä voidaan käyttää, sinun on tiedettävä kuvan kolmen sivun pituudet. Heronin kaava näyttää tältä:
S = √p · (p - a) · (p - b) · (p - c),
missä a, b ja c ovat annetun kolmion sivut.
Joskus tehtävässä se annetaan:"Säännöllisen kolmion pinta-ala on löytää sen sivun pituus." Tässä tapauksessa meidän on käytettävä jo tunnettua kaavaa säännöllisen kolmion pinnan löytämiseksi ja johdettava siitä sivun (tai sen neliön) arvo:
A2 4S/Z3.
Vuonna GIA tehtäviä matematiikassa on monia kaavoja.
Tässä tapa uksessa on kätevämpää pitää korkeus kuvion toisella puolella, määrittää solujen pituus ja käyttää universaalia kaavaa löytääksesi alueen:
S q 1/2 ' A'H.
Joten, tutkittuaan kaavoja, jotka on esitetty artikkelissa, sinun ei tarvitseongelmia löytää alueen minkäänlaista kolmion.


























