
संबंधों की एक विस्तृत श्रृंखला सेट के रूप में अनुकरणीय हैबड़ी संख्या में अवधारणाओं के साथ, उनकी परिभाषाओं से शुरू होकर विरोधाभासों के विश्लेषणात्मक विश्लेषण के साथ समाप्त होता है। सेट पर लेख में चर्चा की गई अवधारणा की विविधता अनंत है। हालांकि, जब वे दोहरे प्रकारों के बारे में बात करते हैं, तो उनका मतलब कई मात्राओं के बीच द्विआधारी संबंध होता है। और वस्तुओं या कथनों के बीच भी।
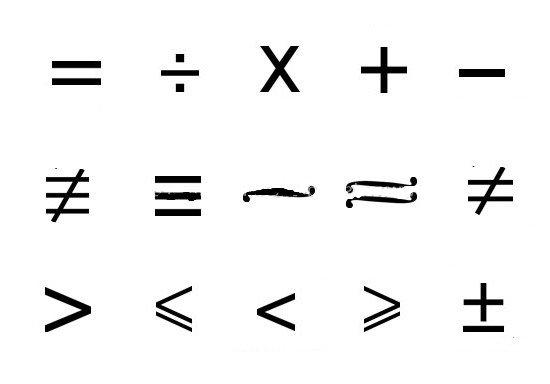
आमतौर पर, द्विआधारी रिश्तों को निरूपित किया जाता हैप्रतीक R, अर्थात, यदि फ़ील्ड R से किसी भी मान x के लिए xRx, ऐसी संपत्ति को रिफ्लेक्सिव कहा जाता है, जिसमें x और x को विचार की ऑब्जेक्ट स्वीकार किया जाता है, और R व्यक्तियों के बीच एक या दूसरे प्रकार के संबंध का संकेत होता है। उसी समय, अगर हम xRy® या yRx को व्यक्त करते हैं, तो यह समरूपता की स्थिति को इंगित करता है, जहां ® एक संकेत है जो संयोजन के समान है "अगर ..., तो ..." और, अंत में, शिलालेख (xRy Ùy Rz) को डिकोड करना ®xRz आपको एक सकर्मक संबंध के बारे में बताएगा, और a चिन्ह एक संयोजन है।
एक द्विआधारी संबंध जो एक ही समय में होता हैप्रतिवर्त, सममित और सकर्मक, इसे एक समतुल्य संबंध कहा जाता है। संबंध f एक फ़ंक्शन है, और <x, y> <f और <x, z> it से यह निम्न है कि y = z। एक साधारण बाइनरी फ़ंक्शन को एक निश्चित क्रम में दो सरल तर्कों पर आसानी से लागू किया जा सकता है, और केवल इस मामले में यह इन दो भावों को निर्देशित अर्थ प्रदान करता है, किसी विशेष मामले में लिया जाता है।
यह कहा जाना चाहिए कि f मैप्स x to y,

उपरोक्त के आधार पर, द्विआधारी संबंधों के तुलनीय संबंध गुणों द्वारा निर्धारित किए जाते हैं:
बाइनरी संबंधों के घोषित गुणों पर विचार करेंविस्तृत रूप में। रिफ्लेक्सिटी कुछ कनेक्शनों की विशेषताओं में से एक है, जहां जांच किए गए सेट का प्रत्येक तत्व खुद को दिए गए समानता में है। उदाहरण के लिए, संख्याओं के बीच a = c और a ref c रिफ्लेक्टिव कनेक्शन हैं, क्योंकि हमेशा a = a, c = c, a numbers a, c³ c। इसी समय, असमानता संबंध ए> सी असमानता के अस्तित्व की असंगति के कारण एंटीरेफ्लेक्सिव है ए> ए। इस संपत्ति का स्वयंसिद्ध संकेत द्वारा एन्कोड किया गया है: aRc® aRa om cRc, यहाँ पर प्रतीक® का अर्थ है "एंट्रेस" (या "तात्पर्य"), और संकेत Ù संघ है "और" (या संयोजन) "। यह इस कथन का अनुसरण करता है कि यदि निर्णय aRc सत्य है, तो aRa और cRc भाव भी सत्य हैं।

समरूपता एक रिश्ते को मजबूर करती हैऔर इस घटना में कि मानसिक वस्तुएं परस्पर जुड़ी होती हैं, अर्थात, एक सममित संबंध के साथ, वस्तुओं की क्रमबद्धता "बाइनरी संबंधों" के रूप में परिणत नहीं होती है। उदाहरण के लिए, समानता का संबंध a = c सममितीय है क्योंकि संबंध c = a; निर्णय aondsc भी वही है, क्योंकि यह कनेक्शन के साथ मेल खाता है।
एक सकर्मक सेट एक ऐसी संपत्ति है, जिसके लिएजो निम्न आवश्यकता को पूरा करता है: y, x, z z y® z where x, जहाँ ® शब्दों की जगह एक संकेत है: "अगर ..., तो ..."। सूत्र को मौखिक रूप से इस प्रकार पढ़ा जाता है: "यदि y x पर निर्भर करता है, तो z, y से संबंधित है, तो z भी x पर निर्भर करता है।"


























