
Matematičke zagonetke su nezamisliveiznos. Svaki od njih je jedinstven na svoj način, ali njihov šarm leži u činjenici da se za njegovo rješavanje neizbježno mora doći do formula. Naravno, možete ih pokušati riješiti, kako kažu, nasumce, ali to će biti jako dugo i gotovo neuspješno.
Ovaj članak će govoriti o jednom odtakve tajne, točnije - o magičnom trgu. Detaljno ćemo analizirati kako riješiti čarobni trg. Razred 3 općeg obrazovnog programa, naravno, prolazi, ali možda nisu svi razumjeli ili se uopće ne sjećaju.
Magicni kvadrat, ili, kako se zove,magic, je tablica u kojoj je broj stupaca i redaka isti, a svi su popunjeni različitim brojevima. Glavni zadatak je da ove brojke u visini okomite, horizontalne i dijagonalne daju istu vrijednost.
Osim čarobnog trga, tu je takođersemimagic. To znači da je zbroj brojeva isti samo vertikalno i horizontalno. Čarobni kvadrat je "normalan" samo ako se za punjenje koriste prirodni brojevi.
Tu je i takva stvar kao simetrični magični kvadrat - to je kada je vrijednost zbroja dviju znamenki jednaka, dok su oni simetrično raspoređeni u odnosu na središte.
Također je važno znati da kvadrati mogu biti bilo koje veličine osim 2 na 2. Kvadrat od 1 po 1 također se smatra magičnim, budući da su svi uvjeti ispunjeni, iako se sastoji od jednog broja.
Dakle, s definicijom koju smo pročitali, sada ćemo govoriti o tome kako riješiti čarobni trg. 3. stupanj školskog kurikuluma vjerojatno neće sve objasniti tako detaljno kao ovaj članak.
Oni ljudi koji znaju riješiti magijukvadrat (pouzdano zna 3. klasa), odmah kažu da postoje samo tri rješenja, a svaka od njih je prikladna za različite kvadrate, ali ipak je nemoguće ignorirati četvrto rješenje, naime „nasumce“. Doista, u nekoj mjeri je vjerojatno da će osoba koja ne zna još uvijek moći riješiti taj problem. No, odbacit ćemo ovu metodu u dugačku kutiju i prijeći izravno na formule i metode.
Ova metoda je prikladna samo za rješavanje takvog kvadrata u kojem je broj stanica neparan, na primjer 3 prema 3 ili 5 sa 5.
Dakle, u svakom slučaju, u početku je potrebno pronaći magičnu konstantu. To je broj koji će se dobiti kada zbroj brojeva dijagonalno, vertikalno i horizontalno. Izračunava se pomoću formule:
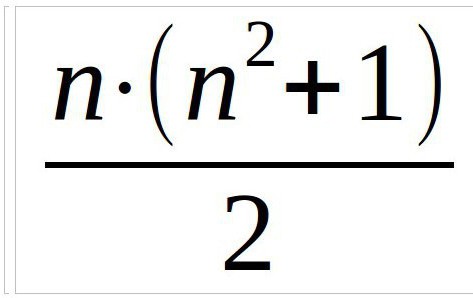
U ovom primjeru razmotrit ćemo kvadrat od tri po tri, tako da će formula izgledati ovako (n je broj stupaca):
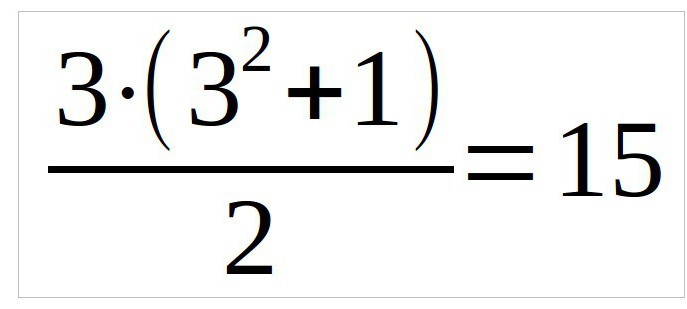
Dakle, imamo kvadrat. Prvo što trebate učiniti jest unijeti broj jedan u središte prvog retka na vrhu. Sve slijedeće slike moraju biti postavljene na jedno mjesto na desnoj dijagonali.
Ali onda se odmah postavlja pitanje kako riješiti magijukvadrat? 3. stupanj vjerojatno neće koristiti ovu metodu, a većina će imati problem, kako to učiniti na taj način ako ne postoji takva stanica? Da biste sve učinili kako valja, morate uključiti maštu i nacrtati sličan magični kvadrat na vrhu i ispada da će broj 2 biti u njemu u donjoj desnoj ćeliji. Dakle, na našem trgu ulazimo u dva na istom mjestu. To znači da moramo unijeti brojeve tako da ukupno daju vrijednost od 15.
Naknadni brojevi odgovaraju točno istom.To jest, 3 će biti u središtu prvog stupca. No, 4 na ovom principu neće moći ući, jer je na njegovom mjestu već jedinica. U ovom slučaju, broj 4 se nalazi ispod 3 i nastavlja se. Pet - u središtu trga, 6 - u gornjem desnom kutu, 7 - ispod 6, 8 - u gornjem lijevom i 9 - u sredini donjeg retka.
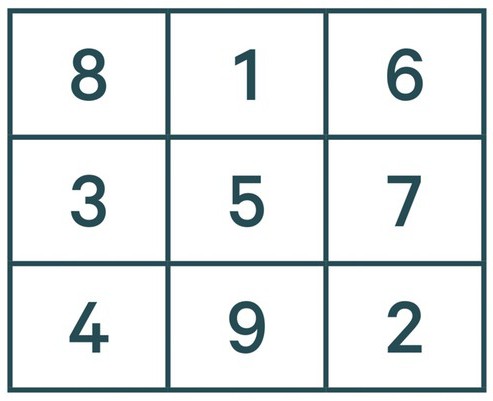
Sada znate kako riješiti čarobni trg.3. stupanj Demidov prošao, ali ovaj autor je nešto jednostavniji zadatak, međutim, znajući ovu metodu, bit će moguće riješiti bilo koji takav problem. Ali ako je broj stupaca neparan. I što učiniti ako, na primjer, imamo kvadrat 4? O tome dalje u tekstu.
Kvadrat dvostrukog pariteta je onaj u kojem se broj stupaca može podijeliti na 2 i 4. Sada ćemo uzeti kvadrat 4 za 4.
Dakle, kako riješiti čarobni kvadrat (razred 3, Demidov, Kozlov, Tonkikh - zadatak u udžbeniku matematike) kada je broj njegovih stupaca 4? Vrlo jednostavno. Lakše nego u prethodnom primjeru.
Prvo nalazimo magičnu konstantuista formula koja je citirana posljednji put. U ovom primjeru broj je 34. Sada morate poravnati brojeve tako da je zbroj vertikalne, horizontalne i dijagonalne jednak.
В первую очередь надо закрасить некоторые ячейки, to možete učiniti olovkom ili maštom. Obojite sve uglove, tj. Gornju lijevu i gornju desnu, donju lijevu i donju desnu stranu. Ako bi kvadratić bio 8 do 8, onda je potrebno naslikati ne jednu ćeliju u kutu, već četiri, 2 prema 2.
Sada je potrebno slikati preko središta tog kvadrata, tako da njegovi uglovi dodiruju uglove već oslikanih ćelija. U ovom primjeru dobivamo kvadrat u sredini od 2 po 2.
Početak rada.Napunit ćemo se s lijeva na desno, redoslijedom po kojem se stanice nalaze, samo ćemo unijeti vrijednost u ispunjene ćelije. Ispada da u gornjem lijevom kutu ulazimo 1, desno - 4. Zatim popunjavamo središnje 6, 7 i dalje 10, 11. Donji lijevi 13 i desni - 16. Smatramo da je redoslijed punjenja jasan.

Preostale stanice se popunjavaju na potpuno isti način, samo usilaznim redoslijedom. To jest, budući da je posljednja upisana figura bila 16, piše 15 na vrhu kvadrata, a zatim 14. Zatim 12, 9, i tako dalje, kao što je prikazano na slici.
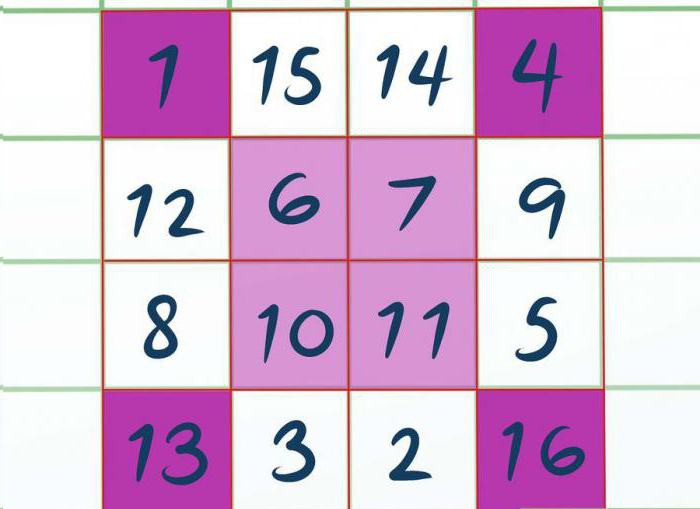
Sada znate drugi način kako riješiti čarobni trg. Stupanj 3 se slaže da su kvadrati s dvostrukim paritetom lakše riješiti nego drugi. Pa, idemo na posljednju metodu.
Kvadrat jednog pariteta naziva se taj kvadrat, čiji se broj stupaca može podijeliti na dva, ali ne na četiri. U ovom slučaju, to je kvadrat od 6 x 6.
Dakle, izračunavamo magičnu konstantu. Ona je jednaka 111.
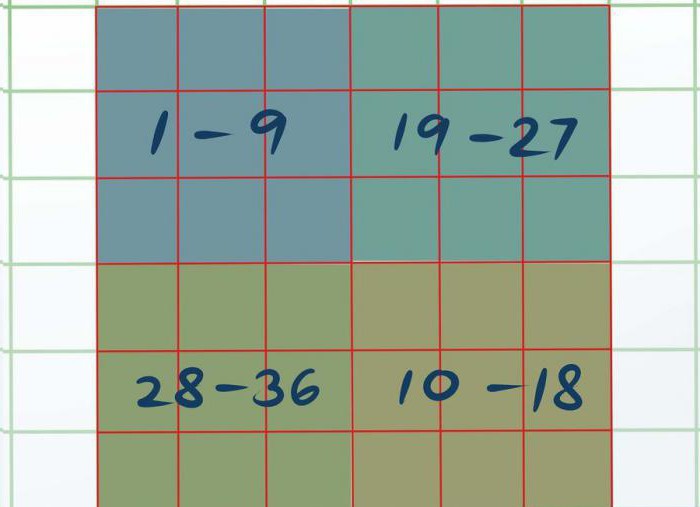
Sada moramo vizualno podijeliti naš trg načetiri različita kvadrata od 3 do 3. Bit će četiri mala kvadrata mjerena 3 po 3 u jednom velikom 6 na 6. Gornji lijevi se zove A, donji desni je B, gornji desni C je, a donji lijevi D.

Sada je svaki mali trg potrebanriješiti pomoću prve metode koja je dana u ovom članku. Ispostavlja se da će u kvadratu A biti brojki od 1 do 9, u B - od 10 do 18, u C - od 19 do 27 i D - od 28 do 36.
Nakon što ste riješili sva četiri kvadrata, raditeće početi iznad A i D. Potrebno je odabrati tri ćelije u kvadratu A vizualno ili s olovkom, naime: gornji lijevi, središnji i donji lijevi. Ispostavlja se da su označeni brojevi 8, 5 i 4. Na isti način treba istaknuti kvadrat D (35, 33, 31). Sve što preostaje je zamijeniti dodijeljene znamenke iz kvadrata D u A.
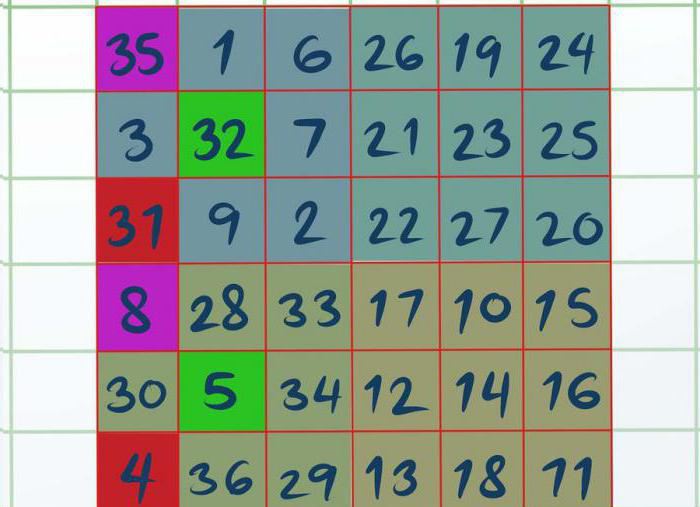
Sada znate posljednji način rješavanja magičnog trga. 3 klasa kvadratnih paritet ne voli najviše. I to ne čudi, od svih predstavljenih, to je najsloženije.
Nakon što ste pročitali ovaj članak, naučili ste kako ga riješitičarobni trg. 3. razred (Moro - autor udžbenika) nudi slične zadatke sa samo nekoliko ispunjenih stanica. To nema smisla uzeti u obzir njegove primjere, jer znajući sve tri metode, lako možete riješiti sve predložene probleme.


























