
בחלל, המטוס יכול להיות מוגדר על ידי שונהדרכים (נקודה אחת וקטור, שתי נקודות וקטור, שלוש נקודות וכו '). מתוך מחשבה על כך, למשוואת המטוס יכולות להיות צורות שונות. כמו כן, אם מתקיימים תנאים מסוימים, המטוסים יכולים להיות מקבילים, בניצב, מצטלבים וכו '. נדבר על כך במאמר זה. נלמד כיצד לנסח את המשוואה הכללית של המטוס ועוד.
נניח שיש רווח R3, בעלת מערכת קואורדינטות XYZ מלבנית. הבה נגדיר וקטור α, אשר ישוחרר מהנקודה ההתחלתית O. דרך קצה הווקטור α, צייר מישור P, שיהיה בניצב אליו.
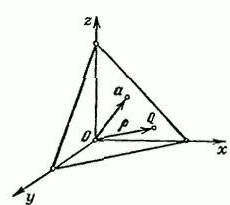
אנו מציינים בנקודה שרירותית Q = (x, y, z). הבה נחתום את וקטור הרדיוס של הנקודה Q באות p. במקרה זה, אורך הווקטור α שווה ל- p = IαI ו- Ʋ = (cosα, cosβ, cosγ).
זהו וקטור יחידה שמכוון אליוצד, כמו גם וקטור α. α, β ו- γ הן הזוויות הנוצרות בין הווקטור Ʋ והכיוונים החיוביים של צירי החלל x, y, z, בהתאמה. ההקרנה של כל נקודה QϵП על הווקטור Ʋ היא ערך קבוע, ששווה ל- p: (p, Ʋ) = p (p≥0).
המשוואה לעיל הגיונית כאשר p = 0.הדבר היחיד הוא שמישור P במקרה זה יחתוך את הנקודה O (α = 0), שהיא המקור, וקטור היחידה Ʋ הנפלט מנקודה O יהיה בניצב ל- P, למרות כיוונו, כלומר הווקטור Ʋ נקבע במדויק לסימן. המשוואה הקודמת היא משוואת המישור P שלנו, המתבטאת בצורה וקטורית. אך בקואורדינטות מראהו יהיה כך:

P כאן גדול או שווה ל 0. מצאנו את משוואת המטוס בחלל בצורה הרגילה.
אם המשוואה בקואורדינטות מוכפלת במספר שאינו אפס, נקבל משוואה המקבילה לזה הנתון, המגדיר את אותו המטוס. זה יראה כך:

כאן A, B, C הם מספרים שאינם אפס בו זמנית. משוואה זו מכונה משוואת המישור הכללי.
ניתן לשנות את המשוואה הכללית בנוכחות תנאים נוספים. בואו נסתכל על כמה מהם.
נניח שהמקדם A שווה ל- 0. המשמעות היא שמישור זה מקביל לציר Ox נתון. במקרה זה צורת המשוואה תשתנה: Vu + Cz + D = 0.
באופן דומה צורת המשוואה תשתנה בתנאים הבאים:
במקרה שבו המספרים A, B, C, D אינם אפס, צורת המשוואה (0) יכולה להיות כדלקמן:
x / a + y / b + z / c = 1,
שבו a = -D / A, b = -D / B, c = -D / C.
כתוצאה מכך, אנו מקבלים את משוואת המטוס במקטעים. ראוי לציין כי מטוס זה יחתוך את ציר השור בנקודה עם קואורדינטות (א, 0,0), אוי - (0, ב, 0) ואוז - (0,0, ג).

בהתחשב במשוואה x / a + y / b + z / c = 1, קל לייצג ויזואלית את מיקום המטוס ביחס למערכת קואורדינטות נתונה.
לווקטור הנורמלי n למישור P יש קואורדינטות שהם המקדמים של המשוואה הכללית של המטוס הזה, כלומר n (A, B, C).

על מנת לקבוע את הקואורדינטות של ה- n הרגיל, די לדעת את המשוואה הכללית של המטוס הנתון.
בעת שימוש במשוואת קטע קו זהבעל הטופס x / a + y / b + z / c = 1, כמו בעת השימוש במשוואה הכללית, אתה יכול לכתוב את הקואורדינטות של כל וקטור נורמלי של מישור נתון: (1 / a + 1 / b + 1 / c ).
ראוי לציין כי הווקטור הרגיל עוזרלפתור בעיות שונות. הבעיות הנפוצות ביותר כוללות את בעיית הוכחת הניצב או ההקבלה של המטוסים, בעיית מציאת הזוויות בין המישורים או הזוויות בין המטוסים לקווים.
וקטור n אפס n הניצב למישור נתון נקרא נורמלי (נורמלי) למישור נתון.
נניח שבחלל קואורדינטות (מערכת קואורדינטות מלבנית) ניתנים לאוקסיז:

יש צורך לערוך משוואה למישור שיעבור דרך הנקודה Mₒ בניצב ל- n הרגיל.
בחלל, בחר כל נקודה שרירותית ואנו מציינים אותו ב- M (xy, z). תנו לקטור הרדיוס של כל נקודה M (x, y, z) להיות r = x * i + y * j + z * k, וקטור הרדיוס של הנקודה Mₒ (xₒ, yₒ, zₒ) - rₒ = xₒ * i + yₒ * j + zₒ * k. הנקודה M תהיה שייכת למישור הנתון אם הווקטור МₒМ בניצב לווקטור n. הבה נכתוב את תנאי האורתוגונליות באמצעות מוצר הנקודה:
[MM, n] = 0.
מאחר МₒМ = r - rₒ, משוואת הווקטורים של המטוס תיראה כך:
[r - rₒ, n] = 0.
למשוואה זו יכולה להיות צורה אחרת.לשם כך משתמשים במאפיינים של מוצר הנקודה, והצד השמאלי של המשוואה משתנה. [r - rₒ, n] = [r, n] - [rₒ, n]. אם [rₒ, n] מסומן כ c, נקבל את המשוואה הבאה: [r, n] - c = 0 או [r, n] = c, המבטא את קביעות ההשלכות על הווקטור הרגיל של וקטורי הרדיוס של נתון נקודות השייכות למטוס.
כעת תוכל לקבל את צורת הקואורדינטות של כתיבת משוואת הווקטורים של המישור שלנו [r - rₒ, n] = 0. מאחר r - rₒ = (x - xₒ) * i + (y - yₒ) * j + (z - zₒ ) * k, ו- n = A * i + B * j + C * k, יש לנו:

מסתבר שיש לנו משוואה של מטוס העובר בנקודה בניצב ל- n הרגיל:
A * (x- xₒ) + B * (y– yₒ) C * (z- zₒ) = 0.
הבה נקבע שתי נקודות שרירותיות M '(x', y ', z') ו- M ″ (x ″, y ″, z ″), וכן וקטור a (a ′, a ″, a).
כעת נוכל לצייר משוואה של מישור נתון, שתעבור דרך הנקודות הקיימות M ′ ו- ″, כמו גם כל נקודה M עם קואורדינטות (x, y, z) במקביל לווקטור נתון a.
יתר על כן, הווקטורים M′M = {x -x ′; y -y ′; zz ′} ו- M ″ M = {x ″ -x ′; y ″ -y ′; z ″ -z ′} חייבים להיות קופלאניים עם הווקטור a = (a ′, a ″, a ‴), כלומר (M′M, M ″ M, a) = 0.
אז המשוואה שלנו של מטוס בחלל תיראה כך:
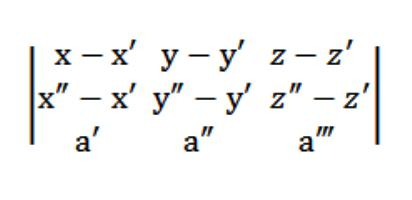
נניח שיש לנו שלוש נקודות:(x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴) שאינם שייכים לקו ישר אחד. יש צורך לכתוב את משוואת המטוס העובר בשלוש הנקודות הנתונות. תורת הגיאומטריה טוענת שמישור מסוג זה באמת קיים, אך רק הוא היחיד ובלתי אפשרי. מכיוון שמישור זה חותך את הנקודה (x ′, y ′, z ′), צורת המשוואה שלו תהיה כדלקמן:

כאן A, B, C הם אפס במקביל. כמו כן, המטוס הנתון חותך שתי נקודות נוספות: (x ″, y ″, z ″) ו- (x ‴, y ‴, z ‴). בהקשר זה, יש לעמוד בתנאים הבאים:

כעת נוכל לחבר מערכת הומוגנית של משוואות (לינאריות) עם u, v, w לא מוכרים:

במקרה שלנו, x, y או z הוא שרירותינקודה העונה למשוואה (1). בהתחשב במשוואה (1) ובמערכת המשוואות (2) ו- (3), מערכת המשוואות המצוינת באיור לעיל מתקבלת על ידי הווקטור N (A, B, C), שאינו טריוויאלי. לכן הקובע של מערכת זו שווה לאפס.
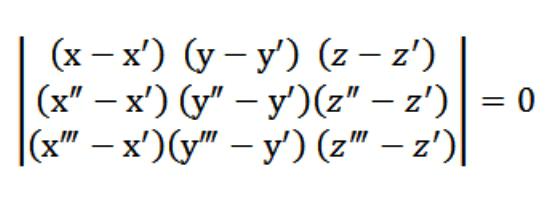
משוואה (1), שקיבלנו, היאהיא משוואת המטוס. הוא עובר 3 נקודות בדיוק, וקל לבדוק אותו. לשם כך עלינו להרחיב את הקובע שלנו על ידי האלמנטים הנמצאים בשורה הראשונה. מהמאפיינים הקיימים של הקובע עולה כי המטוס שלנו חותך בו זמנית שלוש נקודות שצוין בתחילה (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴) . כלומר, פתרנו את המשימה שהוצבה לפנינו.
הזווית הדיהידרלית היאדמות גיאומטרית מרחבית שנוצרה על ידי שני מטוסים חצי שיוצאים מקו ישר אחד. במילים אחרות, זהו חלק מהחלל המוגבל בחצי המישורים הללו.
נניח שיש לנו שני מישורים עם המשוואות הבאות:
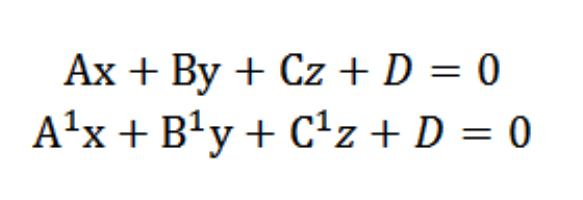
אנו יודעים כי הווקטורים N = (A, B, C) ו-N¹ = (A¹, B¹, C¹) הם בניצב בהתאם למישורים הנתונים. בהקשר זה, הזווית φ בין הווקטורים N ו- N¹ שוות לזווית (דו -הידרלית) הנמצאת בין המישורים הללו. מוצר הנקודה הוא:
NN¹ = | N || N¹ | cos φ,
בדיוק בגלל
cosφ = NN¹ / | N || N¹ | = (AA¹ + BB¹ + CC¹) / ((√ (A² + B² + C²)) * (√ (A¹) ² + (B¹) ² + (C¹) ²)).
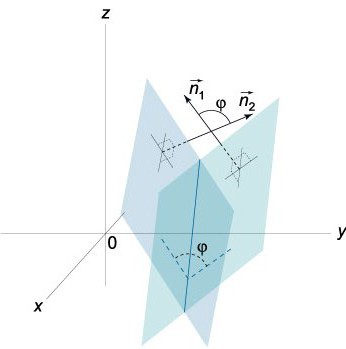
מספיק לקחת בחשבון ש 0≤φ≤π.
למעשה, שני מישורים המצטלבים יוצרים שתי זוויות (דידרה): φ1 ו- φ2... הסכום שלהם שווה ל- π (φ1+ φ2= π). באשר לקוסינוס שלהם, הערכים המוחלטים שלהם שווים, אך הם שונים בסימנים, כלומר cos φ1= -קוס φ2... אם במשוואה (0) נחליף את A, B ו- C במספרים -A, -B ו- -C, בהתאמה, אז המשוואה שאנו מקבלים תקבע את אותו המטוס, הזווית היחידה φ במשוואה cos φ = NN1/ | N || נ1| יוחלף ב- π-φ.
המטוסים נקראים בניצב, ביןאיזו זווית היא 90 מעלות. בעזרת החומר המתואר לעיל, נוכל למצוא את משוואת המטוס בניצב לאחר. נניח שיש לנו שני מישורים: Ax + By + Cz + D = 0 ו- A¹x + B¹y + C¹z + D = 0. אנו יכולים לטעון שהם יהיו בניצב אם cosφ = 0. המשמעות היא ש NN¹ = AA¹ + BB¹ + CC¹ = 0.
מקבילים הם שני מישורים שאינם מכילים נקודות משותפות.
התנאי לכך שהמטוסים יהיו מקבילים (משוואותיהםזהה לפרק הקודם) הוא שהווקטורים N ו- N¹, הניצבים אליהם, הם קולינאאריים. המשמעות היא שתנאי המידתיות הבאים מתקיימים:
A / A¹ = B / B¹ = C / C¹.
אם הורחבו תנאי המידתיות - A / A¹ = B / B¹ = C / C¹ = DD¹,
זה מצביע על כך שמישורים אלה חופפים. וזה אומר שהמשוואות Ax + By + Cz + D = 0 ו- A¹x + B¹y + C¹z + D¹ = 0 מתארות מישור אחד.
נניח שיש לנו מישור P, שהוא נתוןמשוואה (0). יש צורך למצוא את המרחק אליו מהנקודה עם קואורדינטות (xₒ, yₒ, zₒ) = Qₒ. לשם כך, עליך להביא את משוואת המטוס P לצורה רגילה:
(p, v) = p (p≥0).
במקרה זה ρ (x, y, z) הואוקטור הרדיוס של הנקודה שלנו Q, הממוקם על P, p הוא אורך ה- P הניצב, ששוחרר מנקודת האפס, v הוא וקטור היחידה, הממוקם בכיוון a.

ההבדל ρ-ρº של וקטור הרדיוס של נקודה כלשהי Q = (x, y, z), השייך ל- P, כמו גם וקטור הרדיוס של נקודה נתונה Q0= (xₒ, yₒ, zₒ) הוא וקטור כזה, שהערך המוחלט של ההקרנה שלו ב- v שווה למרחק d, אותו יש למצוא מ- Q0= (xₒ, yₒ, zₒ) ל- P:
D = | (ρ-ρ0, v) |, אבל
(ρ-ρ0, v) = (ρ, v) - (ρ0, v) = р– (ρ0, v).
אז מסתבר
d = | (ρ0, v) -p |.
כעת נראה לחישוב המרחק d מ- Q0 למישור P, עליך להשתמש בצורה הרגילה של משוואת המטוס, תוך העברה לצד השמאלי של p, ולהחליף (xₒ, yₒ, zₒ) האחרון במקום x, y, z.
לפיכך, נמצא את הערך המוחלט של הביטוי המתקבל, כלומר ה- d הרצוי.
בעזרת שפת הפרמטרים אנו מקבלים את המובן מאליו:
d = | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).
אם נקודה נתונה ש0 נמצא בצד השני של המטוס P, כמו המוצא, ואז בין הווקטור ρ-ρ0 ו- v היא זווית קהה, לכן:
d = - (ρ -ρ0, v) = (ρ0, v) -p> 0.
במקרה בו הנקודה ש0 יחד עם מקור הקואורדינטות ממוקם באותו צד של P, אז הזווית שנוצרת היא חריפה, כלומר:
d = (ρ-ρ0, v) = p - (עמ '0, v)> 0.
כתוצאה מכך, מסתבר שבמקרה הראשון (ρ0, v)> р, בשני (ρ0, v) <p.
המישור המשיק אל פני השטח בנקודת המשיק Mº הוא המישור המכיל את כל המשיקים האפשריים לעקומות שנמשכות דרך נקודה זו על פני השטח.
עם צורה זו של משוואת פני השטח F (x, y, z) = 0, המשוואה של המישור המשיק בנקודת המשיק Mº (xº, yº, zº) תיראה כך:
וx(xº, yº, zº) (x- xº) + Fx(xº, yº, zº) (y- yº) + Fx(xº, yº, zº) (z-zº) = 0.
אם נקבע את המשטח בצורה מפורשת z = f (x, y), אז המישור המשיק יתואר על ידי המשוואה:
z-zº = f (xº, yº) (x- xº) + f (xº, yº) (y-yº).
המערכת ממוקמת בחלל תלת מימדיקואורדינטות (מלבניות) Oxyz, שני מישורים P ′ ו- P ″ ניתנים, המצטלבים ואינם חופפים. מכיוון שכל מישור במערכת קואורדינטות מלבניות נקבע על ידי המשוואה הכללית, נניח כי P ′ ו- P ″ ניתנות על ידי המשוואות Ax + B′y + C′z + D ′ = 0 ו- A ″ x + B ″ y + C ″ z + D ″ = 0. במקרה זה, יש לנו את ה- n ′ (A ′, B ′, C ′) הנורמלי של המטוס P ′ ואת ה- N normal (A ″, B ″, C ″) הרגיל של המטוס P ″. מכיוון שהמטוסים שלנו אינם מקבילים ואינם חופפים, הווקטורים הללו אינם קולינאריים. בעזרת שפת המתמטיקה נוכל לכתוב מצב זה כדלקמן: n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. תן לקו הישר שנמצא בצומת P ′ ו- P be יצוין באות a, במקרה זה a = P ′ ∩ P ″.
a הוא קו ישר המורכב ממכלול כל הנקודותמטוסים (נפוצים) P ′ ו- P ″. המשמעות היא שהקואורדינטות של כל נקודה השייכת לקו הישר a חייבות במקביל לספק את המשוואות A'x + B'y + C'z + D '= 0 ו- A ″ x + B ″ y + C ″ z + D ″ = 0. המשמעות היא שקואורדינטות הנקודה יהיו פתרון מסוים של מערכת המשוואות הבאה:

כתוצאה מכך, מתברר כי הפתרון (הכללי) של זהמערכת המשוואות תקבע את הקואורדינטות של כל אחת מנקודות הקו הישר, אשר תפעל כנקודת החיתוך של P ′ ו- P ″, ותקבע את הקו הישר a במערכת הקואורדינטות Oxyz (מלבנית) בחלל.


























